Handling parallels after getting a path (pgr_ksp focus)¶
| Author: | pgRouting team. |
|---|---|
| Licence: | Open Source |
The graph
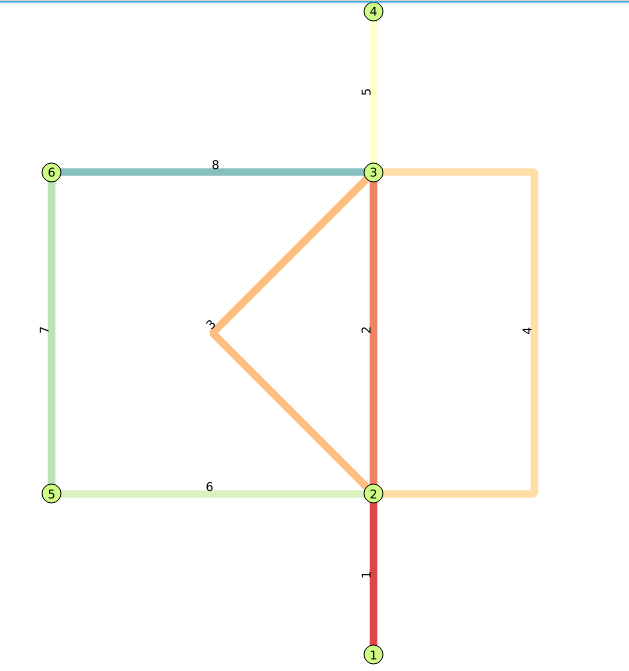
Data
drop table if exists parallel;
CREATE TABLE parallel (
id serial,
source integer,
target integer,
cost double precision,
reverse_cost double precision,
x1 double precision,
y1 double precision,
x2 double precision,
y2 double precision,
the_geom geometry
);
INSERT INTO parallel (x1,y1,x2,y2)
VALUES (1,0,1,1),(1,1,1,3),(1,1,1,3),(1,1,1,3),(1,3,1,4),(1,1,-1,1),(-1,1,-1,3),(-1,3,1,3);
UPDATE parallel SET the_geom = ST_makeline(ST_point(x1,y1),ST_point(x2,y2));
UPDATE parallel SET the_geom = ST_makeline(ARRAY[ST_point(1,1),ST_point(0,2),ST_point(1,3)]) WHERE id = 3;
UPDATE parallel SET the_geom = ST_makeline(ARRAY[ST_point(1,1),ST_point(2,1),ST_point(2,3),ST_point(1,3)])
WHERE id = 4;
UPDATE parallel SET cost = ST_length(the_geom), reverse_cost = ST_length(the_geom);
SELECT pgr_createTopology('parallel',0.001);
pgr_ksp results
We ignore the costs because we want all the parallels
SELECT seq, path_id AS route, node, edge INTO routes
from pgr_ksp('select id, source, target, cost, reverse_cost from parallel',
1, 4, 3);
select route, node, edge from routes;
route | node | edge
-------+------+------
1 | 1 | 1
1 | 2 | 2
1 | 3 | 5
1 | 4 | -1
2 | 1 | 1
2 | 2 | 6
2 | 5 | 7
2 | 6 | 8
2 | 3 | 5
2 | 4 | -1
(10 rows)
We need an aggregate function:
CREATE AGGREGATE array_accum (anyelement)
(
sfunc = array_append,
stype = anyarray,
initcond = '{}'
);
Now lets generate a table with the parallel edges.
select distinct seq,route,source,target, array_accum(id) as edges into paths
from (select seq, route, source, target
from parallel, routes where id = edge) as r
join parallel using (source, target)
group by seq,route,source,target order by seq;
select route, source, targets, edges from paths;
route | source | target | edges
-------+--------+--------+---------
1 | 1 | 2 | {1}
2 | 1 | 2 | {1}
2 | 2 | 5 | {6}
1 | 2 | 3 | {2,3,4}
2 | 5 | 6 | {7}
1 | 3 | 4 | {5}
2 | 6 | 3 | {8}
2 | 3 | 4 | {5}
(8 rows)
Some more aggregate functions
To generate a table with all the combinations for parallel routes, we need some more aggregates
create or replace function multiply( integer, integer )
returns integer as
$$
select $1 * $2;
$$
language sql stable;
create aggregate prod(integer)
(
sfunc = multiply,
stype = integer,
initcond = 1
);
And a function that “Expands” the table
CREATE OR REPLACE function expand_parallel_edge_paths(tab text)
returns TABLE (
seq INTEGER,
route INTEGER,
source INTEGER, target INTEGER, -- this ones are not really needed
edge INTEGER ) AS
$body$
DECLARE
nroutes INTEGER;
newroutes INTEGER;
rec record;
seq2 INTEGER := 1;
rnum INTEGER := 0;
BEGIN -- get the number of distinct routes
execute 'select count(DISTINCT route) from ' || tab INTO nroutes;
FOR i IN 0..nroutes-1
LOOP
-- compute the number of new routes this route will expand into
-- this is the product of the lengths of the edges array for each route
execute 'select prod(array_length(edges, 1))-1 from '
|| quote_ident(tab) || ' where route=' || i INTO newroutes;
-- now we generate the number of new routes for this route
-- by repeatedly listing the route and swapping out the parallel edges
FOR j IN 0..newroutes
LOOP
-- query the specific route
FOR rec IN execute 'select * from ' || quote_ident(tab) ||' where route=' || i
|| ' order by seq'
LOOP
seq := seq2;
route := rnum;
source := rec.source;
target := rec.target;
-- using module arithmetic iterate through the various edge choices
edge := rec.edges[(j % (array_length(rec.edges, 1)))+1];
-- return a new record
RETURN next;
seq2 := seq2 + 1; -- increment the record count
END LOOP;
seq := seq2;
route := rnum;
source := rec.target;
target := -1;
edge := -1;
RETURN next; -- Insert the ending record of the route
seq2 := seq2 + 1;
rnum := rnum + 1; -- increment the route count
END LOOP;
END LOOP;
END;
$body$
language plpgsql volatile strict cost 100 rows 100;
Test it
select * from expand_parallel_edge_paths( 'paths' );
seq | route | source | target | edge
-----+-------+--------+--------+------
1 | 0 | 1 | 2 | 1
2 | 0 | 2 | 3 | 2
3 | 0 | 3 | 4 | 5
4 | 0 | 4 | -1 | -1
5 | 1 | 1 | 2 | 1
6 | 1 | 2 | 3 | 3
7 | 1 | 3 | 4 | 5
8 | 1 | 4 | -1 | -1
9 | 2 | 1 | 2 | 1
10 | 2 | 2 | 3 | 4
11 | 2 | 3 | 4 | 5
12 | 2 | 4 | -1 | -1
13 | 3 | 1 | 2 | 1
14 | 3 | 2 | 5 | 6
15 | 3 | 5 | 6 | 7
16 | 3 | 6 | 3 | 8
17 | 3 | 3 | 4 | 5
18 | 3 | 4 | -1 | -1
(18 rows)
