pgRouting Manual (2.2)

Contraction

«  Contraction   ::   Contents   ::   pgr_vrpOneDepot  »

Contraction

Contracting a graph becomes a crucial operation when talking about big graphs like the graphs involved in routing across cities, countries, continents or the whole world.

The contraction level and contraction operations can become very complex, as the complexity of the graphs grows.

For this proposal, we are making our contraction algorithm simple as possible so that more contraction operations can be added in the future.

We are not aiming with this work to implement all the possible contraction operations but to give a framework such that adding a contraction operation can be easily achieved.

For this contraction proposal I am only making 2 operations:

  1. dead end contraction: vertices have one incoming edge
  2. linear contraction: vertices have one incomming and one outgoing edge

And with the additional characteristics:

  • The user can forbid to contract a particular set of nodes or edges.
  • The user can decide how many times the cycle can be done.
  • If possible, the user can decide the order of the operations on a cycle.

Note

Work on progress in contraction branch

The contraction skeleton

In general we have an initial set up that may involve analizing the graph given as input and setting the non contractable nodes or edges. We have a cycle that will go and perform a contraction operation until while possible, and then move to the next contraction operation. Adding a new operation then becomes an “easy” task; more things might be involved, because the charachteristics of the graph change each time its contracted, so some interaction between contractions has to be implemented also.

Procedure

  • For contracting, we are going to cycle as follows
input: G(V,E);
removed_vertices = {};


<initial set up>
do N times {

    while ( <conditions for 1> ) {
        < contraction operation 1 >
    }

    while ( <conditions for 2> ) {
        < contraction operation 2>
    }
    .....
}

output: G'(V',E'), removed_vertices

Contraction operations for this implementation

Dead end contraction

Characteristics:

  • \(V1\): set of vertices with 1 incoming edge in increasing order of id:
    • Edges with the same identifier are considered the same edge and if it has the reverse_cost valid the outgoing edge is ignored
while ( V1 is not empty ) {

    delete vertex of V1
    the deleted vertex add it to removed_vertices
    vertex that leads to removed vertex, inherits the removed vertex

    <adjust any conditions that might affect other contraction operation>
}

Linear contraction

Characteristics:

  • \(V2\): vertex with 1 incoming edge and 1 outgoing edge:
    • The outgoing edge must have different identifier of the incomming edge
while ( V2 is not empty ) {

    delete vertex of V2
    create edge (shortcut)
    the deleted vertex add it to removed_vertices
    inewly created edge, inherits the removed vertex

    <adjust any conditions that might affect other contraction operations>
}

Notation

  • V: is the set of vertices
  • E: is the set of edges
  • G: is the graph
  • \(V1\): is the set of dead end vertices
  • \(V2\): is the set of linear vertices
  • removed_vertices: is the set of removed vertices

The contracted graph will be represented with two parameters, the modified Graph, and the removed_vertices set.

removed_vertices = {(v,1):{2}, (e,-1):{3}}.

The above notation indicates:
  • Vertex 2 is removed, and belongs to vertex 1 subgraph
  • Vertex 3 is removed, and belongs to edge -1 subgraph

Examples

For simplicity all the edges in the examples have unit weight.

Dead End

  • Perform dead end contraction operation first and then linear contraction
  • 1 cycle of contraction.
../../../_images/twoNodesoneEdge_a.png
Input:G = {V:{1, 2}, E:{(1, 2)}}
initial set up: 
removed_vertices={}
V1 = {2}
V2 = {}
procedure: 
V1 = {2} is not empty

    V1 = {}
    V2 = {}
    G = {V:{1}, E:{}}
    removed_vertices = {(v, 1):{2}}.

V1 is empty

Since V1 is empty we go on to the next contraction operation

V2 is empty

So we do not perform any linear contraction operation.

Results: 
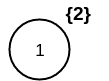
G = {V:{1}, E:{}}
removed_vertices = {(v, 1):{2}}

Visualy the results are

../../../_images/twoNodesoneEdge_b.png

Linear contraction

  • Perform linear contraction operation first and then dead end contraction
  • 1 cycle of contraction.
../../../_images/threeNodestwoEdges_a.png
Input:G = {V:{1, 2, 3}, E:{(1, 2), (2, 3)}}
initial set up: 
removed_vertices={}
V1 = {3}
V2 = {2}
procedure: 
V2 = {2} is not empty

    V1 = {3}
    removed_vertices = {(e, -1):{2}}
    V2 = {}
    G = {V:{1, 3}, E:{-1(1,3,c=2)}}

V2 is empty
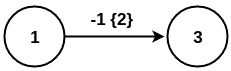
../../../_images/threeNodestwoEdges_b.png

Since V2 is empty we go on to the next contraction operation

V1 = {3} is not empty

    V1 = {}
    V2 = {}
    removed_vertices = {(v, 1):{3, 2}}.
    G = {V:{1}, E:{}}

V1 is empty
Results: 
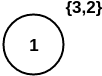
removed_vertices = {(v, 1):{3, 2}}.
G = {V:{1}, E:{}}

Visualy the results are

../../../_images/threeNodestwoEdges_c.png

Sample Data

  • Perform dead end contraction operation first and then linear contraction
  • 1 cycle of contraction.
../../../_images/undirected_sampledata_a.png
Input:G = {V:{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17}, E:{1(1, 2), 2(2,3), 3(3,4), 4(2,5), 5(3,6), 6(7,8), 7(8,5), 8(5,6), 9(6,9), 10(5,10), 11(6,11), 12(10,11), 13(11,12), 14(10,13), 15(9,12), 16(4,9), 17(14,15), 18(16,17)}}
initial set up: 
removed_vertices={}
V1 = {1,7,13,14,15,16,17}
V2 = {4,8,12}
procedure: 
V1 = {1,7,13,14,15,16,17} is not empty

    V1 = {7,13,14,15,16,17}
    V2 = {2,4,8,12}
    G = {V:{2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17},
    E:{2(2,3), 3(3,4), 4(2,5), 5(3,6), 6(7,8), 7(8,5), 8(5,6), 9(6,9),
        10(5,10), 11(6,11), 12(10,11), 13(11,12), 14(10,13), 15(9,12), 16(4,9), 17(14,15), 18(16,17)}}
    removed_vertices = {(v, 2):{1}}.


V1 = {7,13,14,15,16,17} is not empty

    V1 = {8,13,14,15,16,17}
    V2 = {2,4,12}
    G = {V:{2, 3, 4, 5, 6, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17},
    E:{2(2,3), 3(3,4), 4(2,5), 5(3,6), 7(8,5), 8(5,6), 9(6,9), 10(5,10),
        11(6,11), 12(10,11), 13(11,12), 14(10,13), 15(9,12), 16(4,9), 17(14,15), 18(16,17)}}
    removed_vertices = {(v, 2):{1}, (v,8):{7}}.

V1 = {8,13,14,15,16,17} is not empty

    V1 = {13,14,15,16,17}
    V2 = {2,4,12}
    G = {V:{2, 3, 4, 5, 6, 9, 10, 11, 12, 13, 14, 15, 16, 17},
    E:{2(2,3), 3(3,4), 4(2,5), 5(3,6), 8(5,6), 9(6,9), 10(5,10),
         11(6,11), 12(10,11), 13(11,12), 14(10,13), 15(9,12), 16(4,9), 17(14,15), 18(16,17)}}
    removed_vertices = {(v, 2):{1}, (v,5):{8,7}}.

V1 = {13,14,15,16,17} is not empty

    V1 = {14,15,16,17}
    V2 = {2,4,10,12}
    G = {V:{2, 3, 4, 5, 6, 9, 10, 11, 12, 14, 15, 16, 17},
    E:{2(2,3), 3(3,4), 4(2,5), 5(3,6), 8(5,6), 9(6,9), 10(5,10),
         11(6,11), 12(10,11), 13(11,12), 15(9,12), 16(4,9), 17(14,15), 18(16,17)}}
    removed_vertices = {(v, 2):{1}, (v,5):{8,7}, (v,10):{13}}.

V1 = {14,15,16,17} is not empty

    V1 = {16,17}
    V2 = {2,4,10,12}
    G = {V:{2, 3, 4, 5, 6, 9, 10, 11, 12, 15, 16, 17},
    E:{2(2,3), 3(3,4), 4(2,5), 5(3,6), 8(5,6), 9(6,9), 10(5,10),
         11(6,11), 12(10,11), 13(11,12), 15(9,12), 16(4,9)}, 18(16,17)}
    removed_vertices = {(v, 2):{1}, (v,5):{8,7}, (v,10):{13}, (v,15):{14}}.

V1 = {16,17} is not empty

    V1 = {}
    V2 = {2,4,10,12}
    G = {V:{2, 3, 4, 5, 6, 9, 10, 11, 12, 15, 17},
    E:{2(2,3), 3(3,4), 4(2,5), 5(3,6), 8(5,6), 9(6,9), 10(5,10),
         11(6,11), 12(10,11), 13(11,12), 15(9,12), 16(4,9)}}
    removed_vertices = {(v, 2):{1}, (v,5):{8,7}, (v,10):{13}, (v,15):{14}, (v,17):{16}}.

Since V1 is empty we go on to the next contraction operation
../../../_images/undirected_sampledata_b.png 
V2 = {2,4,10,12} is not empty

    V1 = {}
    V2 = {4,10,12}
    G = {V:{3, 4, 5, 6, 9, 10, 11, 12, 15, 17},
    E:{-1(3,5), 3(3,4), 5(3,6), 8(5,6), 9(6,9), 10(5,10),
         11(6,11), 12(10,11), 13(11,12), 15(9,12), 16(4,9)}}
    removed_vertices = {(e, -1):{1,2}, (v, 2):{1}, (v,5):{8,7}, (v,10):{13}, (v,15):{14}, (v,17):{16}}.

V2 = {4,10,12} is not empty

    V1 = {}
    V2 = {10,12}
    G = {V:{3, 5, 6, 9, 10, 11, 12, 15, 17},
    E:{-1(3,5),-2(3,9), 5(3,6), 8(5,6), 9(6,9), 10(5,10),
         11(6,11), 12(10,11), 13(11,12), 15(9,12)}}
    removed_vertices = {(e, -1):{1,2}, (e, -2):{4}, (v, 2):{1}, (v,5):{8,7}, (v,10):{13}, (v,15):{14}, (v,17):{16}}.

V2 = {10,12} is not empty

    V1 = {}
    V2 = {12}
    G = {V:{3, 5, 6, 9, 11, 12, 15, 17},
    E:{-1(3,5),-2(3,9), -3(5,11), 5(3,6), 8(5,6), 9(6,9),
         11(6,11), 13(11,12), 15(9,12)}}
    removed_vertices = {(e, -1):{1,2}, (e, -2):{4}, (e,-3):{10,13}, (v, 2):{1}, (v,5):{8,7}, (v,15):{14}, (v,17):{16}}.

V2 = {12} is not empty

    V1 = {}
    V2 = {}
    G = {V:{3, 5, 6, 9, 11, 15, 17},
    E:{-1(3,5),-2(3,9), -3(5,11), -4(9,11), 5(3,6), 8(5,6), 9(6,9), 11(6,11)}}
    removed_vertices = {(e, -1):{1,2}, (e, -2):{4}, (e,-3):{10,13}, (e, -4):{12},
         (v, 2):{1}, (v,5):{8,7}, (v,15):{14}, (v,17):{16}}.

Since V1 and V2 are empty we stop our contraction here.

Results: 
G = {V:{3, 5, 6, 9, 11, 15, 17},
E:{-1(3,5),-2(3,9), -3(5,11), -4(9,11), 5(3,6), 8(5,6), 9(6,9), 11(6,11)}}
removed_vertices = {(e, -1):{1,2}, (e, -2):{4}, (e,-3):{10,13}, (e, -4):{12},
     (v, 2):{1}, (v,5):{8,7}, (v,15):{14}, (v,17):{16}}.

Visualy the results are

../../../_images/undirected_sampledata_c.png

«  Contraction   ::   Contents   ::   pgr_vrpOneDepot  »

© Copyright pgRouting Contributors - Version 2.2.4 (pgrouting-2.2.4). Last updated on Aug 09, 2016. Created using Sphinx 1.2.2.