Unsupported versions:2.6 2.5 2.4 2.3 2.2
withPoints - Family of functions¶
When points are also given as input:
- pgr_withPoints - Proposed - Route from/to points anywhere on the graph.
- pgr_withPointsCost - Proposed - Costs of the shortest paths.
- pgr_withPointsCostMatrix - proposed - Costs of the shortest paths.
- pgr_withPointsKSP - Proposed - K shortest paths.
- pgr_withPointsDD - Proposed - Driving distance.
Warning
These are proposed functions for next mayor release.
- They are not officially in the current release.
- They will likely officially be part of the next mayor release:
- The functions make use of ANY-INTEGER and ANY-NUMERICAL
- Name might not change. (But still can)
- Signature might not change. (But still can)
- Functionality might not change. (But still can)
- pgTap tests have being done. But might need more.
- Documentation might need refinement.
Images¶
The squared vertices are the temporary vertices, The temporary vertices are added acordng to the dirving side, The following images visualy show the diferences on how depending on the driving side the data is interpreted.
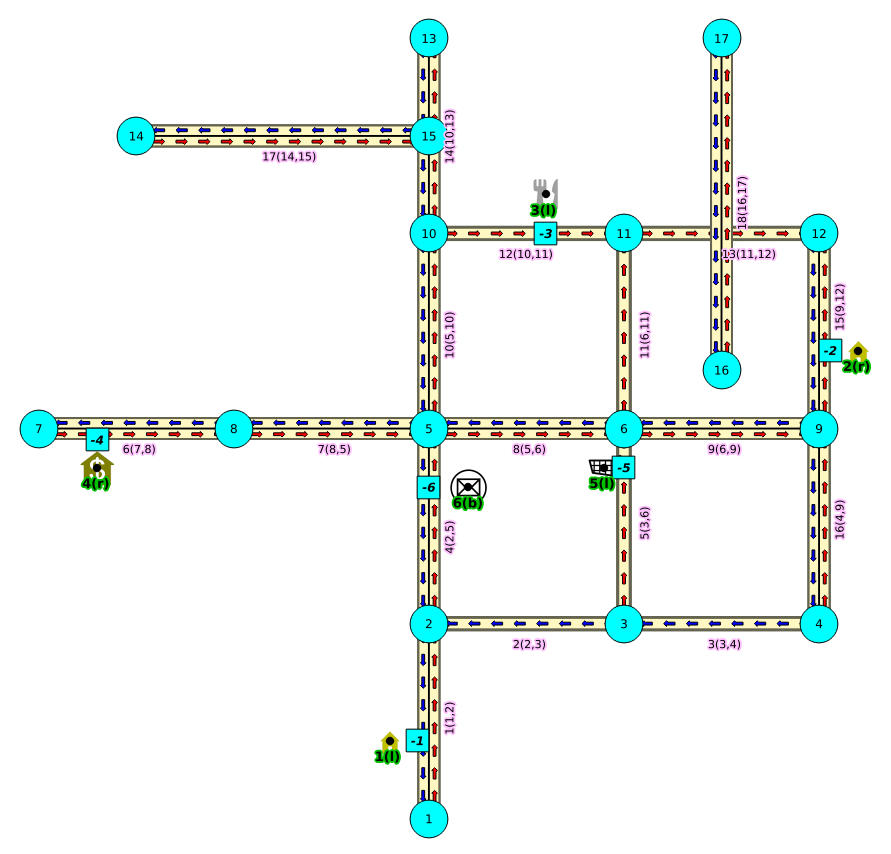
Right driving side
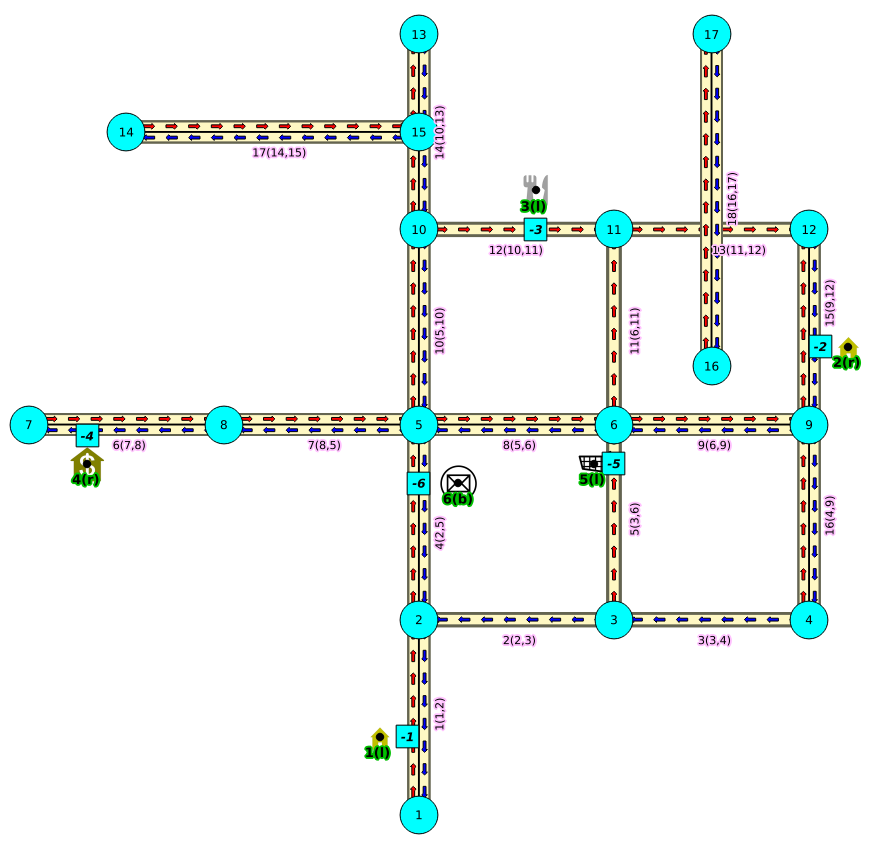
Left driving side
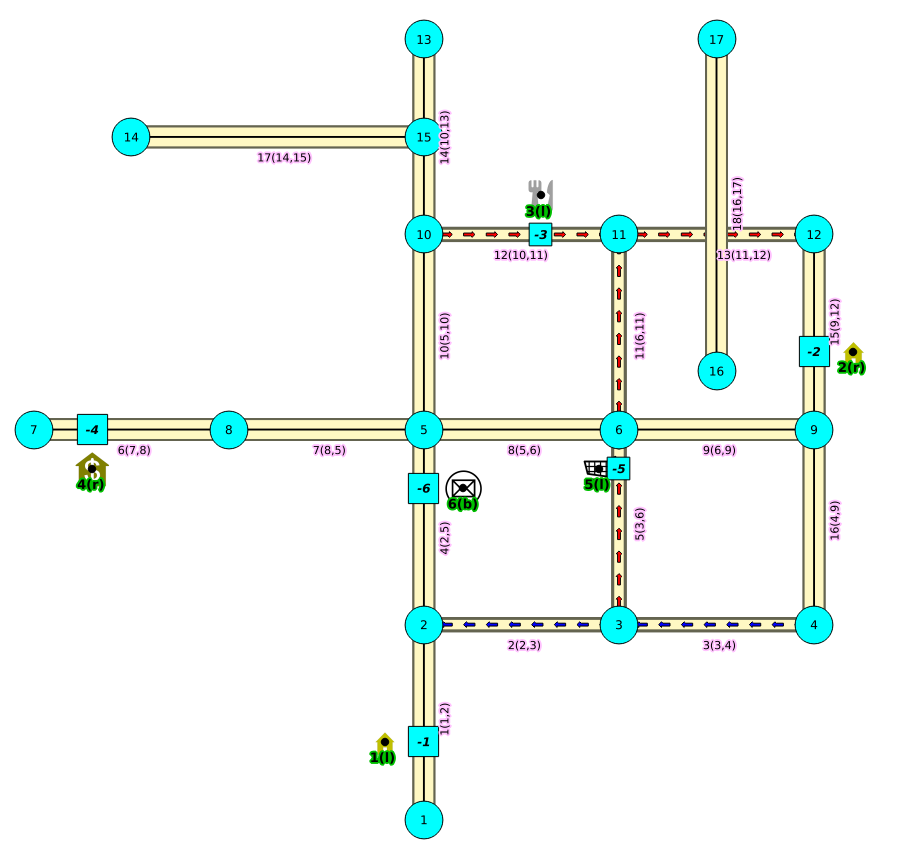
doesn’t matter the driving side
Introduction¶
This famly of functions was thought for routing vehicles, but might as well work for some other application that we can not think of.
The with points family of function give you the ability to route between arbitrary points located outside the original graph.
When given a point identified with a pid that its being mapped to and edge with an identifier edge_id, with a fraction along that edge (from the source to the target of the edge) and some additional information about which side of the edge the point is on, then routing from arbitrary points more accurately reflect routing vehicles in road networks,
- I talk about a family of functios because it includes different functionalities.
- pgr_withPoints is pgr_dijkstra based
- pgr_withPointsCost is pgr_dijkstraCost based
- pgr_withPointsKSP is pgr_ksp based
- pgr_withPointsDD is pgr_drivingDistance based
In all this functions we have to take care of as many aspects as possible:
Must work for routing:
- Cars (directed graph)
- Pedestrians (undirected graph)
Arriving at the point:
- In either side of the street.
- Compulsory arrival on the side of the street where the point is located.
Countries with:
- Right side driving
- Left side driving
Some points are:
- Permanent, for example the set of points of clients stored in a table in the data base
- Temporal, for example points given through a web application
The numbering of the points are handled with negative sign.
- Original point identifiers are to be positive.
- Transformation to negative is done internally.
- For results for involving vertices identifiers
- positive sign is a vertex of the original grpah
- negative sign is a point of the temporary points
The reason for doing this is to avoid confusion when there is a vertex with the same number as identifier as the points identifier.
Graph & edges¶
- Let Gd(V,E) where V is the set of vertices and E is the set of edges be the original directed graph.
- An edge of the original edges_sql is (id,source,target,cost,reverse_cost) will generate internally
- (id,source,target,cost)
- (id,target,source,reverse_cost)
- An edge of the original edges_sql is (id,source,target,cost,reverse_cost) will generate internally
Point Definition¶
A point is defined by the quadruplet: (pid,eid,fraction,side)
ped: is the point identifier eid: is an edge id of the edges_sql fraction: represents where the edge eid will be cut. side: Indicates the side of the edge where the point is located.
Creating Temporary Vertices in the Graph¶
For edge (15, 9,12 10, 20), & lets insert point (2, 12, 0.3, r)
On a right hand side driving network
From first image above:
- We can arrive to the point only via vertex 9.
- It only afects the edge (15, 9,12, 10) so that edge is removed.
- Edge (15, 12,9, 20) is kept.
- Create new edges:
- (15, 9,-1, 3) edge from vertex 9 to point 1 has cost 3
- (15, -1,12, 7) edge from point 1 to vertex 12 has cost 7
On a left hand side driving network
From second image above:
- We can arrive to the point only via vertex 12.
- It only afects the edge (15, 12,9 20) so that edge is removed.
- Edge (15, 9,12, 10) is kept.
- Create new edges:
- (15, 12,-1, 14) edge from vertex 12 to point 1 has cost 14
- (15, -1,9, 6) edge from point 1 to vertex 9 has cost 6
| Remember: | that fraction is from vertex 9 to vertex 12 |
|---|
When driving side does not matter
From third image above:
- We can arrive to the point either via vertex 12 or via vertex 9
- Edge (15, 12,9 20) is removed.
- Edge (15, 9,12, 10) is removed.
- Create new edges:
- (15, 12,-1, 14) edge from vertex 12 to point 1 has cost 14
- (15, -1,9, 6) edge from point 1 to vertex 9 has cost 6
- (15, 9,-1, 3) edge from vertex 9 to point 1 has cost 3
- (15, -1,12, 7) edge from point 1 to vertex 12 has cost 7
