pgr_lineGraphFull - Experimental¶

pgr_lineGraphFull — Transforma un grafo dado en uno nuevo donde todos los vértices del grafo original se convierten en grafos de líneas.

Advertencia

Posible bloqueo del servidor

Estas funciones pueden crear un bloqueo del servidor

Advertencia

Funciones experimentales

No son oficialmente de la versión actual.
Es probable que oficialmente no formen parte de la siguiente versión:
- Las funciones no podrían hacer uso de ANY-INTEGER ni ANY-NUMERICAL
- El nombre puede cambiar.
- La firma (declaración de funciones) podría cambiar.
- La funcionalidad puede cambiar.
- Las pruebas de pgTap pueden estar ausentes.
- Posiblemente necesite codificación c/c++.
- Puede haber carencia de documentación.
- Hay documentación que, en dado caso, podría ser necesario reescribir.
- Ejemplos de documentación que puede ser necesario generar automáticamente.
- Puede ser necesaria más retroalimentación por parte de la comunidad.
- Puede depender de una función propuesta de pgRouting.
- Podría depender de una función obsoleta de pgRouting

Disponibilidad

Versión 2.6.0
- Nueva función Experimental

Soporte

Descripción¶

pgr_lineGraphFull, convierte un grafo dirigido original a un grafo lineal dirigido, convirtiendo cada vértice en un grafo completo y manteniendo todas las aristas originales. Las nuevas aristas de conexión tienen un costo de 0 y van entre las aristas originales adyacentes, respetando la direccionalidad.

Una posible aplicación del grafo resultante es «ruteo con restricciones en dos aristas»:

Establecer un coste de uso del vértice al enrutar entre aristas en la arista de conexión
Prohibir el ruteo entre dos aristas al quitar el arista de conexión

Esto es posible porque cada una de las intersecciones (vértices) en el grafo original ahora son grafos completos que tienen una nueva arista para cada posible giro a través de esa intersección.

Las principales características son:

Esta función es para grafos dirigidos.
Los resultados son indefinidos cuando se utiliza un identificador de vértice negativo en el grafo de entrada.
Los resultados son indefinidos cuando se utiliza un identificador de borde duplicado en el grafo de entrada.
Tiempo de ejecución: TBD

Firmas¶

Resumen

pgr_lineGraphFull(edges_sql)
RETURNS SET OF (seq, source, target, cost, edge)
    OR EMPTY SET

Uso de valores predeterminados

pgr_lineGraphFull(TEXT edges_sql)
RETURNS SET OF (seq, source, target, cost, edge) OR EMPTY SET

Ejemplo:	Grafo de línea completa del subgrafo de las aristas \(\{4, 7, 8, 10\}\)

SELECT * FROM pgr_lineGraphFull(
    'SELECT id, source, target, cost, reverse_cost
      FROM edge_table
      WHERE id IN (4,7,8,10)'
);
 seq | source | target | cost | edge
-----+--------+--------+------+------
|     -1 |      5 |    1 |    4
|      2 |     -1 |    0 |    0
|     -2 |      2 |    1 |   -4
|     -3 |      8 |    1 |   -7
|     -4 |      6 |    1 |    8
|     -5 |     10 |    1 |   10
|      5 |     -2 |    0 |    0
|      5 |     -3 |    0 |    0
|      5 |     -4 |    0 |    0
|      5 |     -5 |    0 |    0
|     -6 |     -2 |    0 |    0
|     -6 |     -3 |    0 |    0
|     -6 |     -4 |    0 |    0
|     -6 |     -5 |    0 |    0
|     -7 |     -2 |    0 |    0
|     -7 |     -3 |    0 |    0
|     -7 |     -4 |    0 |    0
|     -7 |     -5 |    0 |    0
|     -8 |     -2 |    0 |    0
|     -8 |     -3 |    0 |    0
|     -8 |     -4 |    0 |    0
|     -8 |     -5 |    0 |    0
|     -9 |     -6 |    1 |    7
|      8 |     -9 |    0 |    0
|    -10 |     -7 |    1 |   -8
|      6 |    -10 |    0 |    0
|    -11 |     -8 |    1 |  -10
|     10 |    -11 |    0 |    0
(28 rows)

Parámetros¶

Columna	Tipo	Valores predeterminados	Descripción
sql	`TEXT`		Consulta SQL como se describió anteriormente.

Consulta interna¶

Columna	Tipo	Valores predeterminados	Descripción
id	`ANY-INTEGER`		Identificador de la arista.
origen	`ANY-INTEGER`		Identificador del primer punto final en el vértice de la arista.
objetivo	`ANY-INTEGER`		Identificador del segundo punto final en el vértice de la arista.
cost	`ANY-NUMERICAL`		Peso de la arista (source, target) Cuando es negativo: la arista (source, target) no existe, por lo tanto no es parte del grafo.
reverse_cost	`ANY-NUMERICAL`	-1	Peso de la arista (target, source), En caso negativo: la arista (target, source) no existe, por lo tanto no es parte del grafo.

Donde:

ANY-INTEGER:	SMALLINT, INTEGER, BIGINT
ANY-NUMERICAL:	SMALLINT, INTEGER, BIGINT, REAL, FLOAT

Ejemplos Adicionales¶

Los ejemplos de esta sección se basan en la red Datos Muestra.

Los ejemplos incluyen el subgrafo que incluye las aristas 4, 7, 8 y 10 con reverse_cost.

Ejemplo:	Por generar el LineGraphFull

En este ejemplo se muestra cómo funciona esta transformación de grafo para crear aristas adicionales para cada giro posible en un grafoáfico.

SELECT id, source, target, cost, reverse_cost
  FROM edge_table
  WHERE id IN (4,7,8,10);

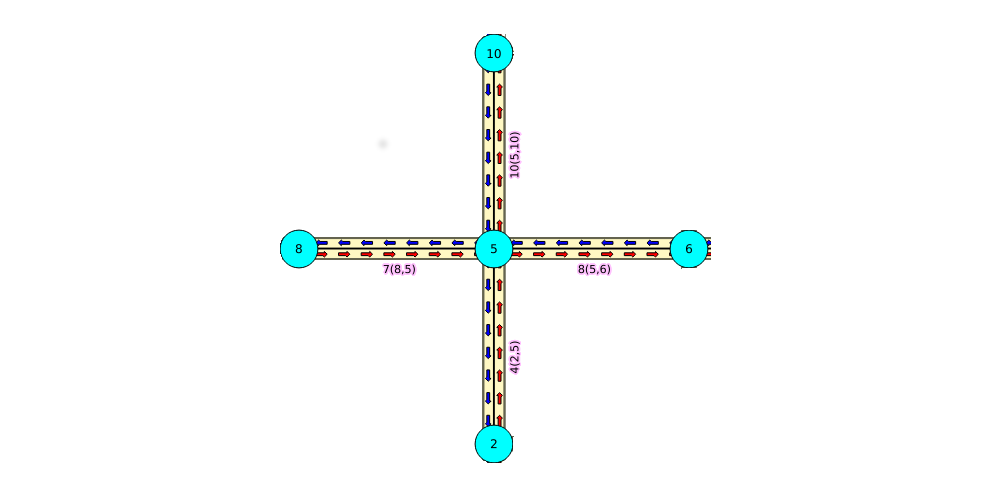
SELECT * FROM pgr_lineGraphFull('SELECT id,
                                        source,
                                        target,
                                        cost,
                                        reverse_cost
                                   FROM edge_table
                                     WHERE id IN (4,7,8,10)');

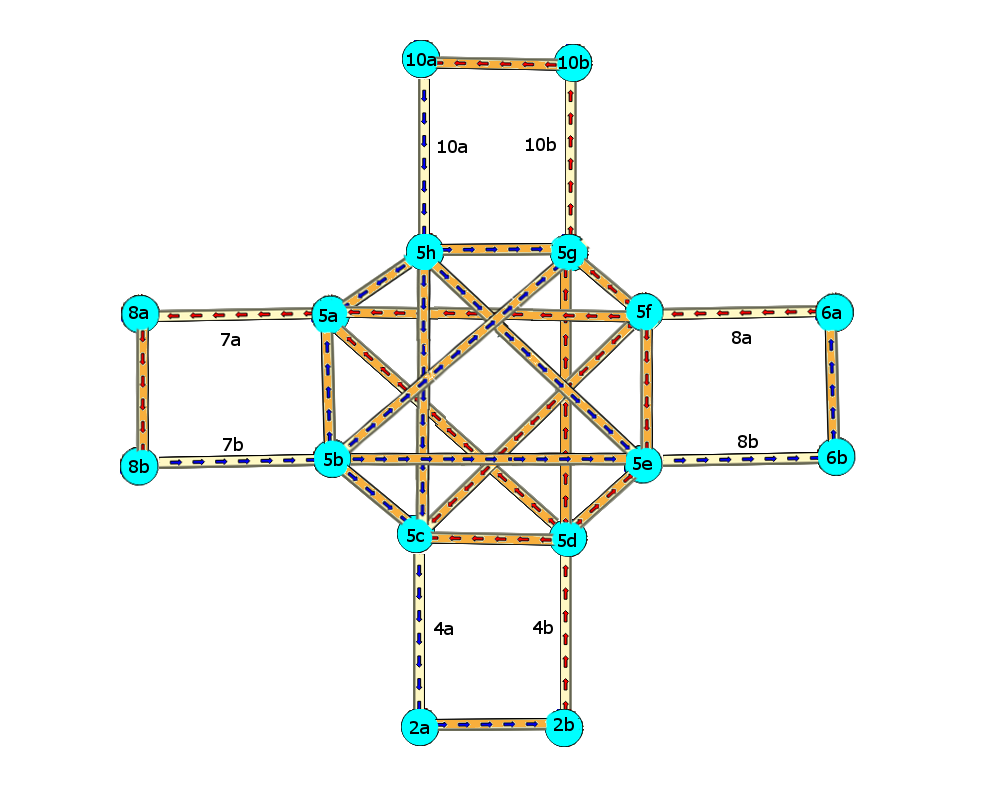
En el grafo transformado, todas las aristas del grafo original siguen presentes (amarillos), pero ahora tenemos aristas adicionales para cada giro que se podría hacer a través del vértice 6 (naranja).

Ejemplo:	Para crear una tabla que identifique vértices transformados

Los vértices del grafo transformado se crean dividiendo los vértices en el grafo original. A menos que un vértice en el grafo original sea un vértice de hoja, generará más de un vértice en el grafo transformado. A uno de los vértices recién creados en el grafo transformado se le dará el mismo vértice-id que el vértice desde el que se creó en el grafo original, pero el resto de los vértices recién creados tendrán identificadores de vértices negativos. A continuación se muestra un ejemplo de cómo generar una tabla que mapea los identificadores de los vértices recién creados con el vértice original que se crearon a partir de

El primer paso es almacenar el grafo de resultados en una tabla y, a continuación, crear la tabla de asignación de vértices con una fila para cada identificador de vértice distinto en el grafo resultante.

CREATE TABLE lineGraph_edges AS SELECT * FROM pgr_lineGraphFull(
    $$SELECT id, source, target, cost, reverse_cost
    FROM edge_table WHERE id IN (4,7,8,10)$$
);
SELECT 28
CREATE TABLE lineGraph_vertices AS
SELECT *, NULL::BIGINT AS original_id
FROM (SELECT source AS id FROM lineGraph_edges
    UNION
    SELECT target FROM lineGraph_edges) as foo
ORDER BY id;
SELECT 16

A continuación, establecemos el original_id de todos los vértices en el grafo de resultados a los que se les dio el mismo identificador de vértice que el vértice desde el que se creó en el grafo original.

UPDATE lineGraph_vertices AS r
  SET original_id = v.id
  FROM edge_table_vertices_pgr AS v
  WHERE v.id = r.id;
UPDATE 5

A continuación, cruzamos la referencia a todos los otros vértices recién creados que no tienen el mismo original_id y establecemos sus valores original_id.

WITH
unassignedVertices
  AS (SELECT e.id, e.original_id
       FROM lineGraph_vertices AS e
       WHERE original_id IS NOT NULL),
edgesWithUnassignedSource
  AS (SELECT *
        FROM lineGraph_edges
        WHERE cost = 0 and source IN (SELECT id FROM unassignedVertices)),
edgesWithUnassignedSourcePlusVertices
  AS (SELECT *
        FROM edgesWithUnassignedSource
        JOIN lineGraph_vertices
        ON(source = id)),
verticesFromEdgesWithUnassignedSource
  AS (SELECT DISTINCT edgesWithUnassignedSourcePlusVertices.target,
                      edgesWithUnassignedSourcePlusVertices.original_id
        FROM edgesWithUnassignedSourcePlusVertices
        JOIN lineGraph_vertices AS r
        ON(target = r.id AND r.original_id IS NULL))
UPDATE lineGraph_vertices
  SET original_id = verticesFromEdgesWithUnassignedSource.original_id
  FROM verticesFromEdgesWithUnassignedSource
  WHERE verticesFromEdgesWithUnassignedSource.target = id;
UPDATE 8
WITH
unassignedVertices
  AS (SELECT e.id, e.original_id
        FROM lineGraph_vertices AS e
        WHERE original_id IS NOT NULL),
edgesWithUnassignedTarget
  AS (SELECT *
        FROM lineGraph_edges
        WHERE cost = 0 and target IN (SELECT id FROM unassignedVertices)),
edgesWithUnassignedTargetPlusVertices
  AS (SELECT *
        FROM edgesWithUnassignedTarget
        JOIN lineGraph_vertices
        ON(target = id)),
verticesFromEdgesWithUnassignedTarget
  AS (SELECT DISTINCT edgesWithUnassignedTargetPlusVertices.source,
                     edgesWithUnassignedTargetPlusVertices.original_id
        FROM edgesWithUnassignedTargetPlusVertices
        JOIN lineGraph_vertices AS r
        ON(source = r.id AND r.original_id IS NULL))
UPDATE lineGraph_vertices
  SET original_id = verticesFromEdgesWithUnassignedTarget.original_id
  FROM verticesFromEdgesWithUnassignedTarget
  WHERE verticesFromEdgesWithUnassignedTarget.source = id;
UPDATE 3

Los únicos vértices que quedan que no se han asignado son algunos de los vértices de hoja del grafo original. El siguiente sql completa el mapeo para estos vértices hoja (en el caso de este grafo de ejemplo no hay vértices de hoja, pero esto es necesario para grafos más grandes).

WITH
unassignedVertexIds
  AS (SELECT id
        FROM lineGraph_vertices
        WHERE original_id IS NULL),
edgesWithUnassignedSource
  AS (SELECT source,edge
        FROM lineGraph_edges
        WHERE source IN (SELECT id FROM unassignedVertexIds)),
originalEdgesWithUnassignedSource
  AS (SELECT id,source
        FROM edge_table
        WHERE id IN (SELECT edge FROM edgesWithUnassignedSource))
UPDATE lineGraph_vertices AS d
  SET original_id = (SELECT source
                       FROM originalEdgesWithUnassignedSource
                       WHERE originalEdgesWithUnassignedSource.id =
                         (SELECT edge
                            FROM edgesWithUnassignedSource
                            WHERE edgesWithUnassignedSource.source = d.id))
  WHERE id IN (SELECT id FROM unassignedVertexIds);
UPDATE 0
WITH
unassignedVertexIds
  AS (SELECT id
        FROM lineGraph_vertices
        WHERE original_id IS NULL),
edgesWithUnassignedTarget
  AS (SELECT target,edge
        FROM lineGraph_edges
        WHERE target IN (SELECT id FROM unassignedVertexIds)),
originalEdgesWithUnassignedTarget
  AS (SELECT id,target
        FROM edge_table
        WHERE id IN (SELECT edge FROM edgesWithUnassignedTarget))
UPDATE lineGraph_vertices AS d
  SET original_id = (SELECT target
                       FROM originalEdgesWithUnassignedTarget
                       WHERE originalEdgesWithUnassignedTarget.id =
                         (SELECT edge
                            FROM edgesWithUnassignedTarget
                            WHERE edgesWithUnassignedTarget.target = d.id))
  WHERE id IN (SELECT id FROM unassignedVertexIds);
UPDATE 0

Ahora nuestra tabla de mapeo de vértices está completa:

SELECT * FROM lineGraph_vertices;
 id  | original_id
-----+-------------
   2 |           2
   5 |           5
   6 |           6
   8 |           8
  10 |          10
 -11 |          10
 -10 |           6
  -9 |           8
  -5 |           5
  -4 |           5
  -3 |           5
  -2 |           5
  -1 |           2
  -8 |           5
  -7 |           5
  -6 |           5
(16 rows)

Ejemplo:	Por ejecutar la ruta más corta dijkstra con penalizaciones de giro

Un caso de uso para esta transformación de grafo es poder ejecutar una búsqueda de ruta más corta que tenga en cuenta el costo o la limitación del giro. A continuación se muestra un ejemplo de cómo ejecutar una ruta más corta dijkstra desde el vértice 2 hasta el vértice 8 en el grafo original, mientras que agrega un costo de penalización de giro de 100 al giro desde el borde 4 hasta el borde -7.

En primer lugar debemos aumentar el costo de hacer el turno a 100:

UPDATE lineGraph_edges
  SET cost = 100
  WHERE source IN (SELECT target
                     FROM lineGraph_edges
                     WHERE edge = 4) AND target IN (SELECT source
                                                      FROM lineGraph_edges
                                                      WHERE edge = -7);
UPDATE 1

A continuación, debemos ejecutar una búsqueda de ruta más corta dijkstra utilizando todos los vértices del nuevo grafo que se crearon a partir del vértice 2 como punto de partida, y todos los vértices del nuevo grafo que se crearon a partir del vértice 8 como punto final.

SELECT * FROM
  (SELECT * FROM
    (SELECT * FROM pgr_dijkstra($$SELECT seq AS id, * FROM lineGraph_edges$$,
      (SELECT array_agg(id) FROM lineGraph_vertices where original_id = 2),
      (SELECT array_agg(id) FROM lineGraph_vertices where original_id = 8)
    )) as shortestPaths
  WHERE start_vid = 2 AND end_vid = 8 AND (cost != 0 OR edge = -1)) as b;
 seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
  29 |        2 |         2 |       8 |   -1 |    1 |    1 |        0
  31 |        4 |         2 |       8 |   -4 |    5 |    1 |        1
  33 |        6 |         2 |       8 |  -10 |   25 |    1 |        2
  35 |        8 |         2 |       8 |   -3 |    4 |    1 |        3
  36 |        9 |         2 |       8 |    8 |   -1 |    0 |        4
(5 rows)

Normalmente la ruta más corta desde el vértice 2 hasta el vértice 8 tendría un costo agregado de 2, pero como hay una gran penalización por hacer el giro necesario para obtener este costo, la ruta pasa por el vértice 6 para evitar este giro.

Si hace referencia cruzada a la columna de nodo en los resultados de dijkstra con la tabla de mapeo de id de vértices, esto le mostrará que la ruta va desde v2 -> v5 -> v6 -> v5 -> v8 en el grafo original.

Ver también¶

Índices y tablas