Unsupported versions:2.6
pgr_lineGraphFull - Experimental¶
pgr_lineGraphFull — Transforms a given graph into a new graph where all of
the vertices from the original graph are converted to line graphs.
Warning
Possible server crash
These functions might create a server crash
Warning
Experimental functions
They are not officially of the current release.
They likely will not be officially be part of the next release:
The functions might not make use of ANY-INTEGER and ANY-NUMERICAL
Name might change.
Signature might change.
Functionality might change.
pgTap tests might be missing.
Might need c/c++ coding.
May lack documentation.
Documentation if any might need to be rewritten.
Documentation examples might need to be automatically generated.
Might need a lot of feedback from the comunity.
Might depend on a proposed function of pgRouting
Might depend on a deprecated function of pgRouting
Availability
Version 2.6.0
New Experimental function
Description¶
pgr_lineGraphFull, converts original directed graph to a directed line graph
by converting each vertex to a complete graph and keeping all the original
edges.
The new connecting edges have a cost 0 and go between the adjacent original
edges, respecting the directionality.
A possible application of the resulting graph is “routing with two edge restrictions”:
Setting a cost of using the vertex when routing between edges on the connecting edge
Forbid the routing between two edges by removing the connecting edge
This is possible because each of the intersections (vertices) in the original graph are now complete graphs that have a new edge for each possible turn across that intersection.
The main characteristics are:
This function is for directed graphs.
Results are undefined when a negative vertex id is used in the input graph.
Results are undefined when a duplicated edge id is used in the input graph.
Running time: TBD
Signatures¶
Summary
(seq, source, target, cost, edge)- Example:
Full line graph of subgraph of edges
SELECT * FROM pgr_lineGraphFull(
$$SELECT id, source, target, cost, reverse_cost
FROM edges
WHERE id IN (4, 7, 8, 10)$$);
seq | source | target | cost | edge
-----+--------+--------+------+------
1 | -1 | 7 | 1 | 4
2 | 6 | -1 | 0 | 0
3 | -2 | 6 | 1 | -4
4 | -3 | 3 | 1 | -7
5 | -4 | 11 | 1 | 8
6 | -5 | 8 | 1 | 10
7 | 7 | -2 | 0 | 0
8 | 7 | -3 | 0 | 0
9 | 7 | -4 | 0 | 0
10 | 7 | -5 | 0 | 0
11 | -6 | -2 | 0 | 0
12 | -6 | -3 | 0 | 0
13 | -6 | -4 | 0 | 0
14 | -6 | -5 | 0 | 0
15 | -7 | -2 | 0 | 0
16 | -7 | -3 | 0 | 0
17 | -7 | -4 | 0 | 0
18 | -7 | -5 | 0 | 0
19 | -8 | -2 | 0 | 0
20 | -8 | -3 | 0 | 0
21 | -8 | -4 | 0 | 0
22 | -8 | -5 | 0 | 0
23 | -9 | -6 | 1 | 7
24 | 3 | -9 | 0 | 0
25 | -10 | -7 | 1 | -8
26 | 11 | -10 | 0 | 0
27 | -11 | -8 | 1 | -10
28 | 8 | -11 | 0 | 0
(28 rows)
Parameters¶
Parameter |
Type |
Description |
|---|---|---|
|
Edges SQL as described below. |
Inner Queries¶
Edges SQL¶
Column |
Type |
Default |
Description |
|---|---|---|---|
|
ANY-INTEGER |
Identifier of the edge. |
|
|
ANY-INTEGER |
Identifier of the first end point vertex of the edge. |
|
|
ANY-INTEGER |
Identifier of the second end point vertex of the edge. |
|
|
ANY-NUMERICAL |
Weight of the edge ( |
|
|
ANY-NUMERICAL |
-1 |
Weight of the edge (
|
Where:
- ANY-INTEGER:
SMALLINT,INTEGER,BIGINT- ANY-NUMERICAL:
SMALLINT,INTEGER,BIGINT,REAL,FLOAT
Result Columns¶
RETURNS SET OF (seq, source, target, cost, edge)
Column |
Type |
Description |
|---|---|---|
|
|
Sequential value starting from 1.
|
|
|
Identifier of the source vertex of the current edge.
|
|
|
Identifier of the target vertex of the current edge.
|
|
|
Weight of the edge (
|
|
|
Weight of the edge (
|
Additional Examples¶
The examples of this section are based on the Sample Data network.
The examples include the subgraph including edges 4, 7, 8, and 10 with
reverse_cost.
The data¶
This example displays how this graph transformation works to create additional edges for each possible turn in a graph.
SELECT id, source, target, cost, reverse_cost
FROM edges
WHERE id IN (4, 7, 8, 10);
id | source | target | cost | reverse_cost
----+--------+--------+------+--------------
4 | 6 | 7 | 1 | 1
7 | 3 | 7 | 1 | 1
8 | 7 | 11 | 1 | 1
10 | 7 | 8 | 1 | 1
(4 rows)
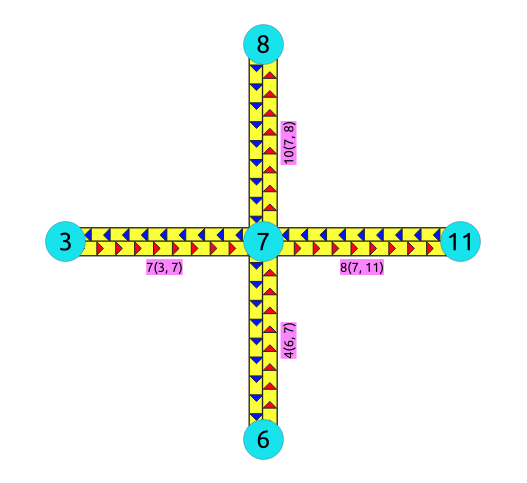
The transformation¶
SELECT * FROM pgr_lineGraphFull(
$$SELECT id, source, target, cost, reverse_cost
FROM edges
WHERE id IN (4, 7, 8, 10)$$);
seq | source | target | cost | edge
-----+--------+--------+------+------
1 | -1 | 7 | 1 | 4
2 | 6 | -1 | 0 | 0
3 | -2 | 6 | 1 | -4
4 | -3 | 3 | 1 | -7
5 | -4 | 11 | 1 | 8
6 | -5 | 8 | 1 | 10
7 | 7 | -2 | 0 | 0
8 | 7 | -3 | 0 | 0
9 | 7 | -4 | 0 | 0
10 | 7 | -5 | 0 | 0
11 | -6 | -2 | 0 | 0
12 | -6 | -3 | 0 | 0
13 | -6 | -4 | 0 | 0
14 | -6 | -5 | 0 | 0
15 | -7 | -2 | 0 | 0
16 | -7 | -3 | 0 | 0
17 | -7 | -4 | 0 | 0
18 | -7 | -5 | 0 | 0
19 | -8 | -2 | 0 | 0
20 | -8 | -3 | 0 | 0
21 | -8 | -4 | 0 | 0
22 | -8 | -5 | 0 | 0
23 | -9 | -6 | 1 | 7
24 | 3 | -9 | 0 | 0
25 | -10 | -7 | 1 | -8
26 | 11 | -10 | 0 | 0
27 | -11 | -8 | 1 | -10
28 | 8 | -11 | 0 | 0
(28 rows)
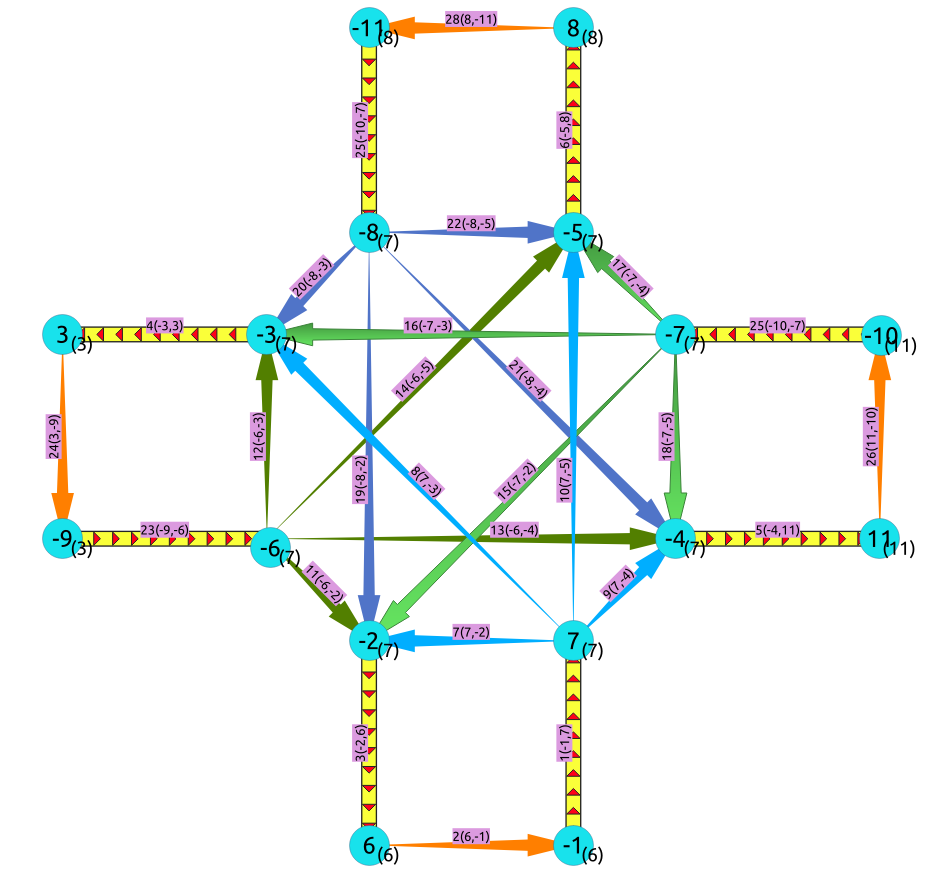
In the transformed graph, all of the edges from the original graph are still present (yellow), but we now have additional edges for every turn that could be made across vertex 7 (orange).
Creating table that identifies transformed vertices¶
The vertices in the transformed graph are each created by splitting up the vertices in the original graph. Unless a vertex in the original graph is a leaf vertex, it will generate more than one vertex in the transformed graph. One of the newly created vertices in the transformed graph will be given the same vertex identifier as the vertex that it was created from in the original graph, but the rest of the newly created vertices will have negative vertex ids.
Following is an example of how to generate a table that maps the ids of the newly created vertices with the original vertex that they were created from
Store edge results¶
The first step is to store the results of the pgr_lineGraphFull call into a
table
SELECT seq AS id, source, target, cost, edge
INTO lineGraph_edges
FROM pgr_lineGraphFull(
$$SELECT id, source, target, cost, reverse_cost
FROM edges
WHERE id IN (4, 7, 8, 10)$$);
SELECT 28
Create the mapping table¶
From the original graph’s vertex information
SELECT id, NULL::BIGINT original_id
INTO vertex_map
FROM vertices;
SELECT 17
Add the new vertices
INSERT INTO vertex_map (id)
(SELECT id
FROM pgr_extractVertices(
$$SELECT id, source, target FROM lineGraph_edges$$) WHERE id < 0);
INSERT 0 11
Filling the mapping table¶
The positive vertex identifiers are the original identifiers
UPDATE vertex_map
SET original_id = id
WHERE id > 0;
UPDATE 17
Inspecting the vertices map
SELECT *
FROM vertex_map ORDER BY id DESC;
id | original_id
-----+-------------
17 | 17
16 | 16
15 | 15
14 | 14
13 | 13
12 | 12
11 | 11
10 | 10
9 | 9
8 | 8
7 | 7
6 | 6
5 | 5
4 | 4
3 | 3
2 | 2
1 | 1
-1 |
-2 |
-3 |
-4 |
-5 |
-6 |
-7 |
-8 |
-9 |
-10 |
-11 |
(28 rows)
The self loops happen when there is no cost traveling to the target and the
source has an original value.
SELECT *, source AS targets_original_id
FROM lineGraph_edges
WHERE cost = 0 and source > 0;
id | source | target | cost | edge | targets_original_id
----+--------+--------+------+------+---------------------
2 | 6 | -1 | 0 | 0 | 6
7 | 7 | -2 | 0 | 0 | 7
8 | 7 | -3 | 0 | 0 | 7
9 | 7 | -4 | 0 | 0 | 7
10 | 7 | -5 | 0 | 0 | 7
24 | 3 | -9 | 0 | 0 | 3
26 | 11 | -10 | 0 | 0 | 11
28 | 8 | -11 | 0 | 0 | 8
(8 rows)
Updating values from self loops
WITH
self_loops AS (
SELECT DISTINCT source, target, source AS targets_original_id
FROM lineGraph_edges
WHERE cost = 0 and source > 0)
UPDATE vertex_map SET original_id = targets_original_id
FROM self_loops WHERE target = id;
UPDATE 8
Inspecting the vertices table
SELECT *
FROM vertex_map WHERE id < 0
ORDER BY id DESC;
id | original_id
-----+-------------
-1 | 6
-2 | 7
-3 | 7
-4 | 7
-5 | 7
-6 |
-7 |
-8 |
-9 | 3
-10 | 11
-11 | 8
(11 rows)
Updating from inner self loops
WITH
assigned_vertices
AS (SELECT id, original_id
FROM vertex_map
WHERE original_id IS NOT NULL),
cross_edges
AS (SELECT DISTINCT e.source, v.original_id AS source_original_id
FROM lineGraph_edges AS e
JOIN vertex_map AS v ON (e.target = v.id)
WHERE source NOT IN (SELECT id FROM assigned_vertices)
)
UPDATE vertex_map SET original_id = source_original_id
FROM cross_edges WHERE source = id;
UPDATE 3
Inspecting the vertices map
SELECT *
FROM vertex_map WHERE id < 0
ORDER BY id DESC;
id | original_id
-----+-------------
-1 | 6
-2 | 7
-3 | 7
-4 | 7
-5 | 7
-6 | 7
-7 | 7
-8 | 7
-9 | 3
-10 | 11
-11 | 8
(11 rows)
Adding a soft restriction¶
A soft restriction going from vertex 6 to vertex 3 using edges 4 -> 7 is wanted.
Idenifying the restriction¶
Running a pgr_dijkstraNear - Proposed the edge with cost 0, edge 8, is where the cost will be increased
SELECT seq, path_seq, start_vid, end_vid, node, original_id, edge, cost, agg_cost
FROM (SELECT * FROM pgr_dijkstraNear(
$$SELECT * FROM lineGraph_edges$$,
(SELECT array_agg(id) FROM vertex_map where original_id = 6),
(SELECT array_agg(id) FROM vertex_map where original_id = 3))) dn
JOIN vertex_map AS v1 ON (node = v1.id);
seq | path_seq | start_vid | end_vid | node | original_id | edge | cost | agg_cost
-----+----------+-----------+---------+------+-------------+------+------+----------
3 | 3 | -1 | 3 | -3 | 7 | 4 | 1 | 1
1 | 1 | -1 | 3 | -1 | 6 | 1 | 1 | 0
4 | 4 | -1 | 3 | 3 | 3 | -1 | 0 | 2
2 | 2 | -1 | 3 | 7 | 7 | 8 | 0 | 1
(4 rows)
The edge to be altered is WHERE cost = 0 AND seq != 1 AND edge != -1 from
the previus query:
SELECT edge FROM pgr_dijkstraNear(
$$SELECT * FROM lineGraph_edges$$,
(SELECT array_agg(id) FROM vertex_map where original_id = 6),
(SELECT array_agg(id) FROM vertex_map where original_id = 3))
WHERE cost = 0 AND seq != 1 AND edge != -1;
edge
------
8
(1 row)
Adding a value to the restriction¶
Updating the cost to the edge:
UPDATE lineGraph_edges
SET cost = 100
WHERE id IN (
SELECT edge FROM pgr_dijkstraNear(
$$SELECT * FROM lineGraph_edges$$,
(SELECT array_agg(id) FROM vertex_map where original_id = 6),
(SELECT array_agg(id) FROM vertex_map where original_id = 3))
WHERE cost = 0 AND seq != 1 AND edge != -1);
UPDATE 1
- Example:
Routing from
Now the route does not use edge 8 and does a U turn on a leaf vertex.
WITH
results AS (
SELECT * FROM pgr_dijkstraNear(
$$SELECT * FROM lineGraph_edges$$,
(SELECT array_agg(id) FROM vertex_map where original_id = 6),
(SELECT array_agg(id) FROM vertex_map where original_id = 3)))
SELECT seq, path_seq, start_vid, end_vid, node, original_id, edge, cost, agg_cost
FROM results
LEFT JOIN vertex_map AS v1 ON (node = v1.id) ORDER BY seq;
seq | path_seq | start_vid | end_vid | node | original_id | edge | cost | agg_cost
-----+----------+-----------+---------+------+-------------+------+------+----------
1 | 1 | -1 | 3 | -1 | 6 | 1 | 1 | 0
2 | 2 | -1 | 3 | 7 | 7 | 10 | 0 | 1
3 | 3 | -1 | 3 | -5 | 7 | 6 | 1 | 1
4 | 4 | -1 | 3 | 8 | 8 | 28 | 0 | 2
5 | 5 | -1 | 3 | -11 | 8 | 27 | 1 | 2
6 | 6 | -1 | 3 | -8 | 7 | 20 | 0 | 3
7 | 7 | -1 | 3 | -3 | 7 | 4 | 1 | 3
8 | 8 | -1 | 3 | 3 | 3 | -1 | 0 | 4
(8 rows)
Simplifying leaf vertices¶
In this example, there is no additional cost for traversing a leaf vertex.
Using the vertex map give the leaf verices their original value.¶
On the source column
WITH
u_turns AS (
SELECT e.id AS eid, v1.original_id
FROM linegraph_edges as e
JOIN vertex_map AS v1 ON (source = v1.id)
AND v1.original_id IN (3, 6, 8, 11))
UPDATE lineGraph_edges
SET source = original_id
FROM u_turns
WHERE id = eid;
UPDATE 8
On the target column
WITH
u_turns AS (
SELECT e.id AS eid, v1.original_id
FROM linegraph_edges as e
JOIN vertex_map AS v1 ON (target = v1.id)
AND v1.original_id IN (3, 6, 8, 11))
UPDATE lineGraph_edges
SET target = original_id
FROM u_turns
WHERE id = eid;
UPDATE 8
Removing self loops on leaf nodes¶
The self loops of the leaf nodes are
SELECT * FROM linegraph_edges
WHERE source = target
ORDER BY id;
id | source | target | cost | edge
----+--------+--------+------+------
2 | 6 | 6 | 0 | 0
24 | 3 | 3 | 0 | 0
26 | 11 | 11 | 0 | 0
28 | 8 | 8 | 0 | 0
(4 rows)
Which can be removed
DELETE FROM linegraph_edges
WHERE source = target;
DELETE 4
- Example:
Routing from
Routing can be done now using the original vertices id using pgr_dijkstra
WITH
results AS (
SELECT * FROM pgr_dijkstra(
$$SELECT * FROM lineGraph_edges$$, 6, 3))
SELECT seq, path_seq, node, original_id, edge, cost, agg_cost
FROM results
LEFT JOIN vertex_map AS v1 ON (node = v1.id) ORDER BY seq;
seq | path_seq | node | original_id | edge | cost | agg_cost
-----+----------+------+-------------+------+------+----------
1 | 1 | 6 | 6 | 1 | 1 | 0
2 | 2 | 7 | 7 | 9 | 0 | 1
3 | 3 | -4 | 7 | 5 | 1 | 1
4 | 4 | 11 | 11 | 25 | 1 | 2
5 | 5 | -7 | 7 | 16 | 0 | 3
6 | 6 | -3 | 7 | 4 | 1 | 3
7 | 7 | 3 | 3 | -1 | 0 | 4
(7 rows)
Complete routing graph¶
Add edges from the original graph¶
Add all the edges that are not involved in the line graph process to the new table
SELECT id, source, target, cost, reverse_cost
INTO new_graph from edges
WHERE id NOT IN (4, 7, 8, 10);
SELECT 14
Some administrative tasks to get new identifiers for the edges
CREATE SEQUENCE new_graph_id_seq;
CREATE SEQUENCE
ALTER TABLE new_graph ALTER COLUMN id SET DEFAULT nextval('new_graph_id_seq');
ALTER TABLE
ALTER TABLE new_graph ALTER COLUMN id SET NOT NULL;
ALTER TABLE
ALTER SEQUENCE new_graph_id_seq OWNED BY new_graph.id;
ALTER SEQUENCE
SELECT setval('new_graph_id_seq', (SELECT max(id) FROM new_graph));
setval
--------
18
(1 row)
Add the newly calculated edges¶
INSERT INTO new_graph (source, target, cost, reverse_cost)
SELECT source, target, cost, -1 FROM lineGraph_edges;
INSERT 0 24
Using the routing graph¶
When using this method for routing with soft restrictions there will be uturns
- Example:
Routing from
WITH
results AS (
SELECT * FROM pgr_dijkstra(
$$SELECT * FROM new_graph$$, 6, 3))
SELECT seq, path_seq, node, original_id, edge, cost, agg_cost
FROM results
LEFT JOIN vertex_map AS v1 ON (node = v1.id) ORDER BY seq;
seq | path_seq | node | original_id | edge | cost | agg_cost
-----+----------+------+-------------+------+------+----------
1 | 1 | 6 | 6 | 35 | 1 | 0
2 | 2 | 7 | 7 | 20 | 0 | 1
3 | 3 | -4 | 7 | 41 | 1 | 1
4 | 4 | 11 | 11 | 37 | 1 | 2
5 | 5 | -7 | 7 | 27 | 0 | 3
6 | 6 | -3 | 7 | 40 | 1 | 3
7 | 7 | 3 | 3 | -1 | 0 | 4
(7 rows)
- Example:
Routing from
WITH
results AS (
SELECT * FROM pgr_dijkstra(
$$SELECT * FROM new_graph$$, 5, 1))
SELECT seq, path_seq, node, original_id, edge, cost, agg_cost
FROM results
LEFT JOIN vertex_map AS v1 ON (node = v1.id) ORDER BY seq;
seq | path_seq | node | original_id | edge | cost | agg_cost
-----+----------+------+-------------+------+------+----------
1 | 1 | 5 | 5 | 1 | 1 | 0
2 | 2 | 6 | 6 | 35 | 1 | 1
3 | 3 | 7 | 7 | 20 | 0 | 2
4 | 4 | -4 | 7 | 41 | 1 | 2
5 | 5 | 11 | 11 | 37 | 1 | 3
6 | 6 | -7 | 7 | 27 | 0 | 4
7 | 7 | -3 | 7 | 40 | 1 | 4
8 | 8 | 3 | 3 | 6 | 1 | 5
9 | 9 | 1 | 1 | -1 | 0 | 6
(9 rows)
See Also¶
Indices and tables
