pgr_isPlanar - 实验

pgr_isPlanar — 根据图的平面性返回布尔值.

Boost 图内部

Warning

可能服务器崩溃

• 这些功能可能会导致服务器崩溃

Warning

实验功能

• 它们不是当前版本的正式版本。

• 它们可能不会正式成为下一个版本的一部分：

  • 这些函数可能不使用 ANY-INTEGER 和 ANY-NUMERICAL

  • 名称可能会改变。

  • 签名可能会改变。

  • 功能可能会改变。

  • pgTap 测试可能丢失。

  • 可能需要 c/c++编码。

  • 可能缺乏文档。

  • 文档（如果有）可能需要重写。

  • 可能需要自动生成文档示例。

  • 可能需要社区的大量反馈。

  • 可能取决于 pgRouting 的拟议功能

  • 可能依赖于 pgRouting 的已弃用函数

可用性

• 版本3.2.0

  • 新 实验 函数

描述

如果一个图可以在二维空间中绘制，使得它的任意两条边都不相交，那么这个图就是平面图。这种平面图的绘制称为平面绘图。每个平面图也可以表示为一个直线绘图，即在平面绘图中，每条边都由一条线段表示。当一个图包含 \(K_5\) 或 \(K_{3, 3}\) 作为子图时，这个图就不是平面图。

主要特点是：

• 此实施使用 Boyer-Myrvold 平面度测试。

• 它将根据图形的平面性返回一个布尔值。

• 仅适用于 无向 图。

• 该算法在计算中不考虑遍历成本。

• 运行时间： \(O(|V|)\)

签名

总结

pgr_isPlanar(Edges SQL)

RETURNS BOOLEAN

SELECT * FROM pgr_isPlanar(
  'SELECT id, source, target, cost, reverse_cost
  FROM edges'
);
 pgr_isplanar
--------------
 t
(1 row)

参数

参数	类型	描述
Edges SQL	TEXT	Edges SQL 如下所述。

内部查询

Edges SQL

列	类型	默认	描述
id	ANY-INTEGER		边的标识符。
source	ANY-INTEGER		边的第一个端点顶点的标识符。
target	ANY-INTEGER		边的第二个端点顶点的标识符。
cost	ANY-NUMERICAL		边(source, target)的权重
reverse_cost	ANY-NUMERICAL	-1	边(target, source)的权重 当为负时：边（ target, source ）不存在，因此它不是图的一部分。

其中：

ANY-INTEGER:

SMALLINT, INTEGER, BIGINT

ANY-NUMERICAL:

SMALLINT, INTEGER, BIGINT, REAL, FLOAT

结果列

返回一个布尔值 (pgr_isplanar)

列	类型	描述
pgr_isplanar	BOOLEAN	当图形是平面时为 true。 当图形不是平面时为 false。

其他示例

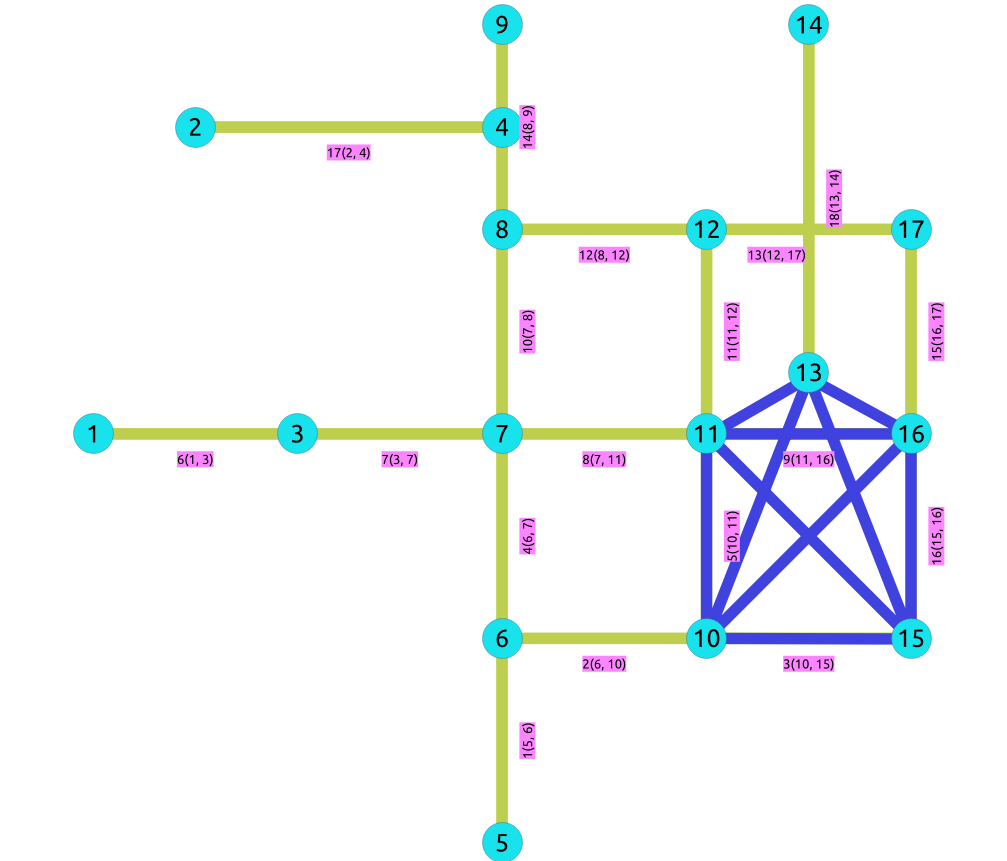
以下边将构成具有顶点 {10, 15, 11, 16, 13} 的子图，这个子图是一个 \(K_1\) 图。

INSERT INTO edges (source, target, cost, reverse_cost) VALUES
  (10, 16, 1, 1), (10, 13, 1, 1),
  (15, 11, 1, 1), (15, 13, 1, 1),
  (11, 13, 1, 1), (16, 13, 1, 1);
INSERT 0 6

新图不是平面图，因为它具有一个 \(K_5\) 子图。蓝色的边代表 \(K_5\) 子图。

SELECT * FROM pgr_isPlanar(
  'SELECT id, source, target, cost, reverse_cost
  FROM edges');
 pgr_isplanar
--------------
 f
(1 row)

另请参阅

• 示例数据

• https://www.boost.org/libs/graph/doc/boyer_myrvold.html

索引和表格

• Index

• Search Page