Unsupported versions:2.6 2.5 2.4 2.3
pgr_TSPeuclidean¶
pgr_TSPeuclidean- 使用 metric 算法进行近似计算。
可用性:
Version 4.0.0
Simulated Annealing signature removed
Results change depending on input order
版本3.2.1
Simulated Annealing算法不再受支持
Simulated Annealing 算法相关参数被忽略: max_processing_time, tries_per_temperature, max_changes_per_temperature, max_consecutive_non_changes, initial_temperature, final_temperature, cooling_factor, randomize
版本3.0.0
pgr_eucledianTSP 的名称更改
版本2.3.0
新官方函数说明。
描述¶
问题定义¶
旅行推销员问题 (TSP) 提出以下问题:
给定一个城市列表以及每对城市之间的距离,哪条是访问每个城市一次并返回出发城市的最短路线?
特征¶
该问题是一个NP-hard优化问题。
使用度量算法
Implementation generates solutions that are twice as long as the optimal tour in the worst case:
Graph characteristics for best performance:
图是无向的
图是全连通的
图中,边上的旅行成本服从三角不等式。
旅行费用是对称的:
从
u到v的旅行费用与从v到u的旅行费用相同
Results change depending on input order of the Coordinates SQL
任何重复的标识符都会被忽略,保留的坐标是任意选择的。
对于相同的标识符,坐标非常相似,例如
1, 3.5, 1 1, 3.499999999999 0.9999999
对于相同的标识符,坐标有很大不同,例如:
2, 3.5, 1.0 2, 3.6, 1.1
签名¶
总结
[start_id, end_id])(seq, node, cost, agg_cost) 的集合- 示例:
有默认值
SELECT * FROM pgr_TSPeuclidean(
$$
SELECT id, st_X(geom) AS x, st_Y(geom)AS y FROM vertices ORDER BY id
$$);
seq | node | cost | agg_cost
-----+------+----------------+---------------
1 | 1 | 0 | 0
2 | 6 | 2.2360679775 | 2.2360679775
3 | 5 | 1 | 3.2360679775
4 | 10 | 1.41421356237 | 4.65028153987
5 | 7 | 1.41421356237 | 6.06449510225
6 | 2 | 2.12132034356 | 8.18581544581
7 | 9 | 1.58113883008 | 9.76695427589
8 | 4 | 0.5 | 10.2669542759
9 | 14 | 1.58113883009 | 11.848093106
10 | 17 | 1.11803398875 | 12.9661270947
11 | 16 | 1 | 13.9661270947
12 | 15 | 1 | 14.9661270947
13 | 11 | 1.41421356237 | 16.3803406571
14 | 13 | 0.583095189485 | 16.9634358466
15 | 12 | 0.860232526704 | 17.8236683733
16 | 8 | 1 | 18.8236683733
17 | 3 | 1.41421356237 | 20.2378819357
18 | 1 | 1 | 21.2378819357
(18 rows)
参数¶
参数 |
类型 |
描述 |
|---|---|---|
|
Coordinates SQL 如下所述 |
TSP 可选参数¶
列 |
类型 |
默认 |
描述 |
|---|---|---|---|
|
ANY-INTEGER |
|
第一个访问顶点
|
|
ANY-INTEGER |
|
返回
|
内部查询¶
坐标SQL¶
列 |
类型 |
描述 |
|---|---|---|
|
|
起始顶点的标识符。 |
|
|
坐标的X值。 |
|
|
坐标的Y值。 |
结果列¶
返回集合 (seq, node, cost, agg_cost)
列 |
类型 |
描述 |
|---|---|---|
seq |
|
行顺序。 |
node |
|
节点/坐标/点的标识符。 |
cost |
|
从路径序列中的当前
|
agg_cost |
|
从
|
其他示例¶
测试西撒哈拉29个城市¶
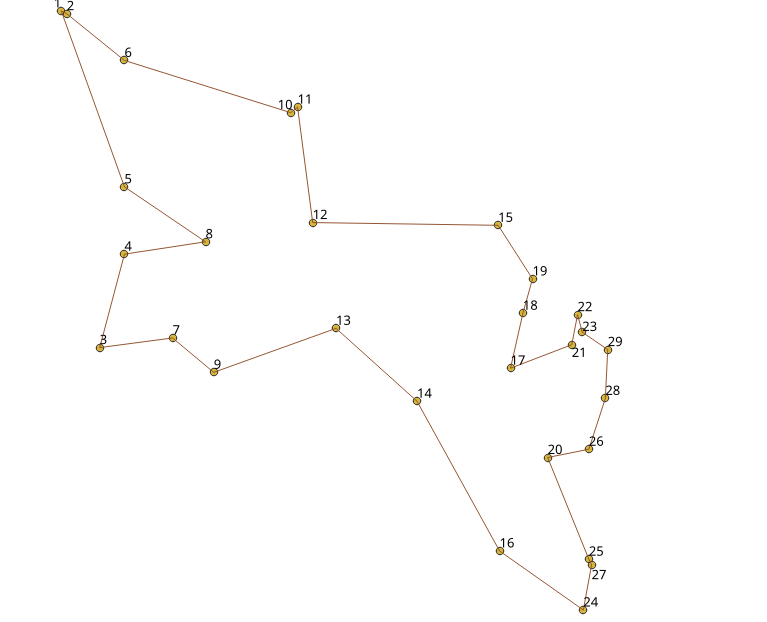
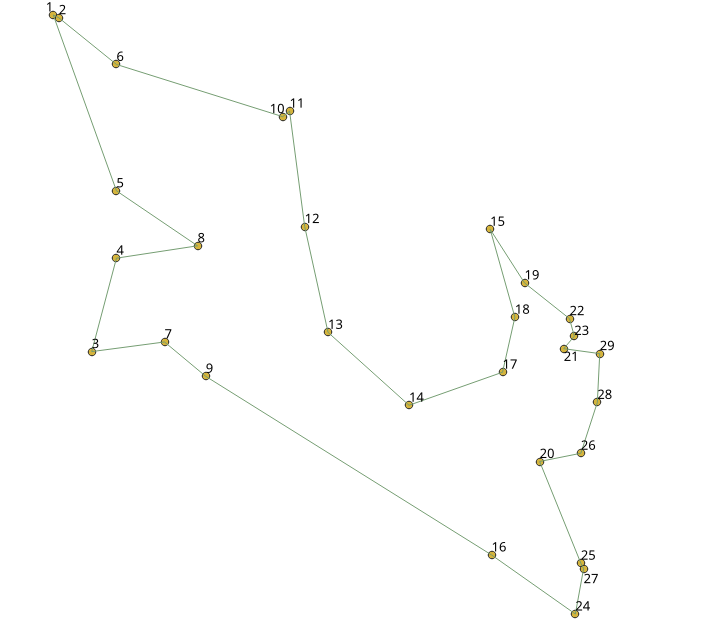
此示例展示了如何使用Waterloo大学的 示例数据 ,使用29 个城市的数据集 Western Sahara dataset 进行性能测试
创建数据表并存储数据¶
CREATE TABLE wi29 (id BIGINT, x FLOAT, y FLOAT, geom geometry);
INSERT INTO wi29 (id, x, y) VALUES
(1,20833.3333,17100.0000),
(2,20900.0000,17066.6667),
(3,21300.0000,13016.6667),
(4,21600.0000,14150.0000),
(5,21600.0000,14966.6667),
(6,21600.0000,16500.0000),
(7,22183.3333,13133.3333),
(8,22583.3333,14300.0000),
(9,22683.3333,12716.6667),
(10,23616.6667,15866.6667),
(11,23700.0000,15933.3333),
(12,23883.3333,14533.3333),
(13,24166.6667,13250.0000),
(14,25149.1667,12365.8333),
(15,26133.3333,14500.0000),
(16,26150.0000,10550.0000),
(17,26283.3333,12766.6667),
(18,26433.3333,13433.3333),
(19,26550.0000,13850.0000),
(20,26733.3333,11683.3333),
(21,27026.1111,13051.9444),
(22,27096.1111,13415.8333),
(23,27153.6111,13203.3333),
(24,27166.6667,9833.3333),
(25,27233.3333,10450.0000),
(26,27233.3333,11783.3333),
(27,27266.6667,10383.3333),
(28,27433.3333,12400.0000),
(29,27462.5000,12992.2222);
添加几何图形(用于视觉目的)¶
UPDATE wi29 SET geom = ST_makePoint(x,y);
旅游总费用¶
获取旅行的总成本,将该值与数据集上给出的最佳旅行长度 27603 进行比较
SELECT *
FROM pgr_TSPeuclidean($$SELECT * FROM wi29 ORDER BY id$$)
WHERE seq = 30;
seq | node | cost | agg_cost
-----+------+---------------+---------------
30 | 1 | 2266.91173136 | 28777.4854127
(1 row)
获取游览的几何形状¶
WITH
tsp_results AS (SELECT seq, geom FROM pgr_TSPeuclidean($$SELECT * FROM wi29$$) JOIN wi29 ON (node = id))
SELECT ST_MakeLine(ARRAY(SELECT geom FROM tsp_results ORDER BY seq));
st_makeline
--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
01020000001E000000F085C9545558D4400000000000B3D040000000000069D440107A36ABAAAAD040000000000018D54000000000001DD040107A36AB2A10D7401FF46C5655FDCE40000000000025D740E10B93A9AA1ECF40F085C954D552D740E10B93A9AA62CC40107A36ABAA99D7400000000000E1C940107A36AB4A8FD840E10B93A9EA26C840F085C954D5AAD9401FF46C5655EFC840F085C95455D0D940E10B93A9AA3CCA40F085C9545585D940000000000052CC400000000080EDD94000000000000DCB40A52C431C0776DA40E10B93A9EA33CA40A52C431C6784DA40E10B93A9AAC9C940A52C431C8764DA402C6519E2F87DC94000000000A0D1DA4096B20C711C60C940F085C95455CADA40000000000038C840F085C9545598DA40E10B93A9AA03C740F085C954551BDA40E10B93A9AAD1C640F085C9545598DA40000000000069C440107A36ABAAA0DA40E10B93A9AA47C440107A36ABAA87DA40E10B93A9AA34C340000000008089D94000000000009BC440F085C954D526D6401FF46C5655D6C840F085C954D5A9D540E10B93A9AAA6C9400000000000CDD4401FF46C56556CC940000000000018D5400000000000A3CB40F085C954D50DD6400000000000EECB40000000000018D5401FF46C56553BCD40F085C9545558D4400000000000B3D040
(1 row)
视觉效果¶
从视觉上比较,第一个图展示了 最优解 ,而第二个图展示了使用 pgr_TSPeuclidean 所得到的解。
另请参阅¶
索引和表格
