Supported versions: latest (3.8) 3.7 3.6 3.5 3.4 main dev

pgr_degree

pgr_degree —对于无向图中的每个顶点，返回与该顶点关联的边的计数。

Proposed

Warning

下一版本的提议功能。

• 它们并未正式出现在当前版本中。

• 它们可能会正式成为下一个版本的一部分：

  • 这些函数使用 ANY-INTEGER 和 ANY-NUMERICAL

  • 名字可能不会改变。（但仍然有可能改变）

  • 签名可能不会改变。（但仍然有可能改变）

  • 功能可能不会改变。（但仍然有可能改变）

  • pgTap 测试已经完成。 但可能需要更多。

  • 文档可能需要完善。

可用性

Version 3.8.0

• 错误信息调整。

• 只有 Edges SQL 的新签名。

• 函数正式发布。

版本 3.4.0

• 新提议的函数。

描述

计算无向图顶点的度数

图中顶点的度（或称为顶点的连接度）是指与该顶点相关联的边数。

• 适用于 无向 图。

• 一个循环对一个顶点的度数贡献为 2。

• 度数为 0 的顶点称为孤立顶点。

  • 孤立顶点不包含在结果中

• 未参与子图的顶点被视为孤立顶点。

• 可以执行 dryrun ，用于获取答案的代码将显示在 PostgreSQL 的 NOTICE 。

  • 该代码可用作满足特定应用要求的基础代码。

• 不执行排序操作。

签名

pgr_degree(Edges SQL , [dryrun])

pgr_degree(Edges SQL , Vertex SQL, [dryrun])

RETURNS SETOF (node, degree)

OR EMPTY SET

边

pgr_degree(Edges SQL , [dryrun])

RETURNS SETOF (node, degree)

OR EMPTY SET

示例:

获取边线表定义的顶点度数

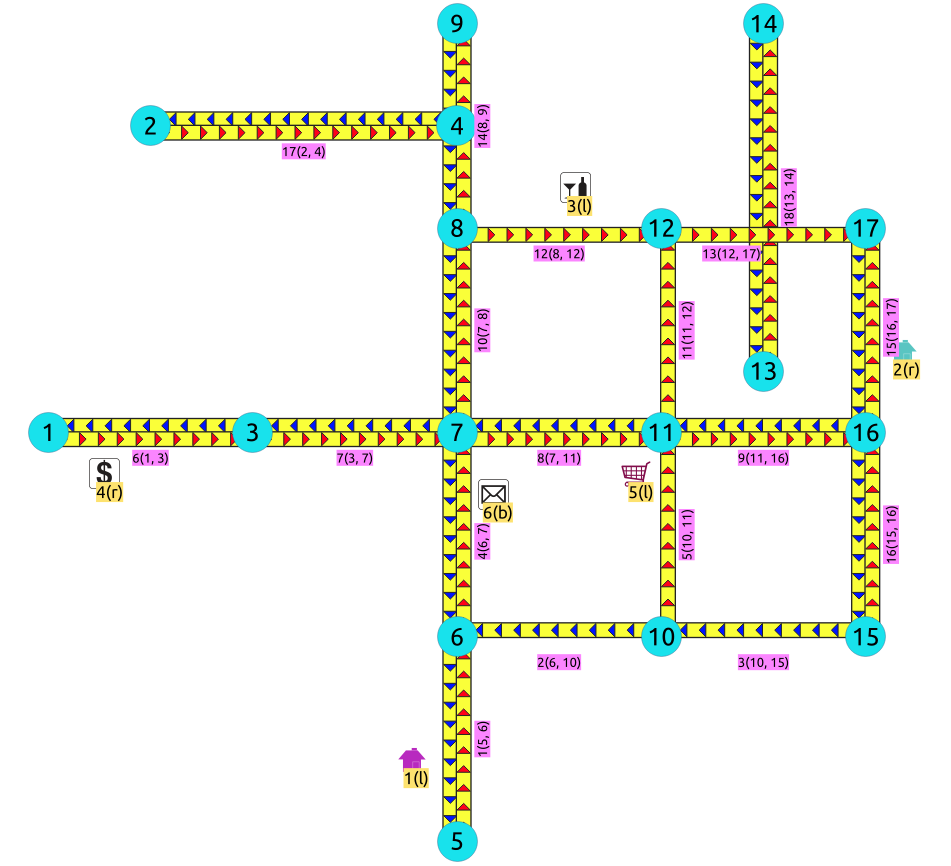
SELECT * FROM pgr_degree($$SELECT id, source, target FROM edges$$)
ORDER BY node;
 node | degree
------+--------
    1 |      1
    2 |      1
    3 |      2
    4 |      1
    5 |      1
    6 |      3
    7 |      4
    8 |      3
    9 |      1
   10 |      3
   11 |      4
   12 |      3
   13 |      1
   14 |      1
   15 |      2
   16 |      3
   17 |      2
(17 rows)

边和顶点

pgr_degree(Edges SQL , Vertex SQL, [dryrun])

RETURNS SETOF (node, degree)

OR EMPTY SET

示例:

提取顶点信息

pgr_degree 可以使用 pgr_extractVertices 嵌入调用。

对于适当规模的网络，最好事先准备好顶点表，并在调用 pgr_degree 时使用。 (请参阅 Using a vertex table)

计算节点的度数：

SELECT * FROM pgr_degree(
  $$SELECT id FROM edges$$,
  $$SELECT id, in_edges, out_edges
    FROM pgr_extractVertices('SELECT id, geom FROM edges')$$);
 node | degree
------+--------
    1 |      1
    2 |      1
    3 |      2
    4 |      1
    5 |      1
    6 |      3
    7 |      4
    8 |      3
    9 |      1
   10 |      3
   11 |      4
   12 |      3
   13 |      1
   14 |      1
   15 |      2
   16 |      3
   17 |      2
(17 rows)

参数

参数	类型	描述
Edges SQL	TEXT	Edges SQL 如下所述
Vertex SQL	TEXT	Vertex SQL 如下所述

可选参数

参数	类型	默认	描述
dryrun	BOOLEAN	false	当为真时，不要处理查询，而是获取一个通知（NOTICE）来显示查询的结果。

内部查询

Edges SQL

关于 Edges and Vertices 签名：

列	类型	描述
id	BIGINT	边的标识符。

关于 Edges 签名：

列	类型	描述
id	BIGINT	边的标识符。
source	BIGINT	边的第一个端点顶点的标识符。
target	BIGINT	边的第二个端点顶点的标识符。

Vertex SQL

关于 Edges and Vertices 签名：

列	类型	描述
id	BIGINT	边的第一个端点顶点的标识符。
in_edges	BIGINT[]	以顶点 id 作为 第一个端点 的边的标识符数组。 当缺失时， out_edges 必须存在。
out_edges	BIGINT[]	以顶点 id 作为 第二个端点 的边的标识符数组。 缺失时， in_edges 必须存在。

结果列

列	类型	描述
node	BIGINT	顶点标识符
degree	BIGINT	与顶点 id 关联的边数

其他示例

循环度

一个循环对一个顶点的度数贡献为 2。

使用 Edges 签名。

SELECT * from pgr_degree('SELECT 1 as id, 2 as source, 2 as target');
 node | degree
------+--------
    2 |      2
(1 row)

使用 Edges and Vertices 签名。

SELECT * FROM pgr_degree(
  $$SELECT 1 AS id$$,
  $$SELECT id, in_edges, out_edges
     FROM pgr_extractVertices('SELECT 1 as id, 2 as source, 2 as target')$$);
 node | degree
------+--------
    2 |      2
(1 row)

子图的度数

下面是 示例数据 的子图：

• $E=\{(1,5\leftrightarrow 6),(1,6\leftrightarrow 10)\}$

• $V=\{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17\}$

未参与边的顶点被视为孤立顶点

• 在子图中的阶数为 0，并且

• 它们的度数不会在输出结果中显示。

使用 Edges 签名。

SELECT * FROM pgr_degree($$SELECT * FROM edges WHERE id IN (1, 2)$$);
 node | degree
------+--------
   10 |      1
    6 |      2
    5 |      1
(3 rows)

使用 Edges and Vertices 签名。

SELECT * FROM pgr_degree(
  $$SELECT * FROM edges WHERE id IN (1, 2)$$,
  $$SELECT id, in_edges, out_edges FROM vertices$$);
 node | degree
------+--------
    5 |      1
    6 |      2
   10 |      1
(3 rows)

使用顶点表

对于较大规模的网络，建议预先准备顶点表并在调用 pgr_degree 时使用。

提取顶点信息并保存到表格中：

CREATE TABLE vertices AS
SELECT id, in_edges, out_edges
FROM pgr_extractVertices('SELECT id, geom FROM edges');
SELECT 17

计算节点的度数：

SELECT * FROM pgr_degree(
  $$SELECT id FROM edges$$,
  $$SELECT id, in_edges, out_edges FROM vertices$$);
 node | degree
------+--------
    1 |      1
    2 |      1
    3 |      2
    4 |      1
    5 |      1
    6 |      3
    7 |      4
    8 |      3
    9 |      1
   10 |      3
   11 |      4
   12 |      3
   13 |      1
   14 |      1
   15 |      2
   16 |      3
   17 |      2
(17 rows)

模拟执行

要获取用于生成顶点信息的查询，请使用 dryrun => true 。

结果可作为基础代码，根据后台开发需要进行改进。

SELECT * FROM pgr_degree(
  $$SELECT id FROM edges WHERE id < 17$$,
  $$SELECT id, in_edges, out_edges FROM vertices$$,
  dryrun => true);
NOTICE:
    WITH

    -- a sub set of edges of the graph goes here
    g_edges AS (
      SELECT id FROM edges WHERE id < 17
    ),

    -- sub set of vertices of the graph goes here
    all_vertices AS (
      SELECT id, in_edges, out_edges FROM vertices
    ),

    g_vertices AS (
      SELECT id,
        unnest(
          coalesce(in_edges::BIGINT[], '{}'::BIGINT[])
          ||
          coalesce(out_edges::BIGINT[], '{}'::BIGINT[])) AS eid
      FROM all_vertices
    ),

    totals AS (
      SELECT v.id, count(*)
      FROM g_vertices v
      JOIN g_edges e ON (v.eid = e.id) GROUP BY v.id
    )

    SELECT id::BIGINT, count::BIGINT FROM all_vertices JOIN totals USING (id)
    ;
 node | degree
------+--------
(0 rows)

查找断头节点

如果已经使用 pgr_extractVertices 构建了顶点表，并且想要获取整个图的度数，而不是子集的度数，则可以跳过使用 pgr_degree ，直接操作 in_edges 和 out_edges 列。

断头节点的度数为 1。

获取死端：

SELECT id FROM vertices
WHERE array_length(in_edges || out_edges, 1) = 1;
 id
----
  1
  2
  5
(3 rows)

死端（Dead End）的形成条件

• 死端顶点（Dead End Vertex）的拓扑定义。

• 该顶点位于导入图形的边界处。

  • 如果导入了更大的图，则该顶点可能不会是死端

节点 $4$ 在查询中是一个死端，即使从视觉上看它是三条边的终点。

节点 $4$ 是死端还是非死端？

这个问题的答案将取决于应用情况。

• 有这么小的路边吗：

  • 这不允许车辆使用该视觉交叉路口？

  • 是否适用于行人，因此行人可以轻松地在小路边行走？

  • 电力和电线的应用是否可以轻松地延伸到小路边顶部？

• 是否有一个大悬崖，从鹰的角度看，死胡同靠近该路段？

根据分析结果，可能需要对数据进行修改。

当存在大量断头节点时，可调用 收缩 - 函数族 函数族收缩图形结构以加速处理。

查找线性顶点

线性顶点的阶数为 2。

若已使用 pgr_extractVertices 构建顶点表

要获得线性边：

SELECT id FROM vertices
WHERE array_length(in_edges || out_edges, 1) = 2;
 id
----
  3
  9
 13
 15
 16
(5 rows)

当这些顶点表示减速带、停止信号，并且应用程序将其纳入考虑时，这些线性顶点是正确的。

当图中存在许多不需要考虑的线性顶点时，为了加速处理，可以使用 收缩 - 函数族 函数来简化问题。

另请参阅

• 实用工具函数集

• pgr_extractVertices

索引和表格

• Index

• Search Page