Versiones soportadas: latest (3.8) 3.7 3.6 3.5 3.4 main dev

pgr_degree

pgr_degree - Para cada vértice de un grafo no dirigido, devuelve el número de aristas incidentes en el vértice.

Proposed

Advertencia

Funciones propuestas para la próxima versión mayor.

• No están oficialmente en la versión actual.

• Es probable que oficialmente formen parte del próximo lanzamiento:

  • Las funciones hacen uso de ENTEROS y FLOTANTES

  • Probablemente el nombre no cambie. (Pero todavía puede)

  • Es posible que la firma no cambie. (Pero todavía puede)

  • Probablemente la funcionalidad no cambie. (Pero todavía puede)

  • Se han hecho pruebas con pgTap. Pero tal vez se necesiten más.

  • Es posible que la documentación necesite un refinamiento.

Disponibilidad

Versión 3.8.0

• Error messages adjustment.

• New signature with only Edges SQL.

• Función promovida a oficial.

Versión 3.4.0

• Nueva función propuesta.

Descripción

Calcula el grado de los vértices de un grafo no dirigido

El grado (o valencia) de un vértice de un grafo es el número de aristas incidentes al vértice.

• Funciona para grafos no dirigidos.

• A loop contributes 2 to a vertex’s degree.

• A vertex with degree 0 is called an isolated vertex.

  • Vértice aislado no forma parte del resultado

• Vertex not participating on the subgraph is considered and isolated vertex.

• Dado que se trata de una ejecución dryrun, el código de todos los cálculos se muestra en el NOTICE de PostgreSQL.

  • The code can be used as base code for the particular application requirements.

• No se realiza ningún ordenamiento.

Firmas

pgr_degree(Edges SQL , [dryrun])

pgr_degree(SQL de aristas , SQL de vértices, [dryrun])

REGRESA CONJUNTO DE (node, degree)

O CONJUNTO VACÍO

Edges

pgr_degree(Edges SQL , [dryrun])

REGRESA CONJUNTO DE (node, degree)

O CONJUNTO VACÍO

ejemplo:

Obtener el grado de los vértices definidos en la tabla de aristas

SELECT * FROM pgr_degree($$SELECT id, source, target FROM edges$$)
ORDER BY node;
 node | degree
------+--------
    1 |      1
    2 |      1
    3 |      2
    4 |      1
    5 |      1
    6 |      3
    7 |      4
    8 |      3
    9 |      1
   10 |      3
   11 |      4
   12 |      3
   13 |      1
   14 |      1
   15 |      2
   16 |      3
   17 |      2
(17 rows)

Aristas y Vértices

pgr_degree(SQL de aristas , SQL de vértices, [dryrun])

REGRESA CONJUNTO DE (node, degree)

O CONJUNTO VACÍO

Ejemplo:

Extraer la información del vértice

pgr_degree can use pgr_extractVertices embedded in the call.

For decent size networks, it is best to prepare your vertices table before hand and use it on pgr_degree calls. (See Using a vertex table)

Calcula el grado de los vértices:

SELECT * FROM pgr_degree(
  $$SELECT id FROM edges$$,
  $$SELECT id, in_edges, out_edges
    FROM pgr_extractVertices('SELECT id, geom FROM edges')$$);
 node | degree
------+--------
    1 |      1
    2 |      1
    3 |      2
    4 |      1
    5 |      1
    6 |      3
    7 |      4
    8 |      3
    9 |      1
   10 |      3
   11 |      4
   12 |      3
   13 |      1
   14 |      1
   15 |      2
   16 |      3
   17 |      2
(17 rows)

Parámetros

Parámetro	Tipo	Descripción
SQL de aristas	TEXT	SQL de aristas como se describe a continuación
SQL de vértices	TEXT	Vertex SQL como se describe abajo

Parámetros opcionales

Parámetro	Tipo	x Defecto	Descripción
dryrun	BOOLEAN	false	Cuando verdadero, no procesar y recibir un AVISO de la consulta resultante.

Consultas Internas

SQL aristas

Para la firma Aristas y Vértices:

Columna	Tipo	Descripción
id	BIGINT	Identificador de la arista.

Para la firma Aristas:

Columna	Tipo	Descripción
id	BIGINT	Identificador de la arista.
source	BIGINT	Identificador del primer vértice de la arista.
target	BIGINT	Identificador del segundo vértice de la arista.

SQL de vértices

Para la firma Aristas y Vértices:

Columna	Tipo	Descripción
id	BIGINT	Identificador del primer vértice de la arista.
in_edges	BIGINT[]	Arreglo de identificadores de las aristas que tienen el vértice id como primer punto final. Si falta, out_edges debe existir.
out_edges	BIGINT[]	Arreglo de identificadores de las aristas que tienen el vértice id como segundo punto final. Si falta, in_edges debe existir.

Columnas de resultados

Columna	Tipo	Descripción
node	BIGINT	Identificador de vértice
degree	BIGINT	Número de aristas incidentes al vértice id

Ejemplos Adicionales

Grado de un bucle

A loop contributes 2 to a vertex’s degree.

Usando la firma Aristas.

SELECT * from pgr_degree('SELECT 1 as id, 2 as source, 2 as target');
 node | degree
------+--------
    2 |      2
(1 row)

Using the Edges and Vertices signature.

SELECT * FROM pgr_degree(
  $$SELECT 1 AS id$$,
  $$SELECT id, in_edges, out_edges
     FROM pgr_extractVertices('SELECT 1 as id, 2 as source, 2 as target')$$);
 node | degree
------+--------
    2 |      2
(1 row)

Grado de un subgrafo

Para el siguiente sub-grafo de Datos Muestra:

• $E=\{(1,5\leftrightarrow 6),(1,6\leftrightarrow 10)\}$

• $V=\{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17\}$

The vertices not participating on the edge are considered isolated

• their degree is 0 in the subgraph and

• their degree is not shown in the output.

Usando la firma Aristas.

SELECT * FROM pgr_degree($$SELECT * FROM edges WHERE id IN (1, 2)$$);
 node | degree
------+--------
   10 |      1
    6 |      2
    5 |      1
(3 rows)

Using the Edges and Vertices signature.

SELECT * FROM pgr_degree(
  $$SELECT * FROM edges WHERE id IN (1, 2)$$,
  $$SELECT id, in_edges, out_edges FROM vertices$$);
 node | degree
------+--------
    5 |      1
    6 |      2
   10 |      1
(3 rows)

Usando una tabla de vértices

Para un tamaño de red razonable, es mejor preparar previamente una tabla de vértices y utilizarla en las llamadas a pgr_degree.

Extraer la información del vértice y almacenar en una tabla:

CREATE TABLE vertices AS
SELECT id, in_edges, out_edges
FROM pgr_extractVertices('SELECT id, geom FROM edges');
SELECT 17

Calcula el grado de los vértices:

SELECT * FROM pgr_degree(
  $$SELECT id FROM edges$$,
  $$SELECT id, in_edges, out_edges FROM vertices$$);
 node | degree
------+--------
    1 |      1
    2 |      1
    3 |      2
    4 |      1
    5 |      1
    6 |      3
    7 |      4
    8 |      3
    9 |      1
   10 |      3
   11 |      4
   12 |      3
   13 |      1
   14 |      1
   15 |      2
   16 |      3
   17 |      2
(17 rows)

Ejecución de prueba

Para obtener la consulta generada que se usa para obtener la información de vértices, utilizar dryrun := true.

Los resultados se pueden usar como código base para realizar un refinamiento basado en las necesidades de desarrollo de back-end.

SELECT * FROM pgr_degree(
  $$SELECT id FROM edges WHERE id < 17$$,
  $$SELECT id, in_edges, out_edges FROM vertices$$,
  dryrun => true);
NOTICE:
    WITH

    -- a sub set of edges of the graph goes here
    g_edges AS (
      SELECT id FROM edges WHERE id < 17
    ),

    -- sub set of vertices of the graph goes here
    all_vertices AS (
      SELECT id, in_edges, out_edges FROM vertices
    ),

    g_vertices AS (
      SELECT id,
        unnest(
          coalesce(in_edges::BIGINT[], '{}'::BIGINT[])
          ||
          coalesce(out_edges::BIGINT[], '{}'::BIGINT[])) AS eid
      FROM all_vertices
    ),

    totals AS (
      SELECT v.id, count(*)
      FROM g_vertices v
      JOIN g_edges e ON (v.eid = e.id) GROUP BY v.id
    )

    SELECT id::BIGINT, count::BIGINT FROM all_vertices JOIN totals USING (id)
    ;
 node | degree
------+--------
(0 rows)

Encontrando callejones sin salida

Si se tiene una tabla de vértices ya construida usando pgr_extractVertices y se quiere el grado de todo el grafo en lugar de un subconjunto, se puede trabajar con las columnas in_edges y out_edges directamente.

El grado de un sin salida es 1.

Para obtener los callejones sin salida:

SELECT id FROM vertices
WHERE array_length(in_edges || out_edges, 1) = 1;
 id
----
  1
  5
  9
  2
  4
 13
 14
(7 rows)

Un callejón sin salida se produce cuando

• El vértice es el límite de un callejón sin salida, una vía de no paso o una vía de no salida.

• El vértice esta en el limite del grafo importado.

  • Si se importa un grafo más grande, puede que el vértice no sea un callejón sin salida.

El nodo $4$, es un callejón sin salida en la consulta, aunque visualmente parezca un punto final de 3 aristas.

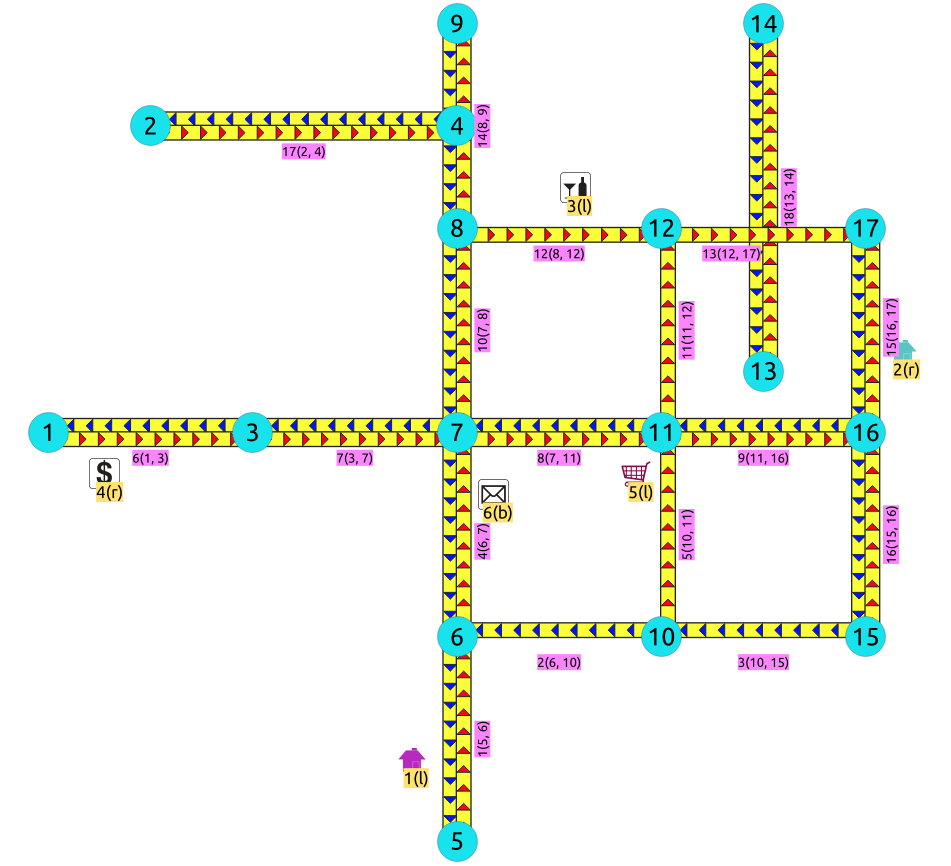
¿Es el nodo $4$ un callejón sin salida o no?

La respuesta a esta pregunta dependerá de la aplicación.

• Hay un bordillo tan pequeño:

  • ¿Eso no permite a un vehículo utilizar esa intersección visual?

  • ¿Es la aplicación para peatones y por lo tanto el peatón puede caminar fácilmente en una acera pequeña?

  • ¿Es la aplicación para la electricidad y las líneas eléctricas que se puede extender fácilmente en la parte superior de la acera pequeña?

• ¿Hay un gran acantilado y desde la vista de las águilas parece que el callejón sin salida está cerca del segmento?

Dependiendo de la respuesta, será necesario la modificación de datos.

Cuando hay muchos callejones sin salida, para acelerar el procesamiento, se pueden utilizar las funciones de Contraction - Familia de funciones para contraer el grafo.

Encontrando vértices lineales

El grado de un vértice lineal es 2.

Cuando hay una tabla de vértices construida usando pgr_extractVertices

Para obtener las aristas lineales:

SELECT id FROM vertices
WHERE array_length(in_edges || out_edges, 1) = 2;
 id
----
  3
 15
 17
(3 rows)

Estos vértices lineales son correctos, por ejemplo, cuando esos vértices son badenes, señales de alto y la aplicación los tiene en cuenta.

Cuando hay muchas aristas lineales, que no necesitan tomarse en cuenta, para acelerar el procesamiento se pueden utilizar las funciones Contraction - Familia de funciones para contraer el grafo.

Ver también

• Topología - Familia de Funciones

• pgr_extractVertices

Índices y tablas

• Índice

• Página de Búsqueda