The problem definition
Connected components
A connected component of an undirected graph is a set of vertices that are all reachable
from each other.
Notice: This problem defines on an undirected graph.
Given the following query:
pgr_connectedComponentsV(sql)
where sql={(idi,sourcei,targeti,costi,reverse_costi)}
and
- source=⋃sourcei,
- target=⋃targeti,
The graphs are defined as follows:
The weighted undirected graph, G(V,E), is definied by:
- the set of vertices V
- the set of edges E
- E={ {(sourcei,targeti,costi) when cost>=0} ∪{(targeti,sourcei,costi) when cost>=0} if reverse_cost=∅ {(sourcei,targeti,costi) when cost>=0} ∪{(targeti,sourcei,costi) when cost>=0} ∪{(targeti,sourcei,reverse_costi) when reverse_costi>=0)} ∪{(sourcei,targeti,reverse_costi) when reverse_costi>=0)} if reverse_cost≠∅
Given:
Then:
\boldsymbol{\pi} = \{(component_i, n\_seq_i, node_i)\}
- where:
- component_i = \min \{node_j | node_j \in component_i\}
- n\_seq_i is a sequential value starting from 1 in a component.
- node_i \in component_i
- The returned values are ordered:
- component ascending
- node ascending
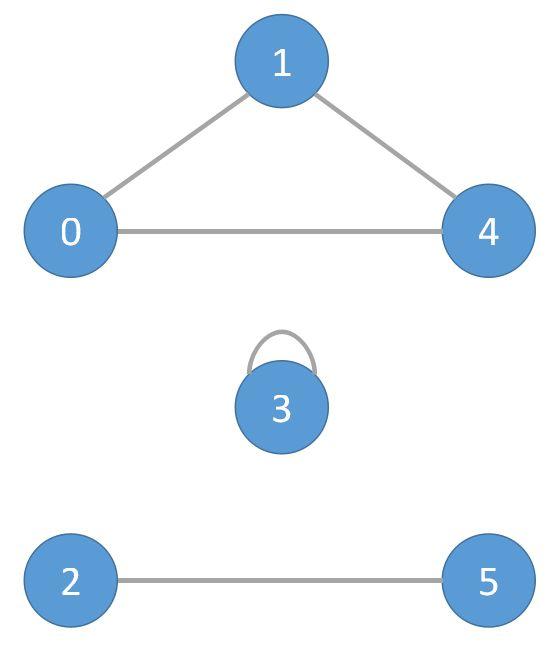
- Example:
- The first component is composed of nodes
0, 1 and 4.
- The second component is composed of node
3.
- The third component is composed of nodes
2 and 5.
Strongly connected components
A strongly connected component of a directed graph is a set of vertices that are all reachable
from each other.
Notice: This problem defines on a directed graph.
Given the following query:
pgr_strongComponentsV(sql)
where sql = \{(id_i, source_i, target_i, cost_i, reverse\_cost_i)\}
and
- source = \bigcup source_i,
- target = \bigcup target_i,
The graphs are defined as follows:
The weighted directed graph, G_d(V,E), is definied by:
- the set of vertices V
- V = source \cup target \cup {start_{vid}} \cup {end_{vid}}
- the set of edges E
- E = \begin{cases}
\text{ } \{(source_i, target_i, cost_i) \text{ when } cost >=0 \} & \quad \text{ if } reverse\_cost = \varnothing \\
\text{ } \text{ } & \text{ } \\
\text{ } \{(source_i, target_i, cost_i) \text{ when } cost >=0 \} & \text{ } \\
\cup \{(target_i, source_i, reverse\_cost_i) \text{ when } reverse\_cost_i >=0)\} & \quad \text{ if } reverse\_cost \neq \varnothing \\
\end{cases}
Given:
Then:
\boldsymbol{\pi} = \{(component_i, n\_seq_i, node_i)\}
- where:
- component_i = \min {node_j | node_j \in component_i}
- n\_seq_i is a sequential value starting from 1 in a component.
- node_i \in component_i
- The returned values are ordered:
- component ascending
- node ascending
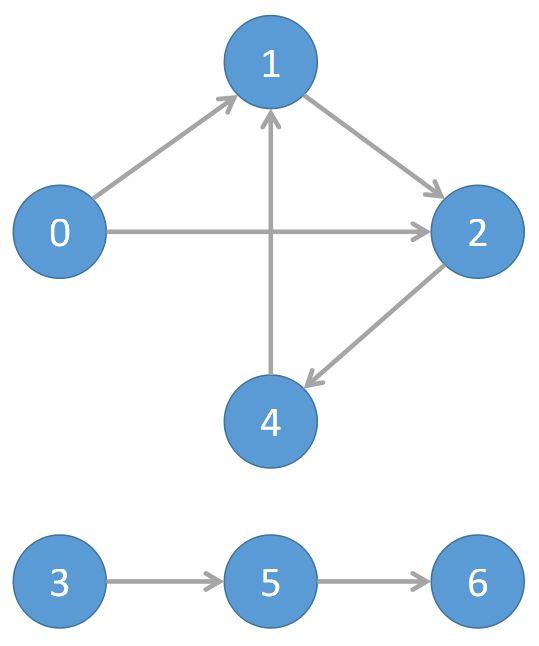
- Example:
- The first component is composed of nodes
1, 2 and 4.
- The second component is composed of node
0.
- The third component is composed of node
3.
- The fourth component is composed of node
5.
- The fifth component is composed of node
6.
Biconnected components
The biconnected components of an undirected graph are the maximal subsets of vertices such that the removal of a vertex from
particular component will not disconnect the component. Unlike connected components, vertices may belong to multiple biconnected
components. Vertices can be present in multiple biconnected components, but each edge can only be contained in a single biconnected
component. So, the output only has edge version.
Notice: This problem defines on an undirected graph.
Given the following query:
pgr_biconnectedComponents(sql)
where sql = \{(id_i, source_i, target_i, cost_i, reverse\_cost_i)\}
and
- source = \bigcup source_i,
- target = \bigcup target_i,
The graphs are defined as follows:
The weighted undirected graph, G(V,E), is definied by:
- the set of vertices V
- the set of edges E
- E = \begin{cases}
\text{ } \{(source_i, target_i, cost_i) \text{ when } cost >=0 \} & \quad \text{ } \\
\cup \{(target_i, source_i, cost_i) \text{ when } cost >=0 \} & \quad \text{ if } reverse\_cost = \varnothing \\
\text{ } \text{ } & \text{ } \\
\text{ } \{(source_i, target_i, cost_i) \text{ when } cost >=0 \} & \text{ } \\
\cup \{(target_i, source_i, cost_i) \text{ when } cost >=0 \} & \text{ } \\
\cup \{(target_i, source_i, reverse\_cost_i) \text{ when } reverse\_cost_i >=0)\} & \text{ } \\
\cup \{(source_i, target_i, reverse\_cost_i) \text{ when } reverse\_cost_i >=0)\} & \quad \text{ if } reverse\_cost \neq \varnothing \\
\end{cases}
Given:
Then:
\boldsymbol{\pi} = \{(component_i, n\_seq_i, node_i)\}
- where:
- component_i = \min {node_j | node_j \in component_i}
- n\_seq_i is a sequential value starting from 1 in a component.
- edge_i \in component_i
- The returned values are ordered:
- component ascending
- edge ascending
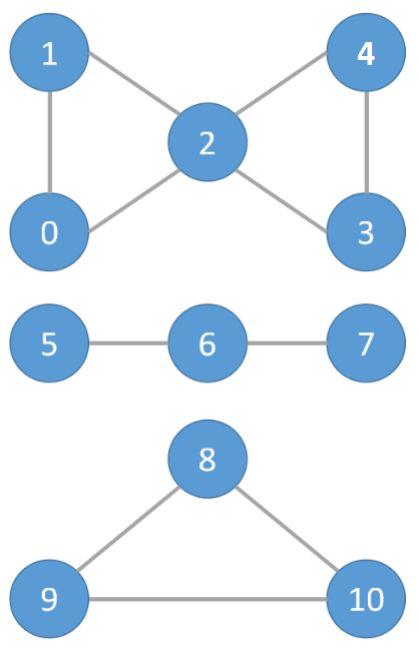
- Example:
- The first component is composed of edges
1 - 2, 0 - 1 and 0 - 2.
- The second component is composed of edges
2 - 4, 2 - 3 and 3 - 4.
- The third component is composed of edge
5 - 6.
- The fourth component is composed of edge
6 - 7.
- The fifth component is composed of edges
8 - 9, 9 - 10 and 8 - 10.
Articulation Points
Those vertices that belong to more than one biconnected component are called
articulation points or, equivalently, cut vertices. Articulation points are
vertices whose removal would increase the number of connected components in
the graph.
Notice: This problem defines on an undirected graph.
Given the following query:
pgr_articulationPoints(sql)
where sql = \{(id_i, source_i, target_i, cost_i, reverse\_cost_i)\}
and
- source = \bigcup source_i,
- target = \bigcup target_i,
The graphs are defined as follows:
The weighted undirected graph, G(V,E), is definied by:
- the set of vertices V
- the set of edges E
- E = \begin{cases}
\text{ } \{(source_i, target_i, cost_i) \text{ when } cost >=0 \} & \quad \text{ } \\
\cup \{(target_i, source_i, cost_i) \text{ when } cost >=0 \} & \quad \text{ if } reverse\_cost = \varnothing \\
\text{ } \text{ } & \text{ } \\
\text{ } \{(source_i, target_i, cost_i) \text{ when } cost >=0 \} & \text{ } \\
\cup \{(target_i, source_i, cost_i) \text{ when } cost >=0 \} & \text{ } \\
\cup \{(target_i, source_i, reverse\_cost_i) \text{ when } reverse\_cost_i >=0)\} & \text{ } \\
\cup \{(source_i, target_i, reverse\_cost_i) \text{ when } reverse\_cost_i >=0)\} & \quad \text{ if } reverse\_cost \neq \varnothing \\
\end{cases}
Given:
Then:
\boldsymbol{\pi} = \{node_i\}
- where:
- node_i is an articulation point.
- The returned values are ordered:
- Example:
- Articulation points are nodes
2 and 6.

Bridges
A bridge is an edge of an undirected graph whose deletion increases its number
of connected components.
Notice: This problem defines on an undirected graph.
Given the following query:
pgr_bridges(sql)
where sql = \{(id_i, source_i, target_i, cost_i, reverse\_cost_i)\}
and
- source = \bigcup source_i,
- target = \bigcup target_i,
The graphs are defined as follows:
The weighted undirected graph, G(V,E), is definied by:
- the set of vertices V
- the set of edges E
- E = \begin{cases}
\text{ } \{(source_i, target_i, cost_i) \text{ when } cost >=0 \} & \quad \text{ } \\
\cup \{(target_i, source_i, cost_i) \text{ when } cost >=0 \} & \quad \text{ if } reverse\_cost = \varnothing \\
\text{ } \text{ } & \text{ } \\
\text{ } \{(source_i, target_i, cost_i) \text{ when } cost >=0 \} & \text{ } \\
\cup \{(target_i, source_i, cost_i) \text{ when } cost >=0 \} & \text{ } \\
\cup \{(target_i, source_i, reverse\_cost_i) \text{ when } reverse\_cost_i >=0)\} & \text{ } \\
\cup \{(source_i, target_i, reverse\_cost_i) \text{ when } reverse\_cost_i >=0)\} & \quad \text{ if } reverse\_cost \neq \varnothing \\
\end{cases}
Given:
Then:
\boldsymbol{\pi} = \{edge_i\}
- where:
- edge_i is an edge.
- The returned values are ordered:
- Example:
- Bridges are edges
5 <--> 6 and 6 <--> 7.

Description of the edges_sql query for components functions
| edges_sql: | an SQL query, which should return a set of rows with the following columns: |
|---|
| Column |
Type |
Default |
Description |
|---|
| id |
ANY-INTEGER |
|
Identifier of the edge. |
| source |
ANY-INTEGER |
|
Identifier of the first end point vertex of the edge. |
| target |
ANY-INTEGER |
|
Identifier of the second end point vertex of the edge. |
| cost |
ANY-NUMERICAL |
|
Weight of the edge (source, target)
- When negative: edge (source, target) does not exist, therefore it’s not part of the graph.
|
| reverse_cost |
ANY-NUMERICAL |
-1 |
Weight of the edge (target, source),
- When negative: edge (target, source) does not exist, therefore it’s not part of the graph.
|
Where:
| ANY-INTEGER: | SMALLINT, INTEGER, BIGINT |
|---|
| ANY-NUMERICAL: | SMALLINT, INTEGER, BIGINT, REAL, FLOAT |
|---|
Description of the parameters of the signatures
| Parameter |
Type |
Default |
Description |
|---|
| edges_sql |
TEXT |
|
SQL query as described above. |
Description of the return values for connected components and strongly connected components
Returns set of (seq, component, n_seq, node)
| Column |
Type |
Description |
|---|
| seq |
INT |
Sequential value starting from 1. |
| component |
BIGINT |
Component identifier. It is equal to the minimum node identifier in the component. |
| n_seq |
INT |
It is a sequential value starting from 1 in a component. |
| node |
BIGINT |
Identifier of the vertex. |
Description of the return values for biconnected components, connected components (edge version) and strongly connected components
Returns set of (seq, component, n_seq, edge)
| Column |
Type |
Description |
|---|
| seq |
INT |
Sequential value starting from 1. |
| component |
BIGINT |
Component identifier. It is equal to the minimum edge identifier in the component. |
| n_seq |
INT |
It is a sequential value starting from 1 in a component. |
| edge |
BIGINT |
Identifier of the edge. |
Description of the return values for articulation points
Returns set of (seq, node)
| Column |
Type |
Description |
|---|
| seq |
INT |
Sequential value starting from 1. |
| node |
BIGINT |
Identifier of the vertex. |
Description of the return values for bridges
Returns set of (seq, node)
| Column |
Type |
Description |
|---|
| seq |
INT |
Sequential value starting from 1. |
| edge |
BIGINT |
Identifier of the edge. |
 pgRouting
v2.6.3
pgRouting
v2.6.3

