Versiones no soportadas:2.6 2.5 2.4 2.3
Supported versions:
pgr_TSPeuclidean¶
pgr_TSPeuclidean- Aproximación usando el algoritmo metric.

Adentro: Boost Graph¶
Disponibilidad:
Versión 3.2.1
Algoritmo Metrico de la Librería Boost
El algoritmo de recocido simulado ya no es utilizado
Se ignoran los parámetros relacionados con el algoritmo de recocido simulado: max_processing_time, tries_per_temperature, max_changes_per_temperature, max_consecutive_non_changes, initial_temperature, final_temperature, cooling_factor, randomize
Versión 3.0.0
Cambio de nombre de pgr_eucledianTSP
Versión 2.3.0
Nueva función Oficial
Descripción¶
Definición del Problema¶
En el problema del vendedor viajante (TSP) hace la siguiente pregunta:
Dada una lista de ciudades y las distancias entre cada par de ciudades, que corresponde con la ruta más corta posible que para visite cada ciudad exactamente una vez y regrese a la ciudad de origen?
Características¶
Este problema es un problema de optimización NP-duro.
Se utiliza el algoritmo métrico
La implementación genera soluciones que son el doble de largas que el recorrido óptimo en el peor de los casos cuando:
El grafo es no dirigido
El grafo está completamente conectado
Grafo donde los costos de viaje en los segmentos cumplen con la desigualdad del triángulo.
En un grafo no dirigido:
Los costos del viaje son simétricos:
Los costos del viaje de
uavson tanto como viajar devau
- Cualquier identificador duplicado será ignorado. Las coordenadas que se mantendrán
es arbitrario.
Las coordenadas son bastante similares para el mismo identificador, por ejemplo:
1, 3.5, 1 1, 3.499999999999 0.9999999
Las coordenadas son bastante diferentes para el mismo identificador, por ejemplo:
2, 3.5, 1.0 2, 3.6, 1.1
Firmas¶
Resumen
[start_id, end_id])(seq, node, cost, agg_cost)- Ejemplo:
Con valores predeterminados
SELECT * FROM pgr_TSPeuclidean(
$$
SELECT id, st_X(geom) AS x, st_Y(geom)AS y FROM vertices
$$);
seq | node | cost | agg_cost
-----+------+----------------+---------------
1 | 1 | 0 | 0
2 | 6 | 2.2360679775 | 2.2360679775
3 | 5 | 1 | 3.2360679775
4 | 10 | 1.41421356237 | 4.65028153987
5 | 7 | 1.41421356237 | 6.06449510225
6 | 2 | 2.12132034356 | 8.18581544581
7 | 9 | 1.58113883008 | 9.76695427589
8 | 4 | 0.5 | 10.2669542759
9 | 14 | 1.58113883009 | 11.848093106
10 | 17 | 1.11803398875 | 12.9661270947
11 | 16 | 1 | 13.9661270947
12 | 15 | 1 | 14.9661270947
13 | 11 | 1.41421356237 | 16.3803406571
14 | 13 | 0.583095189485 | 16.9634358466
15 | 12 | 0.860232526704 | 17.8236683733
16 | 8 | 1 | 18.8236683733
17 | 3 | 1.41421356237 | 20.2378819357
18 | 1 | 1 | 21.2378819357
(18 rows)
Parámetros¶
Parámetro |
Tipo |
Descripción |
|---|---|---|
|
SQL de coordenadas descritas más adelante |
Parámetros opcionales de TSP¶
Columna |
Tipo |
x Defecto |
Descripción |
|---|---|---|---|
|
ENTEROS |
|
El primer vértice visitado
|
|
ENTEROS |
|
Último vértice visitado antes de regresar a
|
Consultas Internas¶
Coordenadas SQL¶
Coordinates SQL: an SQL query, which should return a set of rows with the following columns:
Columna |
Tipo |
Descripción |
|---|---|---|
id |
|
Identificador del vértice de salida. |
x |
|
Valor X de la coordenada. |
y |
|
Valor Y de la coordenada. |
Columnas de Resultados¶
Devuelve el CONJUNTO DE (seq, node, cost, agg_cost)
Columna |
Tipo |
Descripción |
|---|---|---|
|
|
Secuencia de filas. |
node |
|
Identificador del nodo/coordenada/punto. |
costo |
|
Coste que se debe recorrer desde el
|
|
|
Costo agregado del
|
Ejemplos Adicionales¶
Prueba 29 ciudades del Sáhara Occidental¶
Este ejemplo muestra cómo hacer pruebas de rendimiento utilizando los datos de ejemplo de la Universidad de Waterloo utilizando el conjunto de datos de 29 ciudades del Sáhara Occidental
Creación de una tabla para datos y almacenamiento de los datos¶
CREATE TABLE wi29 (id BIGINT, x FLOAT, y FLOAT, geom geometry);
INSERT INTO wi29 (id, x, y) VALUES
(1,20833.3333,17100.0000),
(2,20900.0000,17066.6667),
(3,21300.0000,13016.6667),
(4,21600.0000,14150.0000),
(5,21600.0000,14966.6667),
(6,21600.0000,16500.0000),
(7,22183.3333,13133.3333),
(8,22583.3333,14300.0000),
(9,22683.3333,12716.6667),
(10,23616.6667,15866.6667),
(11,23700.0000,15933.3333),
(12,23883.3333,14533.3333),
(13,24166.6667,13250.0000),
(14,25149.1667,12365.8333),
(15,26133.3333,14500.0000),
(16,26150.0000,10550.0000),
(17,26283.3333,12766.6667),
(18,26433.3333,13433.3333),
(19,26550.0000,13850.0000),
(20,26733.3333,11683.3333),
(21,27026.1111,13051.9444),
(22,27096.1111,13415.8333),
(23,27153.6111,13203.3333),
(24,27166.6667,9833.3333),
(25,27233.3333,10450.0000),
(26,27233.3333,11783.3333),
(27,27266.6667,10383.3333),
(28,27433.3333,12400.0000),
(29,27462.5000,12992.2222);
Agregar una geometría (con fines visuales)¶
UPDATE wi29 SET geom = ST_makePoint(x,y);
Costo total del tour¶
Al obtener un costo total del recorrido, comparar el valor con la duración de un recorrido óptimo, que es 27603, dado en el conjunto de datos
SELECT *
FROM pgr_TSPeuclidean($$SELECT * FROM wi29$$)
WHERE seq = 30;
seq | node | cost | agg_cost
-----+------+---------------+---------------
30 | 1 | 2266.91173136 | 28777.4854127
(1 row)
Obtener una geometría del recorrido¶
WITH
tsp_results AS (SELECT seq, geom FROM pgr_TSPeuclidean($$SELECT * FROM wi29$$) JOIN wi29 ON (node = id))
SELECT ST_MakeLine(ARRAY(SELECT geom FROM tsp_results ORDER BY seq));
st_makeline
--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
01020000001E000000F085C9545558D4400000000000B3D040000000000069D440107A36ABAAAAD040000000000018D54000000000001DD040107A36AB2A10D7401FF46C5655FDCE40000000000025D740E10B93A9AA1ECF40F085C954D552D740E10B93A9AA62CC40107A36ABAA99D7400000000000E1C940107A36AB4A8FD840E10B93A9EA26C840F085C954D5AAD9401FF46C5655EFC840F085C95455D0D940E10B93A9AA3CCA40F085C9545585D940000000000052CC400000000080EDD94000000000000DCB40A52C431C0776DA40E10B93A9EA33CA40A52C431C6784DA40E10B93A9AAC9C940A52C431C8764DA402C6519E2F87DC94000000000A0D1DA4096B20C711C60C940F085C95455CADA40000000000038C840F085C9545598DA40E10B93A9AA03C740F085C954551BDA40E10B93A9AAD1C640F085C9545598DA40000000000069C440107A36ABAAA0DA40E10B93A9AA47C440107A36ABAA87DA40E10B93A9AA34C340000000008089D94000000000009BC440F085C954D526D6401FF46C5655D6C840F085C954D5A9D540E10B93A9AAA6C9400000000000CDD4401FF46C56556CC940000000000018D5400000000000A3CB40F085C954D50DD6400000000000EECB40000000000018D5401FF46C56553BCD40F085C9545558D4400000000000B3D040
(1 row)
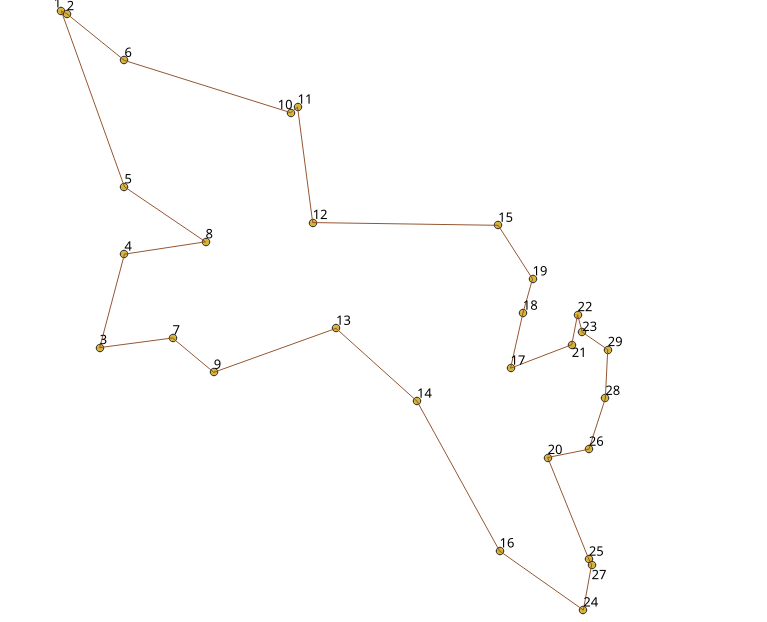
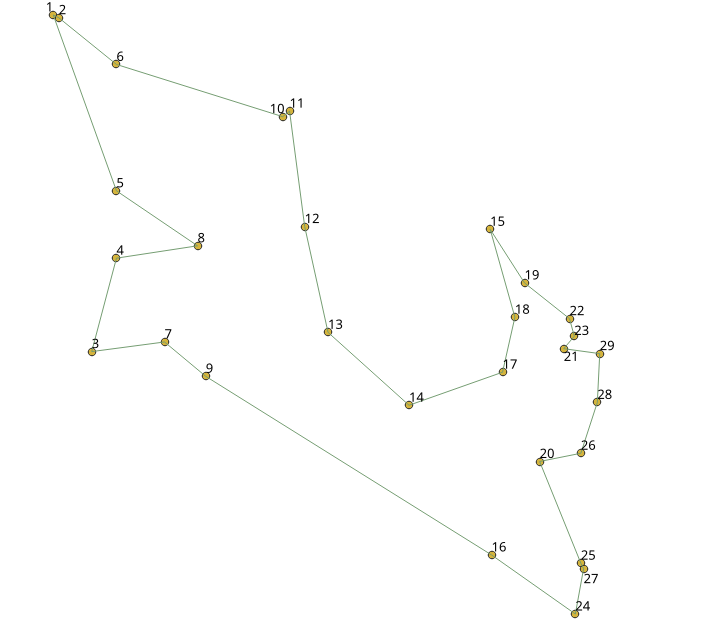
Resultados visuales¶
Visualmente, la primera imagen es la “solución óptima”<https://www.math.uwaterloo.ca/tsp/world/witour.html>`__ y la segunda imagen es la solución obtenida con pgr_TSPeuclidean.
Ver también¶
Índices y tablas
