• Supported versions:

Conceptos de pgRouting

Esta es una guía simple que va a través de los pasos básicos para empezar trabajar con pgRouting. Esta guía cubre:

Graphs

Definición de grafo

A graph is an ordered pair \(G = (V ,E)\) where:

• \(V\) is a set of vertices, also called nodes.

• \(E \subseteq \{( u, v ) \mid u , v \in V \}\)

There are different kinds of graphs:

• Grafo no dirigido

  • \(E \subseteq \{( u, v ) \mid u , v \in V\}\)

• Undirected simple graph

  • \(E \subseteq \{( u, v ) \mid u , v \in V, u \neq v\}\)

• Grafo dirigido

  • \(E \subseteq \{( u, v ) \mid (u , v) \in (V X V) \}\)

• Directed simple graph

  • \(E \subseteq \{( u, v ) \mid (u , v) \in (V X V), u \neq v\}\)

Graphs:

• Do not have geometries.

• Some graph theory problems require graphs to have weights, called cost in pgRouting.

In pgRouting there are several ways to represent a graph on the database:

• With cost

  • (id, source, target, cost)

• With cost and reverse_cost

  • (id, source, target, cost, reverse_cost)

Donde:

Columna	Descripción
id	Identifier of the edge. Requirement to use the database in a consistent. manner.
source	Identificador de un vértice.
target	Identificador de un vértice.
cost	Peso de la arista (source, target): Cuando negativo: la arista (source, target) no existe en el grafo. cost must exist in the query.
reverse_cost	Peso de la arista (target, source) Cuando negativo: la arista (target, source) no existe en el grafo.

The decision of the graph to be directed or undirected is done when executing a pgRouting algorithm.

Graph with cost

The weighted directed graph, \(G_d(V,E)\):

• Graph data is obtained with a query

  SELECT id, source, target, cost FROM edges

• El conjunto de aristas \(E\)

  • \(E = \{(source_{id}, target_{id}, cost_{id}) \text{ when } cost_{id} \ge 0 \}\)

  • Edges where cost is non negative are part of the graph.

• Conjunto de vértices \(V\)

  • \(V = \{source_{id} \cup target_{id}\}\)

  • All vertices in source and target are part of the graph.

Grafo dirigido

In a directed graph the edge \((source_{id}, target_{id}, cost_{id})\) has directionality: \(source_{id} \rightarrow target_{id}\)

For the following data:

SELECT *
FROM (VALUES (1, 1, 2, 5), (2, 1, 3, -3))
     AS t(id, source, target, cost);
 id | source | target | cost
----+--------+--------+------
  1 |      1 |      2 |    5
  2 |      1 |      3 |   -3
(2 rows)

Edge \(2\) (\(1 \rightarrow 3\)) is not part of the graph.

The data is representing the following graph:

Grafo no dirigido

In an undirected graph the edge \((source_{id}, target_{id}, cost_{id})\) does not have directionality: \(source_{id} \frac{\;\;\;\;\;}{} target_{id}\)

• In terms of a directed graph is like having two edges: \(source_{id} \leftrightarrow target_{id}\)

For the following data:

SELECT *
FROM (VALUES (1, 1, 2, 5), (2, 1, 3, -3))
     AS t(id, source, target, cost);
 id | source | target | cost
----+--------+--------+------
  1 |      1 |      2 |    5
  2 |      1 |      3 |   -3
(2 rows)

Edge \(2\) (\(1 \frac{\;\;\;\;\;}{} 3\)) is not part of the graph.

The data is representing the following graph:

Graph with cost and reverse_cost

The weighted directed graph, \(G_d(V,E)\), is defined by:

• Graph data is obtained with a query

  SELECT id, source, target, cost, reverse_cost FROM edges

• The set of edges \(E\):

  • \(E = \begin{split} \begin{align} & {\{(source_{id}, target_{id}, cost_{id}) \text{ when } cost_{id} >=0 \}} \\ & \cup \\ & {\{(target_{id}, source_{id}, reverse\_cost_{id}) \text{ when } reverse\_cost_{id} >=0 \}} \end{align} \end{split}\)

  • Edges \((source \rightarrow target)\) where cost is non negative are part of the graph.

  • Edges \((target \rightarrow source)\) where reverse_cost is non negative are part of the graph.

• The set of vertices \(V\):

  • \(V = \{source_{id} \cup target_{id}\}\)

  • All vertices in source and target are part of the graph.

Grafo dirigido

In a directed graph both edges have directionality

• edge \((source_{id}, target_{id}, cost_{id})\) has directionality: \(source_{id} \rightarrow target_{id}\)

• edge \((target_{id}, source_{id}, reverse\_cost_{id})\) has directionality: \(target_{id} \rightarrow source_{id}\)

For the following data:

SELECT *
FROM (VALUES (1, 1, 2, 5, 2), (2, 1, 3, -3, 4), (3, 2, 3, 7, -1))
     AS t(id, source, target, cost, reverse_cost);
 id | source | target | cost | reverse_cost
----+--------+--------+------+--------------
  1 |      1 |      2 |    5 |            2
  2 |      1 |      3 |   -3 |            4
  3 |      2 |      3 |    7 |           -1
(3 rows)

Edges not part of the graph:

• \(2\) (\(1 \rightarrow 3\))

• \(3\) (\(3 \rightarrow 2\))

The data is representing the following graph:

Grafo no dirigido

In a directed graph both edges do not have directionality

• Edge \((source_{id}, target_{id}, cost_{id})\) is \(source_{id} \frac{\;\;\;\;\;}{} target_{id}\)

• Edge \((target_{id}, source_{id}, reverse\_cost_{id})\) is \(target_{id} \frac{\;\;\;\;\;}{} source_{id}\)

• In terms of a directed graph is like having four edges:

  • \(source_i \leftrightarrow target_i\)

  • \(target_i \leftrightarrow source_i\)

For the following data:

SELECT *
FROM (VALUES (1, 1, 2, 5, 2), (2, 1, 3, -3, 4), (3, 2, 3, 7, -1))
     AS t(id, source, target, cost, reverse_cost);
 id | source | target | cost | reverse_cost
----+--------+--------+------+--------------
  1 |      1 |      2 |    5 |            2
  2 |      1 |      3 |   -3 |            4
  3 |      2 |      3 |    7 |           -1
(3 rows)

Edges not part of the graph:

• \(2\) (\(1 \frac{\;\;\;\;\;}{} 3\))

• \(3\) (\(3 \frac{\;\;\;\;\;}{} 2\))

The data is representing the following graph:

Graphs without geometries

Personal relationships, genealogy, file dependency problems can be solved using pgRouting. Those problems, normally, do not come with geometries associated with the graph.

Ejemplo de Wiki

Solve the example problem taken from wikipedia):

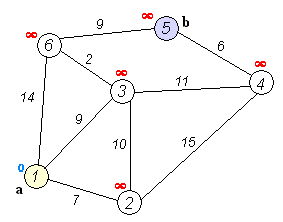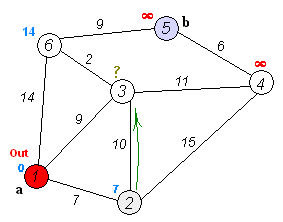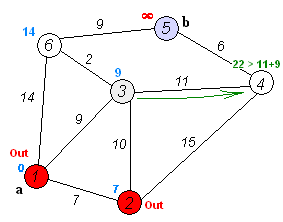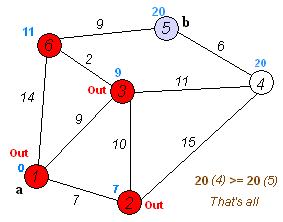
Donde:

• Problem is to find the shortest path from \(1\) to \(5\).

• Is an undirected graph.

• Although visually looks like to have geometries, the drawing is not to scale.

  • No geometries associated to the vertices or edges

• Has 6 vertices \(\{1,2,3,4,5,6\}\)

• Has 9 edges:

  \(\begin{split} \begin{align} E = & \{(1,2,7), (1,3,9), (1,6,14), \\ & (2,3,10), (2,4,13), \\ & (3,4,11), (3,6,2), \\ & (4,5,6), \\ & (5,6,9) \} \end{align} \end{split}\)

• The graph can be represented in many ways for example:

Prepare the database

Create a database for the example, access the database and install pgRouting:

$ createdb wiki
$ psql wiki
wiki =# CREATE EXTENSION pgRouting CASCADE;

Crear una tabla

The basic elements needed to perform basic routing on an undirected graph are:

Columna	Tipo	Descripción
id	ENTEROS	Identificador de la arista.
source	ENTEROS	Identificador del primer vértice de la arista.
target	ENTEROS	Identificador del segundo vértice de la arista.
cost	FLOTANTES	Peso de la arista (source, target)

Donde:

ENTEROS:

SMALLINT, INTEGER, BIGINT

FLOTANTES:

SMALLINT, INTEGER, BIGINT, REAL, FLOAT

Using this table design for this example:

CREATE TABLE wiki (
  id SERIAL,
  source INTEGER,
  target INTEGER,
  cost INTEGER);
CREATE TABLE

Insert the data

INSERT INTO wiki (source, target, cost) VALUES
(1, 2, 7),  (1, 3, 9), (1, 6, 14),
(2, 3, 10), (2, 4, 15),
(3, 6, 2),  (3, 4, 11),
(4, 5, 6),
(5, 6, 9);
INSERT 0 9

Find the shortest path

To solve this example pgr_dijkstra is used:

SELECT * FROM pgr_dijkstra(
  'SELECT id, source, target, cost FROM wiki',
  1, 5, false);
 seq | path_seq | node | edge | cost | agg_cost
-----+----------+------+------+------+----------
   1 |        1 |    1 |    2 |    9 |        0
   2 |        2 |    3 |    6 |    2 |        9
   3 |        3 |    6 |    9 |    9 |       11
   4 |        4 |    5 |   -1 |    0 |       20
(4 rows)

To go from \(1\) to \(5\) the path goes thru the following vertices: \(1 \rightarrow 3 \rightarrow 6 \rightarrow 5\)

Información de vertices

To obtain the vertices information, use pgr_extractVertices – Propuesto

SELECT id, in_edges, out_edges
FROM pgr_extractVertices('SELECT id, source, target FROM wiki');
 id | in_edges | out_edges
----+----------+-----------
  3 | {2,4}    | {6,7}
  5 | {8}      | {9}
  4 | {5,7}    | {8}
  2 | {1}      | {4,5}
  1 |          | {1,2,3}
  6 | {3,6,9}  |
(6 rows)

Graphs with geometries

Crear una Base de Datos de Ruteo

The first step is to create a database and load pgRouting in the database.

Typically create a database for each project.

Once having the database to work in, load your data and build the routing application in that database.

createdb sampledata
psql sampledata -c "CREATE EXTENSION pgrouting CASCADE"

Cargar Datos

There are several ways to load your data into pgRouting.

• Manually creating a database.

  • Graphs without geometries

  • Datos Muestra: a small graph used on the documentation examples

• Using osm2pgrouting

Existen varias herramientas de codigo abierto que pueden ayudar, como:

shp2pgsql:

• cargador a postgresql de archivos shape

ogr2ogr:

• herramienta de conversión de datos vectoriales

osm2pgsql:

• cargar datos de OSM a postgresql

Tener en cuenta que estas herramientas no importan los datos a una estructura compatible con pgRouting y cuando esto sucede, la topología necesita ser ajustada.

• Breakup a segments on each segment-segment intersection

• When missing, add columns and assign values to source, target, cost, reverse_cost.

• Connect a disconnected graph.

• Create the complete graph topology

• Create one or more graphs based on the application to be developed.

  • Create a contracted graph for the high speed roads

  • Create graphs per state/country

In few words:

Prepare the graph

What and how to prepare the graph, will depend on the application and/or on the quality of the data and/or on how close the information is to have a topology usable by pgRouting and/or some other factors not mentioned.

The steps to prepare the graph involve geometry operations using PostGIS and some others involve graph operations like pgr_contraction to contract a graph.

The workshop has a step by step on how to prepare a graph using Open Street Map data, for a small application.

The use of indexes on the database design in general:

• Have the geometries indexed.

• Have the identifiers columns indexed.

Please consult the PostgreSQL documentation and the PostGIS documentation.

Construir una topología de ruteo

The basic information to use the majority of the pgRouting functions id, source, target, cost, [reverse_cost] is what in pgRouting is called the routing topology.

reverse_cost is optional but strongly recommended to have in order to reduce the size of the database due to the size of the geometry columns. Having said that, in this documentation reverse_cost is used in this documentation.

When the data comes with geometries and there is no routing topology, then this step is needed.

All the start and end vertices of the geometries need an identifier that is to be stored in a source and target columns of the table of the data. Likewise, cost and reverse_cost need to have the value of traversing the edge in both directions.

If the columns do not exist they need to be added to the table in question. (see ALTER TABLE)

The function pgr_extractVertices – Propuesto is used to create a vertices table based on the edge identifier and the geometry of the edge of the graph.

Finally using the data stored on the vertices tables the source and target are filled up.

See Datos Muestra for an example for building a topology.

Data coming from OSM and using osm2pgrouting as an import tool, comes with the routing topology. See an example of using osm2pgrouting on the workshop.

Adjust costs

For this example the cost and reverse_cost values are going to be the double of the length of the geometry.

Update costs to length of geometry

Suppose that cost and reverse_cost columns in the sample data represent:

• \(1\) when the edge exists in the graph

• \(-1\) when the edge does not exist in the graph

Using that information updating to the length of the geometries:

UPDATE edges SET
cost = sign(cost) * ST_length(geom) * 2,
reverse_cost = sign(reverse_cost) * ST_length(geom) * 2;
UPDATE 18

Which gives the following results:

SELECT id, cost, reverse_cost FROM edges;
 id |        cost        |    reverse_cost
----+--------------------+--------------------
  6 |                  2 |                  2
  7 |                  2 |                  2
  4 |                  2 |                  2
  5 |                  2 |                 -2
  8 |                  2 |                  2
 12 |                  2 |                 -2
 11 |                  2 |                 -2
 10 |                  2 |                  2
 17 |     2.999999999998 |     2.999999999998
 14 |                  2 |                  2
 18 | 3.4000000000000004 | 3.4000000000000004
 13 |                  2 |                 -2
 15 |                  2 |                  2
 16 |                  2 |                  2
  9 |                  2 |                  2
  3 |                 -2 |                  2
  1 |                  2 |                  2
  2 |                 -2 |                  2
(18 rows)

Note that to be able to follow the documentation examples, everything is based on the original graph.

Returning to the original data:

UPDATE edges SET
cost = sign(cost),
reverse_cost = sign(reverse_cost);
UPDATE 18

Update costs based on codes

Other datasets, can have a column with values like

• FT vehicle flow on the direction of the geometry

• TF vehicle flow opposite of the direction of the geometry

• B vehicle flow on both directions

Preparing a code column for the example:

ALTER TABLE edges ADD COLUMN direction TEXT;
ALTER TABLE
UPDATE edges SET
direction = CASE WHEN (cost>0 AND reverse_cost>0) THEN 'B'
           WHEN (cost>0 AND reverse_cost<0) THEN 'FT'
           WHEN (cost<0 AND reverse_cost>0) THEN 'TF'
           ELSE '' END;
UPDATE 18

Adjusting the costs based on the codes:

UPDATE edges SET
cost = CASE WHEN (direction = 'B' OR direction = 'FT')
       THEN ST_length(geom) * 2
       ELSE -1 END,
reverse_cost = CASE WHEN (direction = 'B' OR direction = 'TF')
       THEN ST_length(geom) * 2
       ELSE -1 END;
UPDATE 18

Which gives the following results:

SELECT id, cost, reverse_cost FROM edges;
 id |        cost        |    reverse_cost
----+--------------------+--------------------
  6 |                  2 |                  2
  7 |                  2 |                  2
  4 |                  2 |                  2
  5 |                  2 |                 -1
  8 |                  2 |                  2
 12 |                  2 |                 -1
 11 |                  2 |                 -1
 10 |                  2 |                  2
 17 |     2.999999999998 |     2.999999999998
 14 |                  2 |                  2
 18 | 3.4000000000000004 | 3.4000000000000004
 13 |                  2 |                 -1
 15 |                  2 |                  2
 16 |                  2 |                  2
  9 |                  2 |                  2
  3 |                 -1 |                  2
  1 |                  2 |                  2
  2 |                 -1 |                  2
(18 rows)

Returning to the original data:

UPDATE edges SET
cost = sign(cost),
reverse_cost = sign(reverse_cost);
UPDATE 18
ALTER TABLE edges DROP COLUMN direction;
ALTER TABLE

Compruebe la Topología de Ruteo

There are lots of possible problems in a graph.

• The data used may not have been designed with routing in mind.

• A graph has some very specific requirements.

• The graph is disconnected.

• There are unwanted intersections.

• The graph is too large and needs to be contracted.

• A sub graph is needed for the application.

• and many other problems that the pgRouting user, that is the application developer might encounter.

Crossing edges

To get the crossing edges:

SELECT a.id, b.id
FROM edges AS a, edges AS b
WHERE a.id < b.id AND st_crosses(a.geom, b.geom);
 id | id
----+----
 13 | 18
(1 row)

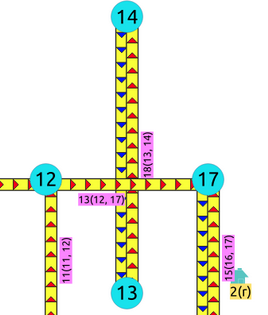
That information is correct, for example, when in terms of vehicles, is it a tunnel or bride crossing over another road.

It might be incorrect, for example:

1. When it is actually an intersection of roads, where vehicles can make turns.

2. When in terms of electrical lines, the electrical line is able to switch roads even on a tunnel or bridge.

When it is incorrect, it needs fixing:

1. For vehicles and pedestrians

   • If the data comes from OSM and was imported to the database using osm2pgrouting, the fix needs to be done in the OSM portal and the data imported again.

   • In general when the data comes from a supplier that has the data prepared for routing vehicles, and there is a problem, the data is to be fixed from the supplier

2. For very specific applications

   • The data is correct when from the point of view of routing vehicles or pedestrians.

   • The data needs a local fix for the specific application.

Once analyzed one by one the crossings, for the ones that need a local fix, the edges need to be split.

SELECT ST_AsText((ST_Dump(ST_Split(a.geom, b.geom))).geom)
FROM edges AS a, edges AS b
WHERE a.id = 13 AND b.id = 18
UNION
SELECT ST_AsText((ST_Dump(ST_Split(b.geom, a.geom))).geom)
FROM edges AS a, edges AS b
WHERE a.id = 13 AND b.id = 18;
         st_astext
---------------------------
 LINESTRING(3.5 2.3,3.5 3)
 LINESTRING(3 3,3.5 3)
 LINESTRING(3.5 3,4 3)
 LINESTRING(3.5 3,3.5 4)
(4 rows)

The new edges need to be added to the edges table, the rest of the attributes need to be updated in the new edges, the old edges need to be removed and the routing topology needs to be updated.

Adding split edges

For each pair of crossing edges a process similar to this one must be performed.

The columns inserted and the way are calculated are based on the application. For example, if the edges have a trait name, then that column is to be copied.

Para llos cálculos de pgRouting

• factor based on the position of the intersection of the edges can be used to adjust the cost and reverse_cost columns.

• Capacity information, used on the Flow - Familia de funciones functions does not need to change when splitting edges.

WITH
first_edge AS (
  SELECT (ST_Dump(ST_Split(a.geom, b.geom))).path[1],
    (ST_Dump(ST_Split(a.geom, b.geom))).geom,
    ST_LineLocatePoint(a.geom,ST_Intersection(a.geom,b.geom)) AS factor
  FROM edges AS a, edges AS b
  WHERE a.id = 13 AND b.id = 18),
first_segments AS (
  SELECT path, first_edge.geom,
    capacity, reverse_capacity,
    CASE WHEN path=1 THEN factor * cost
         ELSE (1 - factor) * cost END AS cost,
    CASE WHEN path=1 THEN factor * reverse_cost
         ELSE (1 - factor) * reverse_cost END AS reverse_cost
  FROM first_edge , edges WHERE id = 13),
second_edge AS (
  SELECT (ST_Dump(ST_Split(b.geom, a.geom))).path[1],
    (ST_Dump(ST_Split(b.geom, a.geom))).geom,
    ST_LineLocatePoint(b.geom,ST_Intersection(a.geom,b.geom)) AS factor
  FROM edges AS a, edges AS b
  WHERE a.id = 13 AND b.id = 18),
second_segments AS (
  SELECT path, second_edge.geom,
    capacity, reverse_capacity,
    CASE WHEN path=1 THEN factor * cost
         ELSE (1 - factor) * cost END AS cost,
    CASE WHEN path=1 THEN factor * reverse_cost
         ELSE (1 - factor) * reverse_cost END AS reverse_cost
  FROM second_edge , edges WHERE id = 18),
all_segments AS (
  SELECT * FROM first_segments
  UNION
  SELECT * FROM second_segments)
INSERT INTO edges
  (capacity, reverse_capacity,
    cost, reverse_cost,
    x1, y1, x2, y2,
    geom)
(SELECT capacity, reverse_capacity, cost, reverse_cost,
  ST_X(ST_StartPoint(geom)), ST_Y(ST_StartPoint(geom)),
  ST_X(ST_EndPoint(geom)), ST_Y(ST_EndPoint(geom)),
  geom
  FROM all_segments);
INSERT 0 4

Añadiendo nuevos vértices

After adding all the split edges required by the application, the newly created vertices need to be added to the vertices table.

INSERT INTO vertices (in_edges, out_edges, x, y, geom)
(SELECT nv.in_edges, nv.out_edges, nv.x, nv.y, nv.geom
FROM pgr_extractVertices('SELECT id, geom FROM edges') AS nv
LEFT JOIN vertices AS v USING(geom) WHERE v.geom IS NULL);
INSERT 0 1

Actualizar la topología de aristas

/* -- set the source information */
UPDATE edges AS e
SET source = v.id
FROM vertices AS v
WHERE source IS NULL AND ST_StartPoint(e.geom) = v.geom;
UPDATE 4
/* -- set the target information */
UPDATE edges AS e
SET target = v.id
FROM vertices AS v
WHERE target IS NULL AND ST_EndPoint(e.geom) = v.geom;
UPDATE 4

Removing the surplus edges

Once all significant information needed by the application has been transported to the new edges, then the crossing edges can be deleted.

DELETE FROM edges WHERE id IN (13, 18);
DELETE 2

There are other options to do this task, like creating a view, or a materialized view.

Actializar la topología de vértices

To keep the graph consistent, the vertices topology needs to be updated

UPDATE vertices AS v SET
in_edges = nv.in_edges, out_edges = nv.out_edges
FROM (SELECT * FROM pgr_extractVertices('SELECT id, geom FROM edges')) AS nv
WHERE v.geom = nv.geom;
UPDATE 18

Checking for crossing edges

There are no crossing edges on the graph.

SELECT a.id, b.id
FROM edges AS a, edges AS b
WHERE a.id < b.id AND st_crosses(a.geom, b.geom);
 id | id
----+----
(0 rows)

Disconnected graphs

Para obtener la conectividad del grafo:

SELECT * FROM pgr_connectedComponents(
  'SELECT id, source, target, cost, reverse_cost FROM edges'
);
 seq | component | node
-----+-----------+------
   1 |         1 |    1
   2 |         1 |    3
   3 |         1 |    5
   4 |         1 |    6
   5 |         1 |    7
   6 |         1 |    8
   7 |         1 |    9
   8 |         1 |   10
   9 |         1 |   11
  10 |         1 |   12
  11 |         1 |   13
  12 |         1 |   14
  13 |         1 |   15
  14 |         1 |   16
  15 |         1 |   17
  16 |         1 |   18
  17 |         2 |    2
  18 |         2 |    4
(18 rows)

In this example, the component \(2\) consists of vertices \(\{2, 4\}\) and both vertices are also part of the dead end result set.

This graph needs to be connected.

Nota

With the original graph of this documentation, there would be 3 components as the crossing edge in this graph is a different component.

Prepare storage for connection information

ALTER TABLE vertices ADD COLUMN component BIGINT;
ALTER TABLE
ALTER TABLE edges ADD COLUMN component BIGINT;
ALTER TABLE

Save the vertices connection information

UPDATE vertices SET component = c.component
FROM (SELECT * FROM pgr_connectedComponents(
  'SELECT id, source, target, cost, reverse_cost FROM edges'
)) AS c
WHERE id = node;
UPDATE 18

Save the edges connection information

UPDATE edges SET component = v.component
FROM (SELECT id, component FROM vertices) AS v
WHERE source = v.id;
UPDATE 20

Get the closest vertex

The closest vertex to component \(1\) is vertex \(4\). And the closest edge to vertex \(4\) is edge \(14\).

WITH
edges_sql AS (SELECT id, geom FROM edges WHERE component = 1),
point_sql AS (SELECT geom AS point FROM vertices WHERE component = 2),
results AS (
  SELECT
    id::BIGINT AS edge_id,
    ST_LineLocatePoint(geom, point) AS fraction,
    CASE WHEN ST_Intersects(ST_Buffer(geom, 2, 'side=right endcap=flat'), point)
         THEN 'r'
         ELSE 'l' END::CHAR AS side,
    geom <-> point AS distance,
    point,
    ST_MakeLine(point, ST_ClosestPoint(geom, point)) AS new_line
  FROM  edges_sql, point_sql
  WHERE ST_DWithin(geom, point, 2)
  ORDER BY geom <-> point),
prepare_cap AS (
  SELECT row_number() OVER (PARTITION BY point ORDER BY point, distance) AS rn, *
  FROM results),
cap AS (
  SELECT edge_id, fraction, side, distance, point, new_line
  FROM prepare_cap
  WHERE rn <= 1
)
SELECT edge_id, fraction, side, distance, point AS geom, new_line AS edge, id AS closest_vertex
INTO closest
FROM cap JOIN vertices ON (point = geom) ORDER BY distance LIMIT 1;
SELECT 1

The edge can be used to connect the components, using the fraction information about the edge \(14\) to split the connecting edge.

Conectando componentes

There are three basic ways to connect the components

• From the vertex to the starting point of the edge

• From the vertex to the ending point of the edge

• From the vertex to the closest vertex on the edge

  • This solution requires the edge to be split.

The following query shows the three ways to connect the components:

WITH
info AS (
  SELECT
    edge_id, fraction, side, distance, ce.geom, edge, v.id AS closest,
    source, target, capacity, reverse_capacity, e.geom AS e_geom
  FROM closest AS ce
  JOIN vertices AS v USING (geom)
  JOIN edges AS e ON (edge_id = e.id)
  ORDER BY distance LIMIT 1),
three_options AS (
  SELECT
    closest AS source, target, 0 AS cost, 0 AS reverse_cost,
    capacity, reverse_capacity,
    ST_X(geom) AS x1, ST_Y(geom) AS y1,
    ST_X(ST_EndPoint(e_geom)) AS x2, ST_Y(ST_EndPoint(e_geom)) AS y2,
    ST_MakeLine(geom, ST_EndPoint(e_geom)) AS geom
  FROM info

  UNION

  SELECT closest, source, 0, 0, capacity, reverse_capacity,
    ST_X(geom) AS x1, ST_Y(geom) AS y1,
    ST_X(ST_StartPoint(e_geom)) AS x2, ST_Y(ST_StartPoint(e_geom)) AS y2,
    ST_MakeLine(info.geom, ST_StartPoint(e_geom))
  FROM info
  /*
  UNION
  -- This option requires splitting the edge
  SELECT closest, NULL, 0, 0, capacity, reverse_capacity,
    ST_X(geom) AS x1, ST_Y(geom) AS y1,
    ST_X(ST_EndPoint(edge)) AS x2, ST_Y(ST_EndPoint(edge)) AS y2,
    edge
  FROM info */
  )

INSERT INTO edges
  (source, target,
    cost, reverse_cost,
    capacity, reverse_capacity,
    x1, y1, x2, y2,
    geom)
(SELECT
    source, target, cost, reverse_cost, capacity, reverse_capacity,
    x1, y1, x2, y2, geom
  FROM three_options);
INSERT 0 2

Checking components

Ignoring the edge that requires further work. The graph is now fully connected as there is only one component.

SELECT * FROM pgr_connectedComponents(
  'SELECT id, source, target, cost, reverse_cost FROM edges'
);
 seq | component | node
-----+-----------+------
   1 |         1 |    1
   2 |         1 |    2
   3 |         1 |    3
   4 |         1 |    4
   5 |         1 |    5
   6 |         1 |    6
   7 |         1 |    7
   8 |         1 |    8
   9 |         1 |    9
  10 |         1 |   10
  11 |         1 |   11
  12 |         1 |   12
  13 |         1 |   13
  14 |         1 |   14
  15 |         1 |   15
  16 |         1 |   16
  17 |         1 |   17
  18 |         1 |   18
(18 rows)

Contraction of a graph

The graph can be reduced in size using Contraction - Familia de funciones

When to contract will depend on the size of the graph, processing times, correctness of the data, on the final application, or any other factor not mentioned.

A fairly good method of finding out if contraction can be useful is because of the number of dead ends and/or the number of linear edges.

A complete method on how to contract and how to use the contracted graph is described on Contraction - Familia de funciones

Callejones sin salida

To get the dead ends:

SELECT id FROM vertices
WHERE array_length(in_edges || out_edges, 1) = 1;
 id
----
  1
  5
  9
 13
 14
  2
  4
(7 rows)

That information is correct, for example, when the dead end is on the limit of the imported graph.

Visually node \(4\) looks to be as start/ending of 3 edges, but it is not.

Is that correct?

• Is there such a small curb:

  • That does not allow a vehicle to use that visual intersection?

  • Is the application for pedestrians and therefore the pedestrian can easily walk on the small curb?

  • Is the application for the electricity and the electrical lines than can easily be extended on top of the small curb?

• Is there a big cliff and from eagles view look like the dead end is close to the segment?

When there are many dead ends, to speed up, the Contraction - Familia de funciones functions can be used to divide the problem.

Linear edges

To get the linear edges:

SELECT id FROM vertices
WHERE array_length(in_edges || out_edges, 1) = 2;
 id
----
  3
 15
 17
(3 rows)

This information is correct, for example, when the application is taking into account speed bumps, stop signals.

When there are many linear edges, to speed up, the Contraction - Familia de funciones functions can be used to divide the problem.

Function’s structure

Once the graph preparation work has been done above, it is time to use a

La forma general de una llamada a una función de pgRouting es:

pgr_<name>(Inner queries, parameters, [ Optional parameters)

Donde:

• Inner queries: Are compulsory parameters that are TEXT strings containing SQL queries.

• parameters: Additional compulsory parameters needed by the function.

• Optional parameters: Are non compulsory named parameters that have a default value when omitted.

The compulsory parameters are positional parameters, the optional parameters are named parameters.

For example, for this pgr_dijkstra signature:

pgr_dijkstra(SQL de aristas, salida, destino, [directed])

• SQL de aristas:

  • Is the first parameter.

  • It is compulsory.

  • It is an inner query.

  • It has no name, so Edges SQL gives an idea of what kind of inner query needs to be used

• vid inical:

  • Is the second parameter.

  • It is compulsory.

  • It has no name, so start vid gives an idea of what the second parameter’s value should contain.

• destino

  • Is the third parameter.

  • It is compulsory.

  • It has no name, so end vid gives an idea of what the third parameter’s value should contain

• directed

  • Is the fourth parameter.

  • It is optional.

  • It has a name.

The full description of the parameters are found on the Parameters section of each function.

Function’s overloads

A function might have different overloads. The most common are called:

• Uno a Uno

• Uno a Muchos

• Muchos a Uno

• Muchos a Muchos

• Combinaciones

Dependiendo de la sobrecarga, los tipos de los parámetros cambian.

• One: ANY-INTEGER

• Many: ARRAY [ANY-INTEGER]

Depending of the function the overloads may vary. But the concept of parameter type change remains the same.

Uno a Uno

Cuando se rutea desde:

• Desde un vértice inicial

• al un vértice final

Uno a Muchos

Cuando se rutea desde:

• Desde un vértice inicial

• a los vértices finales many

Muchos a Uno

Cuando se rutea desde:

• Desde muchos vértices iniciales

• al un vértice final

Muchos a Muchos

Cuando se rutea desde:

• Desde muchos vértices iniciales

• a los vértices finales many

Combinaciones

Cuando se rutea desde:

• A partir de muchos diferentes vértices de inicio

• a muchos diferentes vértices finales

• Cada tupla especifica un par de vértices iniciales y un vértice final

• Los usuarios pueden definir las combinaciones como deseen.

• Necesita una SQL de combinaciones

Consultas Internas

Hay varios tipos de consultas internas válidas y también las columnas devueltas dependen de la función. El tipo de consulta interna dependerá de los requisitos de las funcion(es). Para simplificar la variedad de tipos, se utiliza ENTEROS y FLOTANTES.

Donde:

ENTEROS:

SMALLINT, INTEGER, BIGINT

FLOTANTES:

SMALLINT, INTEGER, BIGINT, REAL, FLOAT

SQL aristas

General

SQL de aristas para

• Dijkstra - Familia de funciones

• withPoints - Familia de funciones

• Bidirectional Dijkstra - Familia de funciones

• Componentes - Familia de funciones

• Kruskal - Familia de funciones

• Prim - Familia de funciones

• Some uncategorised functions

Columna	Tipo	x Defecto	Descripción
id	ENTEROS		Identificador de la arista.
source	ENTEROS		Identificador del primer vértice de la arista.
target	ENTEROS		Identificador del segundo vértice de la arista.
cost	FLOTANTES		Peso de la arista (source, target)
reverse_cost	FLOTANTES	-1	Peso de la arista (target, source) Cuando negativo: la arista (target, source) no existe, por lo tanto no es parte del grafo.

Donde:

ENTEROS:

SMALLINT, INTEGER, BIGINT

FLOTANTES:

SMALLINT, INTEGER, BIGINT, REAL, FLOAT

General without id

SQL de aristas para

• Todos los Pares - Familia de Funciones

Columna	Tipo	x Defecto	Descripción
source	ENTEROS		Identificador del primer vértice de la arista.
target	ENTEROS		Identificador del segundo vértice de la arista.
cost	FLOTANTES		Peso de la arista (source, target)
reverse_cost	FLOTANTES	-1	Peso de la arista (target, source) Cuando negativo: la arista (target, source) no existe, por lo tanto no es parte del grafo.

Donde:

ENTEROS:

SMALLINT, INTEGER, BIGINT

FLOTANTES:

SMALLINT, INTEGER, BIGINT, REAL, FLOAT

General with (X,Y)

SQL de aristas para

• A* - Familia de Funciones

• A* Bidireccional - Familia de Funciones

Parámetro	Tipo	x Defecto	Descripción
id	ENTEROS		Identificador de la arista.
source	ENTEROS		Identificador del primer vértice de la arista.
target	ENTEROS		Identificador del segundo vértice de la arista.
cost	FLOTANTES		Peso de la arista (source, target) Cuando es negativo: la arista (source, target) no existe, por lo tanto no es parte del grafo.
reverse_cost	FLOTANTES	-1	Peso de la arista (target, source), Cuando negativo: la arista (target, source) no existe, por lo tanto no es parte del grafo.
x1	FLOTANTES		Coordenada X del vértice source.
y1	FLOTANTES		Coordenada Y del vértice source.
x2	FLOTANTES		Coordenada X del vértice target.
y2	FLOTANTES		Coordenada Y del vértice target.

Donde:

ENTEROS:

SMALLINT, INTEGER, BIGINT

FLOTANTES:

SMALLINT, INTEGER, BIGINT, REAL, FLOAT

Flujo

Edges SQL for Flow - Familia de funciones

SQL de aristas para

• pgr_pushRelabel

• pgr_edmondsKarp

• pgr_boykovKolmogorov

Columna	Tipo	x Defecto	Descripción
id	ENTEROS		Identificador de la arista.
source	ENTEROS		Identificador del primer vértice de la arista.
target	ENTEROS		Identificador del segundo vértice de la arista.
capacity	ENTEROS		Peso de la arista (source, target)
reverse_capacity	ENTEROS	-1	Peso de la arista (target, source) Cuando negativo: la arista (target, source) no existe, por lo tanto no es parte del grafo.

Donde:

ENTEROS:

SMALLINT, INTEGER, BIGINT

FLOTANTES:

SMALLINT, INTEGER, BIGINT, REAL, FLOAT

Edges SQL for the following functions of Flow - Familia de funciones

• pgr_maxFlowMinCost - Experimental

• pgr_maxFlowMinCost_Cost - Experimental

Columna	Tipo	x Defecto	Descripción
id	ENTEROS		Identificador de la arista.
source	ENTEROS		Identificador del primer vértice de la arista.
target	ENTEROS		Identificador del segundo vértice de la arista.
capacity	ENTEROS		Capacidad de la arista (source, target) Cuando negativo: la arista (target, source) no existe, por lo tanto no es parte del grafo.
reverse_capacity	ENTEROS	-1	Capacidad de la arista (target, source) Cuando negativo: la arista (target, source) no existe, por lo tanto no es parte del grafo.
cost	FLOTANTES		Peso de la arista (source, target) si existe
reverse_cost	FLOTANTES	\(-1\)	Peso de la arista (target, source) si existe

Donde:

ENTEROS:

SMALLINT, INTEGER, BIGINT

FLOTANTES:

SMALLINT, INTEGER, BIGINT, REAL, FLOAT

SQL Combinaciones

Used on combination signatures

Parámetro	Tipo	Descripción
source	ENTEROS	Identificador del vértice de salida.
target	ENTEROS	Identificador del vértice de llegada.

Donde:

ENTEROS:

SMALLINT, INTEGER, BIGINT

SQL restricciones

Columna	Tipo	Descripción
path	ARRAY [ENTEROS]	Secuencia de identificadores de aristas que forman un camino que no se permite tomar. - Arreglos vacios o NULL son ignorados. - Arreglos que tienen NULL arrojan una excepción.
Cost	FLOTANTES	Costo de tomar el camino prohibido.

Donde:

ENTEROS:

SMALLINT, INTEGER, BIGINT

FLOTANTES:

SMALLINT, INTEGER, BIGINT, REAL, FLOAT

SQL de puntos

SQL de puntos para

• withPoints - Familia de funciones

Parámetro	Tipo	x Defecto	Descripción
pid	ENTEROS	valor	Identificador del punto. Use con un valor positivo, dado que internamente se convertirá a un valor negativo Si columna esta presente, no puede ser NULL. Si columna no esta presente, un valor secuencial negativo se otorgará automáticamente.
edge_id	ENTEROS		Identificador de la arista «más cercana» al punto.
fraction	FLOTANTES		El valor en <0,1> que indica la posición relativa desde el primer punto de la arista.
side	CHAR	b	Valor en [b, r, l, NULL] que indica si el punto es: A la derecha r, A la izquierda l, En ambos lados b, NULL

Donde:

ENTEROS:

SMALLINT, INTEGER, BIGINT

FLOTANTES:

SMALLINT, INTEGER, BIGINT, REAL, FLOAT

Parámetros

The main parameter of the majority of the pgRouting functions is a query that selects the edges of the graph.

Parámetro	Tipo	Descripción
SQL de aristas	TEXT	SQL de aristas descritas más adelante.

Depending on the family or category of a function it will have additional parameters, some of them are compulsory and some are optional.

The compulsory parameters are nameless and must be given in the required order. The optional parameters are named parameters and will have a default value.

Párametros para las funciones Via

• pgr_dijkstraVia - Proposed

Parámetro	Tipo	x Defecto	Descripción
SQL de aristas	TEXT		Consulta SQL como se describe.
vértices	ARRAY [ENTEROS]		Arreglo ordenado de identificadores de vértices que serán visitados.
directed	BOOLEAN	true	Cuando true el gráfo se considera Dirigido Cuando false el gráfico se considera como No Dirigido.
strict	BOOLEAN	false	Cuando true si un camino le faltan paradas y regresa EMPTY SET Cuando false, ignora las rutas faltantes y devuelve todas las rutas encontradas
U_turn_on_edge	BOOLEAN	true	Cuando true saliendo de un vértice visitado no intentará evitar el uso de la arista utilizada para alcanzarlo. En otras palabras, se permite la vuelta en U usando la arista con el mismo identificador. Cuando false al salir de un vértice visitado intenta evitar el uso de la arista utilizada para alcanzarlo. En otras palabras, se utiliza la vuelta en U utilizando la arista con el mismo identificador cuando no se encuentra ninguna otra ruta.

Para las funciones de TRSP

• pgr_trsp - Turn Restriction Shortest Path (TRSP)

Columna	Tipo	Descripción
SQL de aristas	TEXT	Consulta SQL como se describe.
SQL de restricciones	TEXT	Consulta SQL como se describe.
SQL de combinaciones	TEXT	SQL de combinaciones como se describe a abajo
salida	ENTEROS	Identificador del vértice de salida.
salidas	ARRAY [ENTEROS]	Arreglo de identificadores de vértices destino.
destino	ENTEROS	Identificador del vértice de salida.
destinos	ARRAY [ENTEROS]	Arreglo de identificadores de vértices destino.

Donde:

ENTEROS:

SMALLINT, INTEGER, BIGINT

Columnas de Resultados

Hay varios tipos de columnas devueltas que dependen de la función.

Columnas devueltas para una trayectoria

Used on functions that return one path solution

Devuelve el conjunto de (seq, path_seq [, start_vid] [, end_vid], node, edge, cost, agg_cost)

Columna	Tipo	Descripción
seq	INTEGER	Valor secuencial a partir de 1.
path_seq	INTEGER	Posición relativa en la ruta. Tiene el valor 1 para el inicio de una ruta.
start_vid	BIGINT	Identificador del vértice inicial. Se devuelve cuando hay varias vetrices iniciales en la consulta. Muchos a Uno Muchos a Muchos
end_vid	BIGINT	Identificador del vértice final. Se devuelve cuando hay varios vértices finales en la consulta. Uno a Muchos Muchos a Muchos
node	BIGINT	Identificador del nodo en la ruta de start_vid a end_vid.
edge	BIGINT	Identificador de la arista utilizado para ir del node al siguiente nodo de la secuencia de ruta. -1 para el último nodo de la ruta.
cost	FLOAT	Costo para atravesar desde node usando edge hasta el siguiente nodo en la secuencia de la ruta.
agg_cost	FLOAT	Costo agregado desde start_vid hasta node.

Used on functions the following:

• pgr_withPoints - Propuesto

Devuelve el conjunto de (seq, path_seq [, start_pid] [, end_pid], node, edge, cost, agg_cost)

Columna	Tipo	Descripción
seq	INTEGER	Valor secuencial a partir de 1.
path_seq	INTEGER	Posición relativa en la ruta. 1 para la primera fila de la secuencia de ruta.
start_pid	BIGINT	Identificador del vértice/punto inicial de la ruta. Cunado positivo, es el identificador del vértice inicial. Cuando negativo, es el identificador del punto inicial. Regresado en Muchos a Uno y Muchos a Muchos
end_pid	BIGINT	Identificador d vértice/punto final del camino. Cuando negativo, es el identificador del vertice final. Cuando es negativo, es el identificador del vértice destino. Regresado en Uno a Muchos y Muchos a Muchos
node	BIGINT	Identificador del nodo en la ruta de start_vid a end_vid. Cuando es positivo, es el identificador de un vértice. Cuando es negativo, es identificador de un punto.
edge	BIGINT	Identificador de la arsita utilizada para ir del node al siguiente nodo de la secuencia de ruta. -1 para la última fila de la ruta.
cost	FLOAT	Costo para atravesar desde node usando edge hasta el siguiente nodo en la secuencia de la ruta. 0 para la primera fila de la secuencia de ruta.
agg_cost	FLOAT	Costo agregado desde start_vid hasta node. 0 para la primera fila de la secuencia de ruta.

Used on functions the following:

• pgr_dijkstraNear - Propuesto

Regresa (seq, path_seq, start_vid, end_vid, node, edge, cost, agg_cost)

Columna	Tipo	Descripción
seq	INTEGER	Valor secuencial a partir de 1.
path_seq	INTEGER	Posición relativa en la ruta. Tiene el valor 1 para el inicio de una ruta.
start_vid	BIGINT	Identificador del vértice inicial de la ruta actual.
end_vid	BIGINT	Identificador del vértice final de la ruta actual.
node	BIGINT	Identificador del nodo en la ruta de start_vid a end_vid.
edge	BIGINT	Identificador de la arista utilizado para ir del node al siguiente nodo de la secuencia de ruta. -1 para el último nodo de la ruta.
cost	FLOAT	Costo para atravesar desde node usando edge hasta el siguiente nodo en la secuencia de la ruta.
agg_cost	FLOAT	Costo agregado desde start_vid hasta node.

Multiple paths

Selective for multiple paths.

The columns depend on the function call.

Conjunto de (seq, path_id, path_seq [, start_vid] [, end_vid], node, edge, cost, agg_cost)

Columna	Tipo	Descripción
seq	INTEGER	Valor secuencial a partir de 1.
path_id	INTEGER	Identificador del camino. Tiene valor 1 para el primero de la ruta de start_vid a end_vid.
path_seq	INTEGER	Posición relativa en la ruta. Tiene el valor 1 para el inicio de una ruta.
start_vid	BIGINT	Identificador del vértice inicial. Se devuelve cuando hay varias vetrices iniciales en la consulta. Muchos a Uno Muchos a Muchos Combinaciones
end_vid	BIGINT	Identificador del vértice final. Se devuelve cuando hay varios vértices finales en la consulta. Uno a Muchos Muchos a Muchos Combinaciones
node	BIGINT	Identificador del nodo en la ruta de start_vid a end_vid.
edge	BIGINT	Identificador de la arista utilizado para ir del node al siguiente nodo de la secuencia de ruta. -1 para el último nodo de la ruta.
cost	FLOAT	Costo para atravesar desde node usando edge hasta el siguiente nodo en la secuencia de la ruta.
agg_cost	FLOAT	Costo agregado desde start_vid hasta node.

Non selective for multiple paths

Regardless of the call, al the columns are returned.

• pgr_trsp - Turn Restriction Shortest Path (TRSP)

Devuelve el conjunto de (seq, path_id, path_seq, start_vid, end_vid, node, edge, cost, agg_cost)

Columna	Tipo	Descripción
seq	INTEGER	Valor secuencial a partir de 1.
path_id	INTEGER	Identificador del camino. Tiene valor 1 para el primero de la ruta de start_vid a end_vid.
path_seq	INTEGER	Posición relativa en la ruta. Tiene el valor 1 para el inicio de una ruta.
start_vid	BIGINT	Identificador del vértice de salida.
end_vid	BIGINT	Identificador del vértice destino.
node	BIGINT	Identificador del nodo en la ruta de start_vid a end_vid.
edge	BIGINT	Identificador de la arista utilizado para ir del node al siguiente nodo de la secuencia de ruta. -1 para el último nodo de la ruta.
cost	FLOAT	Costo para atravesar desde node usando edge hasta el siguiente nodo en la secuencia de la ruta.
agg_cost	FLOAT	Costo agregado desde start_vid hasta node.

Columnas devueltas para funciones de costo

Used in the following

• Costo - Categoría

• Cost Matrix - Categoría

• Todos los Pares - Familia de Funciones

Conjunto de (start_vid, end_vid, agg_cost)

Columna	Tipo	Descripción
start_vid	BIGINT	Identificador del vértice de salida.
end_vid	BIGINT	Identificador del vértice destino.
agg_cost	FLOAT	Costo afregado desde start_vid hasta end_vid.

Nota

Cuando las columnas del vértice inicial o del destino continen valores negativos, el identificador es para un Punto.

Columnas devueltas para funciones de flujo

Edges SQL for the following

• Flow - Familia de funciones

Columna	Tipo	Descripción
seq	INT	Valor secuencial a partir de 1.
arista	BIGINT	Identificador de la arista en la consulta original(edges_sql).
start_vid	BIGINT	Identificador del primer vértice de la arista.
end_vid	BIGINT	Identificador del segundo vértice de la arista.
flujo	BIGINT	Flujo a través del arista en la dirección (start_vid, end_vid).
residual_capacity	BIGINT	Capacidad residual del arista en la dirección (start_vid, end_vid).

Edges SQL for the following functions of Flow - Familia de funciones

• pgr_maxFlowMinCost - Experimental

Columna	Tipo	Descripción
seq	INT	Valor secuencial a partir de 1.
arista	BIGINT	Identificador de la arista en la consulta original(edges_sql).
origen	BIGINT	Identificador del primer vértice de la arista.
objetivo	BIGINT	Identificador del segundo vértice de la arista.
flujo	BIGINT	Flujo a través de la arista en la dirección (origen, destino).
residual_capacity	BIGINT	Capacidad residual de la arista en la dirección (origen, destino).
costo	FLOAT	El costo de enviar este flujo a través de la arista en la dirección (origen, destino).
agg_cost	FLOAT	El costo agregado.

Return columns for spanning tree functions

Edges SQL for the following

• pgr_prim

• pgr_kruskal

Devuelve CONJUNTO DE (edge, cost)

Columna	Tipo	Descripción
edge	BIGINT	Identificador de la arista.
cost	FLOAT	Coste para atravezar el borde.

Consejos de Rendimiento

Para las funciones de Ruteo

Para obtener resultados más rápidos, delimitar las consultas a un área de interés para el ruteo.

En este ejemplo, usar una consulta SQL interna que no incluya algunas aristas en la función de ruteo y dentro del área de los resultados.

SELECT * FROM pgr_dijkstra($$
  SELECT id, source, target, cost, reverse_cost from edges
  WHERE geom && (SELECT st_buffer(geom, 1) AS myarea
    FROM edges WHERE id = 2)$$,
  1, 2);
 seq | path_seq | node | edge | cost | agg_cost
-----+----------+------+------+------+----------
(0 rows)

Cómo contribuir

Wiki

• Edita una página existente Wiki de pgRouting.

• O crea una nueva página Wiki

  • Crear una página en el Wiki de pgRouting

  • Asigne al título un nombre apropiado

• Ejemplo

Agregar funcionalidad a pgRouting

Consultar la documentation de desarrolladores

Índices y tablas

• Índice

• Página de Búsqueda