Versiones no soportadas:2.6 2.5 2.4 2.3 2.2 2.1 2.0
Conceptos de pgRouting¶
Esta es una guía simple que va a través de los pasos básicos para empezar trabajar con pgRouting. Esta guía cubre:
Grafos¶
Definición de grafo¶
Un grafo es un par ordenado
Hay diferentes tipos de grafos:
Grafo no dirigido
Grafo no dirigido simple
Grafo dirigido
Grafo dirigido simple
Grafos:
No tienen geometrías.
Algunos problemas de teoría de grafos requieren tener pesos, llamados cost en pgRouting.
En pgRouting hay varias maneras de representar in grafo en la base de datos:
Con
cost(
id,source,target,cost)
Con
costyreverse_cost(
id,source,target,cost,reverse_cost)
Donde:
Columna |
Descripción |
|---|---|
|
Identificador de la asirsta. Requerimiento para mantener consistente la base de datos. |
|
Identificador de un vértice. |
|
Identificador de un vértice. |
|
Peso de la arista (
|
|
Peso de la arista (
|
La decisión del grafo de ser directed o undirected es resultado al ejecutar el algoritmo de pgRouting.
Grafo con cost¶
El grafo ponderado dirigido,
Datos de l grafo se obtienen mediante una consulta
SELECT id, source, target, cost FROM edgesEl conjunto de aristas
Aristas donde
costes no negativo son parte del grafo.
el conjunto de vértices
Todos los vértices``source`` y
targetson parte del grafo.
Grafo dirigido
En un grafo dirigido la arista
Para los siguientes datos:
SELECT *
FROM (VALUES (1, 1, 2, 5), (2, 1, 3, -3))
AS t(id, source, target, cost);
id | source | target | cost
----+--------+--------+------
1 | 1 | 2 | 5
2 | 1 | 3 | -3
(2 rows)
La arista
Los datos se representan en el siguiente grafo:
![digraph G {
1 -> 2 [label="1(5)"];
3;
}](_images/graphviz-6a22e17e4c49cbe911a2c3c04aea2e93942005ce.png)
Grafo no dirigido
En un grafo no dirigido la arista
En términos de un grafo dirigido es como tener dos aristas:
Para los siguientes datos:
SELECT *
FROM (VALUES (1, 1, 2, 5), (2, 1, 3, -3))
AS t(id, source, target, cost);
id | source | target | cost
----+--------+--------+------
1 | 1 | 2 | 5
2 | 1 | 3 | -3
(2 rows)
Arista
Los datos se representan en el siguiente grafo:
![graph G {
1 -- 2 [label="1(5)"];
3;
}](_images/graphviz-a9ff7d505ee3aa8158a1f3439d4325a71f0dbcae.png)
Grafo con cost y reverse_cost¶
El ponderado del grafo dirigido,
Datos de l grafo se obtienen mediante una consulta
SELECT id, source, target, cost, reverse_cost FROM edgesEl conjunto de aristas
Aristas
costes no negativo son parte del grafo.Aristas
reverse_costes no negativo son parte del grafo.
El conjunto de vértices
Todos los vértices``source`` y
targetson parte del grafo.
Grafo dirigido
En un grafo dirigido ambas aristas tiene direccionalidad
arista
arista
Para los siguientes datos:
SELECT *
FROM (VALUES (1, 1, 2, 5, 2), (2, 1, 3, -3, 4), (3, 2, 3, 7, -1))
AS t(id, source, target, cost, reverse_cost);
id | source | target | cost | reverse_cost
----+--------+--------+------+--------------
1 | 1 | 2 | 5 | 2
2 | 1 | 3 | -3 | 4
3 | 2 | 3 | 7 | -1
(3 rows)
Aristas no son parte del grafo:
Los datos se representan en el siguiente grafo:
![digraph G {
1 -> 2 [label="1(5)"];
2 -> 1 [label="1(2)"];
3 -> 1 [label="2(4)"];
2 -> 3 [label="3(7)"];
}](_images/graphviz-cf2723f26bd1c3ee60f314423c76e21eb5708d4e.png)
Grafo no dirigido
En un grafo dirigido ambas aristas no tiene direccionalidad
Arista
Arista
En términos de un grafo dirigido es como tener cuatro aristas:
Para los siguientes datos:
SELECT *
FROM (VALUES (1, 1, 2, 5, 2), (2, 1, 3, -3, 4), (3, 2, 3, 7, -1))
AS t(id, source, target, cost, reverse_cost);
id | source | target | cost | reverse_cost
----+--------+--------+------+--------------
1 | 1 | 2 | 5 | 2
2 | 1 | 3 | -3 | 4
3 | 2 | 3 | 7 | -1
(3 rows)
Aristas no son parte del grafo:
Los datos se representan en el siguiente grafo:
![graph G {
1 -- 2 [label="1(5)"];
2 -- 1 [label="1(2)"];
3 -- 1 [label="2(4)"];
2 -- 3 [label="3(7)"];
}](_images/graphviz-7cf300b7d69445756b30b2135af90e936a5dd9e4.png)
Grafos sin geometrías¶
Relaciones personales, genealogía, problemas de dependencia de archivos puede ser resueltos usando pgRouting. Esos problemas, normalmente, no vienen con las geometrías asociadas con el grafo.
Ejemplo de Wiki¶
Resuelva el problema de ejemplo tomado de wikipedia):
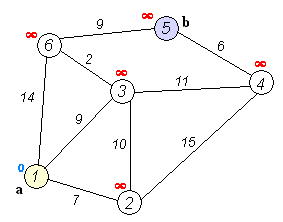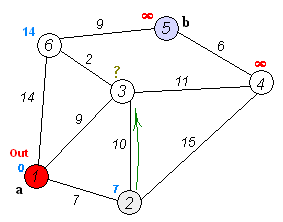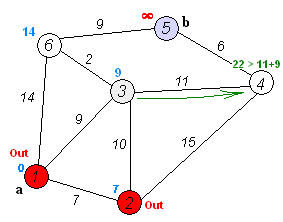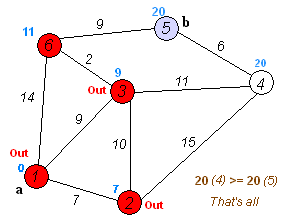
Donde:
Problema es encontrar el camino mas corto desde
Es un grafo dirigido.
Aunque visualmente se vea con geometrías, el dibujo no es a escala.
Las geometrías no esta asociadas con los vértices o aristas
Tiene 6 vértices
Tiene 9 aristas:
El grafo puede ser representados de varias maneras por ejemplo:
![graph G {
rankdir="LR";
1 [color="red"];
5 [color="green"];
1 -- 2 [label="(7)"];
5 -- 6 [label="(9)"];
1 -- 3 [label="(9)"];
1 -- 6 [label="(14)"];
2 -- 3 [label="(10)"];
2 -- 4 [label="(13)"];
3 -- 4 [label="(11)"];
3 -- 6 [label="(2)"];
4 -- 5 [label="(6)"];
}](_images/graphviz-aa83b370a30d7a5c2be123929174e31044bca152.png)
Prepara la base de datos¶
Crea una base de datos para el ejemplo, acceda a la base de datos e instala pgRouting:
$ createdb wiki
$ psql wiki
wiki =# CREATE EXTENSION pgRouting CASCADE;
Crear una tabla¶
Los elementos básicos necesarios para realizar routing básico en un grafo no dirigido son:
Columna |
Tipo |
Descripción |
|---|---|---|
|
ENTEROS |
Identificador de la arista. |
|
ENTEROS |
Identificador del primer vértice de la arista. |
|
ENTEROS |
Identificador del segundo vértice de la arista. |
|
FLOTANTES |
Peso de la arista ( |
Donde:
- ENTEROS:
SMALLINT, INTEGER, BIGINT- FLOTANTES:
SMALLINT, INTEGER, BIGINT, REAL, FLOAT
Usando este diseño de tabla para este ejemplo:
CREATE TABLE wiki (
id SERIAL,
source INTEGER,
target INTEGER,
cost INTEGER);
CREATE TABLE
Introduzca los datos¶
INSERT INTO wiki (source, target, cost) VALUES
(1, 2, 7), (1, 3, 9), (1, 6, 14),
(2, 3, 10), (2, 4, 15),
(3, 6, 2), (3, 4, 11),
(4, 5, 6),
(5, 6, 9);
INSERT 0 9
En cuentre el camino más corto¶
Para resolver el ejemplo se usa pgr_dijkstra:
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost FROM wiki',
1, 5, false);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 1 | 5 | 1 | 2 | 9 | 0
2 | 2 | 1 | 5 | 3 | 6 | 2 | 9
3 | 3 | 1 | 5 | 6 | 9 | 9 | 11
4 | 4 | 1 | 5 | 5 | -1 | 0 | 20
(4 rows)
Para ir de
![graph G {
rankdir="LR";
1 [color="red"];
5 [color="green"];
1 -- 2 [label="(7)"];
5 -- 6 [label="(9)", color="blue"];
1 -- 3 [label="(9)", color="blue"];
1 -- 6 [label="(14)"];
2 -- 3 [label="(10)"];
2 -- 4 [label="(13)"];
3 -- 4 [label="(11)"];
3 -- 6 [label="(2)", color="blue"];
4 -- 5 [label="(6)"];
}](_images/graphviz-2be84fbb8166d4e067f5592a16b83c30776ea85c.png)
Información de vertices¶
Para obtener la información de los vértices, use pgr_extractVertices
SELECT id, in_edges, out_edges
FROM pgr_extractVertices('SELECT id, source, target FROM wiki');
id | in_edges | out_edges
----+----------+-----------
3 | {2,4} | {6,7}
5 | {8} | {9}
4 | {5,7} | {8}
2 | {1} | {4,5}
1 | | {1,2,3}
6 | {3,6,9} |
(6 rows)
Grafos con geometrías¶
Crear una Base de Datos de Ruteo¶
El primer paso para crear una base de datos y cargar pgRouting en la base de datos.
Típicamente se crea una base de datos para cada proyecto.
Una vez que se tenga una base de datos, cargue sus datos y construya la aplicación de routeo en esa base de datos.
createdb sampledata
psql sampledata -c "CREATE EXTENSION pgrouting CASCADE"
Cargar Datos¶
Hay varias maneras de cargar tus datos en pgRouting.
Creando manualmente la base de datos.
Datos Muestra: un pequeño grafo utilizado en los ejemplos de la documentación
Usando osm2pgrouting
Existen varias herramientas de codigo abierto que pueden ayudar, como:
- shp2pgsql:
cargador a postgresql de archivos shape
- ogr2ogr:
herramienta de conversión de datos vectoriales
- osm2pgsql:
cargar datos de OSM a postgresql
Tener en cuenta que estas herramientas no importan los datos a una estructura compatible con pgRouting y cuando esto sucede, la topología necesita ser ajustada.
Rompe en segmentos cada intersección segmento-segmento
Cuando falte, agregue columnas y asigne valores a
source,target,cost,reverse_cost.Conecte un grafo desconectado.
Crea la topología de un grafo completo
Crea uno o mas grafos según la aplicación que se desarrolla.
Crea un grafo contraído para calles de alta velocidad
Crear grafos por estado/país
En pocas palabras:
Prepara el grafo
Qué y cómo preparar el grafo, dependerá de la aplicación y/o de la calidad de los datos y/o de lo cerca que esté la información de tener una topología utilizable por pgRouting y/o algunos otros factores no mencionados.
Los pasos para preparar el grafo implican operaciones de geometría utilizando PostGIS y algunos otros implican operaciones de grafos como pgr_contraction para contraer un grafo.
El taller tiene un paso a paso sobre cómo preparar un grafo utilizando datos de Open Street Map, para una pequeña aplicación.
El uso de índices en el diseño de bases de datos en general:
Tener las geometrías indexadas.
Tener indexadas las columnas de identificadores.
Consultar la documentación de PostgreSQL y la documentación de PostGIS.
Construir una topología de ruteo¶
La información básica para usar la mayoría de las funciones de pgRouting id, source, target, cost, [reverse_cost] es lo que en pgRouting se llama topología de ruteo.
reverse_cost es opcional pero se recomienda encarecidamente tenerlo para reducir el tamaño de la base de datos debido al tamaño de las columnas de geometría. Dicho esto, en esta documentación se utiliza reverse_cost.
Cuando los datos vienen con geometrías y no hay topología de ruteo, entonces este paso es necesario.
Todos los vértices iniciales y finales de las geometrías necesitan un identificador que se almacenará en las columnas source y target de la tabla de los datos. Del mismo modo, cost y reverse_cost necesitan tener el valor de atravesar la arista en ambas direcciones.
Si las columnas no existen, hay que añadirlas a la tabla en cuestión. (véase ALTER TABLE)
La función pgr_extractVertices se utiliza para crear una tabla de vértices basada en el identificador de arista y la geometría de la arista del grafo.
SELECT * INTO vertices
FROM pgr_extractVertices('SELECT id, geom FROM edges ORDER BY id');
SELECT 18
Finalmente, utilizando los datos almacenados en las tablas de vértices, se rellenan los campos source y target.
/* -- set the source information */
UPDATE edges AS e
SET source = v.id, x1 = x, y1 = y
FROM vertices AS v
WHERE ST_StartPoint(e.geom) = v.geom;
UPDATE 24
/* -- set the target information */
UPDATE edges AS e
SET target = v.id, x2 = x, y2 = y
FROM vertices AS v
WHERE ST_EndPoint(e.geom) = v.geom;
UPDATE 24
Los datos procedentes de OSM y utilizando osm2pgrouting <https://github.com/pgRouting/osm2pgrouting>`__ como herramienta de importación, vienen con la topología de ruteo. Ver un ejemplo de uso de ``osm2pgrouting en el workshop.
Ajustar los costes¶
Para este ejemplo los valores coste y coste_inverso van a ser el doble de la longitud de la geometría.
Actualizar los costes a la longitud de la geometría¶
Suponer que las columnas cost y reverse_cost de los datos de la muestra representan:
Utilizando esa información de actualización a la longitud de las geometrías:
UPDATE edges SET
cost = sign(cost) * ST_length(geom) * 2,
reverse_cost = sign(reverse_cost) * ST_length(geom) * 2;
UPDATE 18
Lo que da los siguientes resultados:
SELECT id, cost, reverse_cost FROM edges;
id | cost | reverse_cost
----+--------------------+--------------------
6 | 2 | 2
7 | 2 | 2
4 | 2 | 2
5 | 2 | -2
8 | 2 | 2
12 | 2 | -2
11 | 2 | -2
10 | 2 | 2
17 | 2.999999999998 | 2.999999999998
14 | 2 | 2
18 | 3.4000000000000004 | 3.4000000000000004
13 | 2 | -2
15 | 2 | 2
16 | 2 | 2
9 | 2 | 2
3 | -2 | 2
1 | 2 | 2
2 | -2 | 2
(18 rows)
Tener en cuenta que para poder seguir los ejemplos de la documentación, todo se basa en el grafo original.
Volviendo a los datos originales:
UPDATE edges SET
cost = sign(cost),
reverse_cost = sign(reverse_cost);
UPDATE 18
Actualizar los costes en función de los códigos¶
Otros conjuntos de datos, pueden tener una columna con valores como
FTflujo de vehículos en la dirección de la geometríaTFflujo del vehículo opuesto a la dirección de la geometríaBflujo de vehículos en ambas direcciones
Preparar una columna de códigos para el ejemplo:
ALTER TABLE edges ADD COLUMN direction TEXT;
ALTER TABLE
UPDATE edges SET
direction = CASE WHEN (cost>0 AND reverse_cost>0) THEN 'B' /* both ways */
WHEN (cost>0 AND reverse_cost<0) THEN 'FT' /* direction of the LINESSTRING */
WHEN (cost<0 AND reverse_cost>0) THEN 'TF' /* reverse direction of the LINESTRING */
ELSE '' END;
UPDATE 18
/* unknown */
Ajuste de los costes en función de los códigos:
UPDATE edges SET
cost = CASE WHEN (direction = 'B' OR direction = 'FT')
THEN ST_length(geom) * 2
ELSE -1 END,
reverse_cost = CASE WHEN (direction = 'B' OR direction = 'TF')
THEN ST_length(geom) * 2
ELSE -1 END;
UPDATE 18
Lo que da los siguientes resultados:
SELECT id, cost, reverse_cost FROM edges;
id | cost | reverse_cost
----+--------------------+--------------------
6 | 2 | 2
7 | 2 | 2
4 | 2 | 2
5 | 2 | -1
8 | 2 | 2
12 | 2 | -1
11 | 2 | -1
10 | 2 | 2
17 | 2.999999999998 | 2.999999999998
14 | 2 | 2
18 | 3.4000000000000004 | 3.4000000000000004
13 | 2 | -1
15 | 2 | 2
16 | 2 | 2
9 | 2 | 2
3 | -1 | 2
1 | 2 | 2
2 | -1 | 2
(18 rows)
Volviendo a los datos originales:
UPDATE edges SET
cost = sign(cost),
reverse_cost = sign(reverse_cost);
UPDATE 18
ALTER TABLE edges DROP COLUMN direction;
ALTER TABLE
Compruebe la Topología de Ruteo¶
Hay muchos problemas posibles en un grafo.
Es posible que los datos utilizados no se hayan diseñado teniendo en cuenta el ruteo.
Un grafo tiene unos requisitos muy específicos.
El grafo está desconectado.
Hay intersecciones no deseadas.
El grafo es demasiado grande y hay que contraerlo.
Se necesita un subgrafo para la aplicación.
y muchos otros problemas que el usuario de pgRouting, es decir, el desarrollador de aplicaciones, puede encontrar.
Aristas que se cruzan¶
Para obtener las aristas que se cruzan:
SELECT a.id, b.id
FROM edges AS a, edges AS b
WHERE a.id < b.id AND st_crosses(a.geom, b.geom);
id | id
----+----
13 | 18
(1 row)
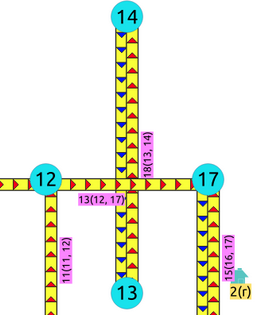
Esa información es correcta, por ejemplo, cuando en términos de vehículos, es un túnel o puente cruczando sobre otra carretera.
Puede ser incorrecto, por ejemplo:
Cuando en realidad es una intersección de carreteras, donde los vehículos pueden hacer giros.
En cuanto a las líneas eléctricas, son capaces de cambiar de carretera incluso en un túnel o puente.
Cuando es incorrecta, hay que arreglarla:
Para vehículos y peatones
Si los datos provienen de OSM y fueron importados a la base de datos utilizando
osm2pgrouting, la corrección debe hacerse en el OSM portal y los datos ser importados de nuevo.En general, cuando los datos proceden de un proveedor que tiene los datos preparados para el ruteo de vehículos, y hay un problema, los datos deben ser fijados por el proveedor
Para aplicaciones muy específicas
Los datos son correctos desde el punto de vista de la circulación de vehículos o peatones.
Los datos necesitan un arreglo local para la aplicación específica.
Una vez analizados uno a uno los cruces, para los que necesitan un arreglo local, hay que dividir las aristas.
Hay que añadir las nuevas aristas a la tabla de aristas, actualizar el resto de atributos en las nuevas aristas, eliminar las aristas antiguas y actualizar la topología de encaminamiento.
Arreglando una intersección¶
In this example the original edge table will be used to store the additional geometries.
An example use without results
Routing from
SELECT *
FROM pgr_dijkstra('SELECT id, source, target, cost, reverse_cost FROM edges', 1, 18);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
(0 rows)
Analyze the network for intersections.
SELECT
e1.id id1, e2.id id2,
ST_AsText(ST_Intersection(e1.geom, e2.geom)) AS point
FROM edges e1, edges e2
WHERE e1.id < e2.id AND ST_Crosses(e1.geom, e2.geom);
id1 | id2 | point
-----+-----+--------------
13 | 18 | POINT(3.5 3)
(1 row)
The analysis tell us that the network has an intersection.
Preparar tablas
Additional columns to control the origin of the segments.
ALTER TABLE edges ADD old_id BIGINT;
ALTER TABLE
Adding new segments.
Calling pgr_separateCrossing and adding the new segments to the edges table.
INSERT INTO edges (old_id, geom)
SELECT id, geom
FROM pgr_separateCrossing('SELECT id, geom FROM edges');
INSERT 0 4
Update other values
In this example only cost and reverse_cost are updated, where they are
based on the length of the geometry and the directionality is kept using the
sign function.
WITH
costs AS (
SELECT e2.id, sign(e1.cost) * ST_Length(e2.geom) AS cost,
sign(e1.reverse_cost) * ST_Length(e2.geom) AS reverse_cost
FROM edges e1 JOIN edges e2 ON (e1.id = e2.old_id)
)
UPDATE edges e
SET (cost, reverse_cost) = (c.cost, c.reverse_cost)
FROM costs AS c WHERE e.id = c.id;
UPDATE 4
Actualizar la topología
Insert the new vertices if any.
WITH
new_vertex AS (
SELECT ev.*
FROM pgr_extractVertices('SELECT id, geom FROM edges WHERE old_id IS NOT NULL') ev
LEFT JOIN vertices v using(geom)
WHERE v IS NULL)
INSERT INTO vertices (in_edges, out_edges,x,y,geom)
SELECT in_edges, out_edges,x,y,geom FROM new_vertex;
INSERT 0 1
Actualizar la salida y el destino en la tabla de aristas.
/* -- set the source information */
UPDATE edges AS e
SET source = v.id, x1 = x, y1 = y
FROM vertices AS v
WHERE source IS NULL AND ST_StartPoint(e.geom) = v.geom;
UPDATE 4
/* -- set the target information */
UPDATE edges AS e
SET target = v.id, x2 = x, y2 = y
FROM vertices AS v
WHERE target IS NULL AND ST_EndPoint(e.geom) = v.geom;
UPDATE 4
The example has results
Routing from
SELECT *
FROM pgr_dijkstra('SELECT id, source, target, cost, reverse_cost FROM edges', 1, 18);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 1 | 18 | 1 | 6 | 1 | 0
2 | 2 | 1 | 18 | 3 | 7 | 1 | 1
3 | 3 | 1 | 18 | 7 | 10 | 1 | 2
4 | 4 | 1 | 18 | 8 | 12 | 1 | 3
5 | 5 | 1 | 18 | 12 | 19 | 0.5 | 4
6 | 6 | 1 | 18 | 18 | -1 | 0 | 4.5
(6 rows)
Touching edges¶
Visually the edges seem to be connected, but internally they are not.
SELECT id, ST_AsText(geom)
FROM edges where id IN (14,17);
id | st_astext
----+----------------------------------------
17 | LINESTRING(0.5 3.5,1.999999999999 3.5)
14 | LINESTRING(2 3,2 4)
(2 rows)
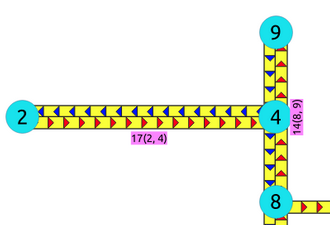
The validity of the information is application dependent.
Maybe there is a small barrier for vehicles but not for pedestrians.
Once analyzed one by one the touchings, for the ones that need a local fix, the edges need to be split.
Hay que añadir las nuevas aristas a la tabla de aristas, actualizar el resto de atributos en las nuevas aristas, eliminar las aristas antiguas y actualizar la topología de encaminamiento.
Fixing a gap¶
In this example the original edge table will be used to store the additional geometries.
An example use without results
Routing from
SELECT *
FROM pgr_dijkstra( 'SELECT id, source, target, cost, reverse_cost FROM edges', 1, 2);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
(0 rows)
Analizar la red por espacios.
WITH
deadends AS (
SELECT id AS vid, (in_edges || out_edges)[1] AS edge, geom AS vgeom
FROM vertices
WHERE array_length(in_edges || out_edges, 1) = 1
)
SELECT id, ST_AsText(geom), vid, ST_AsText(vgeom), ST_Distance(geom, vgeom)
FROM edges, deadends
WHERE id != edge AND ST_Distance(geom, vgeom) < 0.1;
id | st_astext | vid | st_astext | st_distance
----+---------------------+-----+---------------------------+-----------------------
14 | LINESTRING(2 3,2 4) | 4 | POINT(1.999999999999 3.5) | 1.000088900582341e-12
(1 row)
The analysis tell us that the network has a gap.
Preparar tablas
Additional columns to control the origin of the segments.
ALTER TABLE edges ADD old_id BIGINT;
ALTER TABLE
Adding new segments.
Calling pgr_separateTouching and adding the new segments to the edges table.
INSERT INTO edges (old_id, geom)
SELECT id, geom
FROM pgr_separateTouching('SELECT id, geom FROM edges');
INSERT 0 2
Update other values
In this example only cost and reverse_cost are updated, where they are
based on the length of the geometry and the directionality is kept using the
sign function.
WITH
costs AS (
SELECT e2.id,
sign(e1.cost) * ST_Length(e2.geom) AS cost,
sign(e1.reverse_cost) * ST_Length(e2.geom) AS reverse_cost
FROM edges e1
JOIN edges e2 ON (e1.id = e2.old_id)
)
UPDATE edges e SET (cost, reverse_cost) = (c.cost, c.reverse_cost)
FROM costs AS c
WHERE e.id = c.id;
UPDATE 2
Actualizar la topología
Insert the new vertices if any.
WITH new_vertex AS (
SELECT ev.*
FROM pgr_extractVertices('SELECT id, geom FROM edges WHERE old_id IS NOT NULL') ev
LEFT JOIN vertices v using(geom)
WHERE v IS NULL
)
INSERT INTO vertices (in_edges, out_edges,x,y,geom)
SELECT in_edges, out_edges,x,y,geom
FROM new_vertex;
INSERT 0 0
Actualizar la salida y el destino en la tabla de aristas.
/* -- set the source information */
UPDATE edges AS e
SET source = v.id, x1 = x, y1 = y
FROM vertices AS v
WHERE source IS NULL AND ST_StartPoint(e.geom) = v.geom;
UPDATE 2
/* -- set the target information */
UPDATE edges AS e
SET target = v.id, x2 = x, y2 = y
FROM vertices AS v
WHERE target IS NULL AND ST_EndPoint(e.geom) = v.geom;
UPDATE 2
The example has results
Routing from
SELECT *
FROM pgr_dijkstra('SELECT id, source, target, cost, reverse_cost FROM edges', 1, 2);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 1 | 2 | 1 | 6 | 1 | 0
2 | 2 | 1 | 2 | 3 | 7 | 1 | 1
3 | 3 | 1 | 2 | 7 | 10 | 1 | 2
4 | 4 | 1 | 2 | 8 | 19 | 0.5 | 3
5 | 5 | 1 | 2 | 4 | 17 | 1 | 3.5
6 | 6 | 1 | 2 | 2 | -1 | 0 | 4.5
(6 rows)
Conectando componentes¶
Para obtener la conectividad del grafo:
SELECT * FROM pgr_connectedComponents(
'SELECT id, source, target, cost, reverse_cost FROM edges'
);
seq | component | node
-----+-----------+------
1 | 1 | 1
2 | 1 | 3
3 | 1 | 5
4 | 1 | 6
5 | 1 | 7
6 | 1 | 8
7 | 1 | 9
8 | 1 | 10
9 | 1 | 11
10 | 1 | 12
11 | 1 | 15
12 | 1 | 16
13 | 1 | 17
14 | 2 | 2
15 | 2 | 4
16 | 13 | 13
17 | 13 | 14
(17 rows)
There are three basic ways to connect components:
Del vértice al punto inicial de la arista
Desde el vértice hasta el punto final de la arista
Del vértice al vértice más cercano de la arista
Esta solución requiere dividir el borde.
In this example pgr_separateCrossing and pgr_separateTouching will be used.
Get the connectivity
SELECT * FROM pgr_connectedComponents(
'SELECT id, source, target, cost, reverse_cost FROM edges'
);
seq | component | node
-----+-----------+------
1 | 1 | 1
2 | 1 | 3
3 | 1 | 5
4 | 1 | 6
5 | 1 | 7
6 | 1 | 8
7 | 1 | 9
8 | 1 | 10
9 | 1 | 11
10 | 1 | 12
11 | 1 | 15
12 | 1 | 16
13 | 1 | 17
14 | 2 | 2
15 | 2 | 4
16 | 13 | 13
17 | 13 | 14
(17 rows)
Preparar tablas
In this example: the edges table will need an additional column and the vertex table will be rebuilt completely.
ALTER TABLE edges ADD old_id BIGINT;
ALTER TABLE
DROP TABLE vertices;
DROP TABLE
Insert new edges
Using pgr_separateCrossing and pgr_separateTouching insert the results into the edges table.
INSERT INTO edges (old_id, geom)
SELECT id, geom FROM pgr_separateCrossing('SELECT * FROM edges')
UNION
SELECT id, geom FROM pgr_separateTouching('SELECT * FROM edges');
INSERT 0 6
Crear la tabla de vértices
Using pgr_extractVertices create the table.
CREATE TABLE vertices AS
SELECT * FROM pgr_extractVertices('SELECT id, geom FROM edges');
SELECT 18
Actualizar la topología
/* -- set the source information */
UPDATE edges AS e
SET source = v.id, x1 = x, y1 = y
FROM vertices AS v
WHERE ST_StartPoint(e.geom) = v.geom;
UPDATE 24
/* -- set the target information */
UPDATE edges AS e
SET target = v.id, x2 = x, y2 = y
FROM vertices AS v
WHERE ST_EndPoint(e.geom) = v.geom;
UPDATE 24
Update other values
In this example only cost and reverse_cost are updated, where they are
based on the length of the geometry and the directionality is kept using the
sign function.
UPDATE edges e
SET cost = ST_length(e.geom)*sign(e1.cost),
reverse_cost = ST_length(e.geom)*sign(e1.reverse_cost)
FROM edges e1
WHERE e.cost IS NULL AND e1.id = e.old_id;
UPDATE 6
SELECT * FROM pgr_connectedComponents(
'SELECT id, source, target, cost, reverse_cost FROM edges'
);
seq | component | node
-----+-----------+------
1 | 1 | 1
2 | 1 | 2
3 | 1 | 3
4 | 1 | 4
5 | 1 | 5
6 | 1 | 6
7 | 1 | 7
8 | 1 | 8
9 | 1 | 9
10 | 1 | 10
11 | 1 | 11
12 | 1 | 12
13 | 1 | 13
14 | 1 | 14
15 | 1 | 15
16 | 1 | 16
17 | 1 | 17
18 | 1 | 18
(18 rows)
Contracción de un grafo¶
El grafo puede reducirse de tamaño utilizando Contraction - Familia de funciones
El cuando contraer dependerá del tamaño del gráfico, de los tiempos de procesamiento, de la corrección de los datos, de la aplicación final o de cualquier otro factor no mencionado.
Un método bastante bueno para saber si la contracción puede ser útil es por el número de callejones sin salida y/o el número de aristas lineales.
En Contraction - Familia de funciones se describe un método completo sobre cómo contraer y cómo utilizar el grafo contraído
Callejones sin salida¶
Para obtener los callejones sin salida:
SELECT id FROM vertices
WHERE array_length(in_edges || out_edges, 1) = 1;
id
----
1
2
5
(3 rows)
Un callejón sin salida se produce cuando
El vértice es el límite de un callejón sin salida, una vía de no paso o una vía de no salida.
El vértice esta en el limite del grafo importado.
Si se importa un grafo más grande, puede que el vértice no sea un callejón sin salida.
El nodo
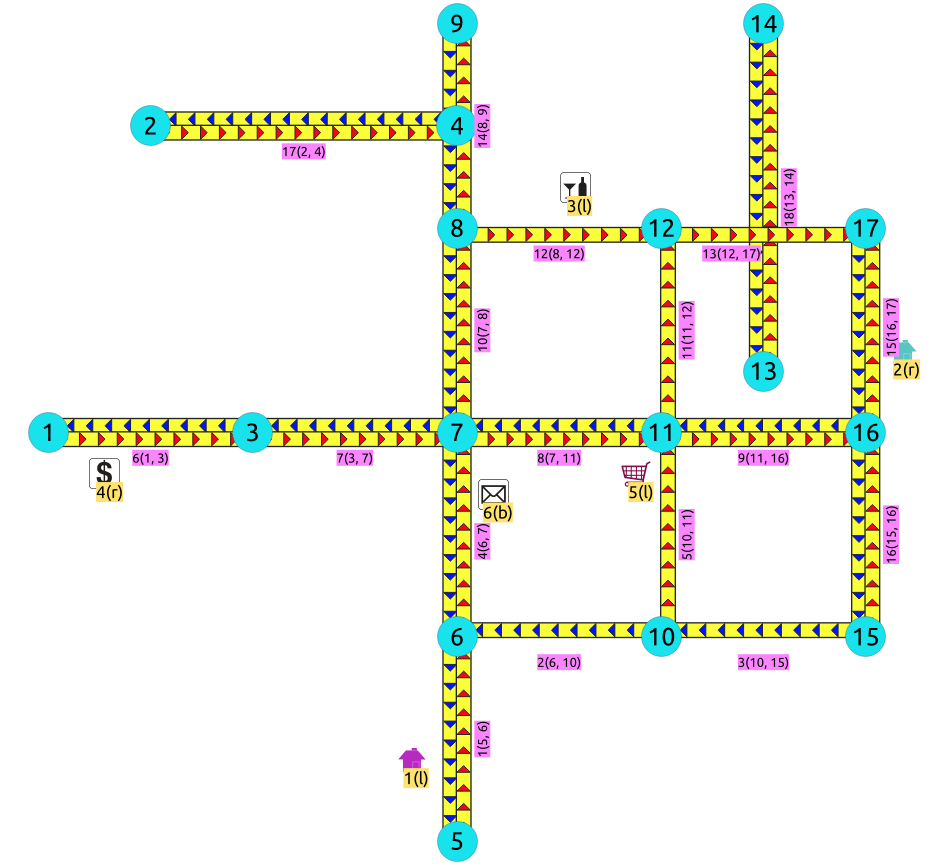
¿Es el nodo
![graph G {
1,2,4,5,9,13,14 [shape=circle;style=filled;color=lightgreen;fontsize=8;width=0.3;fixedsize=true];
3,6,7,8,10,11,12,15,16,17 [shape=circle;style=filled;color=cyan;fontsize=8;width=0.3;fixedsize=true];
5 -- 6 [label="1",fontsize=8]; 6 -- 10 [label="2",fontsize=8];
10 -- 15 [label="3",fontsize=8]; 6 -- 7 [label="4",fontsize=8];
10 -- 11 [label="5",fontsize=8]; 1 -- 3 [label="6",fontsize=8];
3 -- 7 [label="7",fontsize=8]; 7 -- 11 [label="8",fontsize=8];
11 -- 16 [label="9",fontsize=8]; 7 -- 8 [label="10",fontsize=8];
11 -- 12 [label="11",fontsize=8]; 8 -- 12 [label="12",fontsize=8];
12 -- 17 [label="13",fontsize=8]; 8 -- 9 [label="",fontsize=8];
16 -- 17 [label="15",fontsize=8]; 15 -- 16 [label="16",fontsize=8];
2 -- 4 [label="17",fontsize=8]; 13 -- 14 [label="18",fontsize=8];
1 [pos="0,2!"]; 2 [pos="0.5,3.5!"];
3 [pos="1,2!"]; 4 [pos="2,3.5!"];
5 [pos="2,0!"]; 6 [pos="2,1!"];
7 [pos="2,2!"]; 8 [pos="2,3!"];
9 [pos="2,4!"]; 10 [pos="3,1!"];
11 [pos="3,2!"]; 12 [pos="3,3!"];
13 [pos="3.5,2.3!"]; 14 [pos="3.5,4!"];
15 [pos="4,1!"]; 16 [pos="4,2!"];
17 [pos="4,3!"];
}](_images/graphviz-0efc1c6f9c1a1176ac42aaa8de0be1e9186f8539.png)
La respuesta a esta pregunta dependerá de la aplicación.
Hay un bordillo tan pequeño:
¿Eso no permite a un vehículo utilizar esa intersección visual?
¿Es la aplicación para peatones y por lo tanto el peatón puede caminar fácilmente en una acera pequeña?
¿Es la aplicación para la electricidad y las líneas eléctricas que se puede extender fácilmente en la parte superior de la acera pequeña?
¿Hay un gran acantilado y desde la vista de las águilas parece que el callejón sin salida está cerca del segmento?
Dependiendo de la respuesta, será necesario la modificación de datos.
Cuando hay muchos callejones sin salida, para acelerar el procesamiento, se pueden utilizar las funciones de Contraction - Familia de funciones para contraer el grafo.
Bordes lineales¶
Para obtener las aristas lineales:
SELECT id FROM vertices
WHERE array_length(in_edges || out_edges, 1) = 2;
id
----
3
9
13
15
16
(5 rows)
![graph G {
3,15,17 [shape=circle;style=filled;color=lightgreen;fontsize=8;width=0.3;fixedsize=true];
1,2,4,5,6,7,8,9,10,11,12,13,14,16 [shape=circle;style=filled;color=cyan;fontsize=8;width=0.3;fixedsize=true];
5 -- 6 [label="1",fontsize=8]; 6 -- 10 [label="2",fontsize=8];
10 -- 15 [label="3",fontsize=8]; 6 -- 7 [label="4",fontsize=8];
10 -- 11 [label="5",fontsize=8]; 1 -- 3 [label="6",fontsize=8];
3 -- 7 [label="7",fontsize=8]; 7 -- 11 [label="8",fontsize=8];
11 -- 16 [label="9",fontsize=8]; 7 -- 8 [label="10",fontsize=8];
11 -- 12 [label="11",fontsize=8]; 8 -- 12 [label="12",fontsize=8];
12 -- 17 [label="13",fontsize=8]; 8 -- 9 [label="",fontsize=8];
16 -- 17 [label="15",fontsize=8]; 15 -- 16 [label="16",fontsize=8];
2 -- 4 [label="17",fontsize=8]; 13 -- 14 [label="18",fontsize=8];
1 [pos="0,2!"]; 2 [pos="0.5,3.5!"];
3 [pos="1,2!"]; 4 [pos="2,3.5!"];
5 [pos="2,0!"]; 6 [pos="2,1!"];
7 [pos="2,2!"]; 8 [pos="2,3!"];
9 [pos="2,4!"]; 10 [pos="3,1!"];
11 [pos="3,2!"]; 12 [pos="3,3!"];
13 [pos="3.5,2.3!"]; 14 [pos="3.5,4!"];
15 [pos="4,1!"]; 16 [pos="4,2!"];
17 [pos="4,3!"];
}](_images/graphviz-fcaa0541303f92371c3cf508089a4be8712de558.png)
Estos vértices lineales son correctos, por ejemplo, cuando esos vértices son badenes, señales de alto y la aplicación los tiene en cuenta.
Cuando hay muchas aristas lineales, que no necesitan tomarse en cuenta, para acelerar el procesamiento se pueden utilizar las funciones Contraction - Familia de funciones para contraer el grafo.
Estructura de la función¶
Una vez realizado el trabajo de preparación del grafo anterior, es el momento de utilizar un
La forma general de una llamada a una función de pgRouting es:
pgr_<nombre>(Consultas internas, parámetros, [ Parámetros opcionales)
Donde:
Consultas internas: Son parámetros obligatorios que son
TEXTque contienen consultas SQL.Parámetros: Parámetros obligatorios adicionales que necesita la función.
Parámetros opcionales: Son parámetros nombrados no obligatorios que tienen un valor por defecto cuando se omiten.
Los parámetros obligatorios son parámetros de posición, los parámetros opcionales son parámetros nombrados.
Por ejemplo, para esta firma pgr_dijkstra:
pgr_dijkstra(SQL de aristas, salidas, destinos, [directed])
-
Es el primer parámetro.
Es obligatorio.
Es una consulta interna.
No tiene nombre, por lo que SQL de aristas da una idea del tipo de consulta interna que hay que utilizar
vid inical:
Es el segundo parámetro.
Es obligatorio.
No tiene nombre, por lo que salida da una idea de lo que debe contener el valor del segundo parámetro.
destino
Es el tercer parámetro.
Es obligatorio.
No tiene nombre, por lo que destino da una idea de lo que debe contener el valor del tercer parámetro
directedEs el cuarto parámetro.
Es opcional.
Tiene un nombre.
La descripción completa de los parámetros se encuentra en la sección Parámetros de cada función.
Sobrecargas de funciones¶
Una función puede tener diferentes sobrecargas. Las más comunes se llaman:
Dependiendo de la sobrecarga, los tipos de los parámetros cambian.
Uno: CUALQUIER-ENTERO
Muchos:
ARRAY[CUALQUIER-ENTERO]
Dependiendo de la función, las sobrecargas pueden variar. Pero el concepto de cambio de tipo de parámetro sigue siendo el mismo.
Uno a Uno¶
Cuando se rutea desde:
Desde un vértice inicial
al un vértice final
Uno a Muchos¶
Cuando se rutea desde:
Desde un vértice inicial
a los vértices finales many
Muchos a Uno¶
Cuando se rutea desde:
Desde muchos vértices iniciales
al un vértice final
Muchos a Muchos¶
Cuando se rutea desde:
Desde muchos vértices iniciales
a los vértices finales many
Combinaciones¶
Cuando se rutea desde:
A partir de muchos diferentes vértices de inicio
a muchos diferentes vértices finales
Cada tupla especifica un par de vértices iniciales y un vértice final
Los usuarios pueden definir las combinaciones como deseen.
Necesita una SQL de combinaciones
Consultas Internas¶
Existen varios tipos de consultas internas válidas y también las columnas devueltas dependen de la función. El tipo de consulta interna dependerá de los requisitos de la función. Para simplificar la variedad de tipos, se utiliza ANY-INTEGER y ANY-NUMERICAL.
Donde:
- ENTEROS:
SMALLINT, INTEGER, BIGINT- FLOTANTES:
SMALLINT, INTEGER, BIGINT, REAL, FLOAT
SQL aristas¶
General¶
SQL de aristas para
Algunas funciones no categorizadas
Columna |
Tipo |
x Defecto |
Descripción |
|---|---|---|---|
|
ENTEROS |
Identificador de la arista. |
|
|
ENTEROS |
Identificador del primer vértice de la arista. |
|
|
ENTEROS |
Identificador del segundo vértice de la arista. |
|
|
FLOTANTES |
Peso de la arista ( |
|
|
FLOTANTES |
-1 |
Peso de la arista (
|
Donde:
- ENTEROS:
SMALLINT,INTEGER,BIGINT- FLOTANTES:
SMALLINT,INTEGER,BIGINT,REAL,FLOAT
General sin id¶
SQL de aristas para
Columna |
Tipo |
x Defecto |
Descripción |
|---|---|---|---|
|
ENTEROS |
Identificador del primer vértice de la arista. |
|
|
ENTEROS |
Identificador del segundo vértice de la arista. |
|
|
FLOTANTES |
Peso de la arista ( |
|
|
FLOTANTES |
-1 |
Peso de la arista (
|
Donde:
- ENTEROS:
SMALLINT,INTEGER,BIGINT- FLOTANTES:
SMALLINT,INTEGER,BIGINT,REAL,FLOAT
General con (X,Y)¶
SQL de aristas para
Parámetro |
Tipo |
x Defecto |
Descripción |
|---|---|---|---|
|
ENTEROS |
Identificador de la arista. |
|
|
ENTEROS |
Identificador del primer vértice de la arista. |
|
|
ENTEROS |
Identificador del segundo vértice de la arista. |
|
|
FLOTANTES |
Peso de la arista (
|
|
|
FLOTANTES |
-1 |
Peso de la arista (
|
|
FLOTANTES |
Coordenada X del vértice |
|
|
FLOTANTES |
Coordenada Y del vértice |
|
|
FLOTANTES |
Coordenada X del vértice |
|
|
FLOTANTES |
Coordenada Y del vértice |
Donde:
- ENTEROS:
SMALLINT,INTEGER,BIGINT- FLOTANTES:
SMALLINT,INTEGER,BIGINT,REAL,FLOAT
Flujo¶
SQL de aristas para Flow - Familia de funciones
SQL de aristas para
Columna |
Tipo |
x Defecto |
Descripción |
|---|---|---|---|
|
ENTEROS |
Identificador de la arista. |
|
|
ENTEROS |
Identificador del primer vértice de la arista. |
|
|
ENTEROS |
Identificador del segundo vértice de la arista. |
|
|
ENTEROS |
Peso de la arista ( |
|
|
ENTEROS |
-1 |
Peso de la arista (
|
Donde:
- ENTEROS:
SMALLINT,INTEGER,BIGINT- FLOTANTES:
SMALLINT,INTEGER,BIGINT,REAL,FLOAT
SQL de aristas para las siguientes funciones de Flow - Familia de funciones
Columna |
Tipo |
x Defecto |
Descripción |
|---|---|---|---|
|
ENTEROS |
Identificador de la arista. |
|
|
ENTEROS |
Identificador del primer vértice de la arista. |
|
|
ENTEROS |
Identificador del segundo vértice de la arista. |
|
|
ENTEROS |
Capacidad de la arista (
|
|
|
ENTEROS |
-1 |
Capacidad de la arista (
|
|
FLOTANTES |
Peso de la arista ( |
|
|
FLOTANTES |
Peso de la arista ( |
Donde:
- ENTEROS:
SMALLINT,INTEGER,BIGINT- FLOTANTES:
SMALLINT,INTEGER,BIGINT,REAL,FLOAT
SQL Combinaciones¶
Utilizado en combinación firmas
Parámetro |
Tipo |
Descripción |
|---|---|---|
|
ENTEROS |
Identificador del vértice de partida. |
|
ENTEROS |
Identificador del vértice de llegada. |
Donde:
- ENTEROS:
SMALLINT,INTEGER,BIGINT
SQL restricciones¶
Columna |
Tipo |
Descripción |
|---|---|---|
|
|
Secuencia de identificadores de aristas que forman un camino que no se permite tomar. - Arreglos vacios o |
|
FLOTANTES |
Costo de tomar el camino prohibido. |
Donde:
- ENTEROS:
SMALLINT,INTEGER,BIGINT- FLOTANTES:
SMALLINT,INTEGER,BIGINT,REAL,FLOAT
SQL de puntos¶
SQL de puntos para
Parámetro |
Tipo |
x Defecto |
Descripción |
|---|---|---|---|
|
ENTEROS |
valor |
Identificador del punto.
|
|
ENTEROS |
Identificador de la arista «más cercana» al punto. |
|
|
FLOTANTES |
El valor en <0,1> que indica la posición relativa desde el primer punto de la arista. |
|
|
|
|
Valor en [
|
Donde:
- ENTEROS:
SMALLINT,INTEGER,BIGINT- FLOTANTES:
SMALLINT,INTEGER,BIGINT,REAL,FLOAT
Parámetros¶
El parámetro principal de la mayoría de las funciones pgRouting es una consulta que selecciona las aristas del grafo.
Parámetro |
Tipo |
Descripción |
|---|---|---|
|
SQL de aristas descritas más adelante. |
Dependiendo de la familia o categoría de una función tendrá parámetros adicionales, algunos de ellos son obligatorios y otros opcionales.
Los parámetros obligatorios no tienen nombre y deben indicarse en el orden requerido. Los parámetros opcionales son parámetros con nombre y tendrán un valor por defecto.
Párametros para las funciones Via¶
Parámetro |
Tipo |
x Defecto |
Descripción |
|---|---|---|---|
|
Consulta SQL como se describe. |
||
vértices |
|
Arreglo ordenado de identificadores de vértices que serán visitados. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Para las funciones de TRSP¶
Columna |
Tipo |
Descripción |
|---|---|---|
|
Consulta SQL como se describe. |
|
|
Consulta SQL como se describe. |
|
|
SQL de combinaciones como se describe a abajo |
|
salida |
ENTEROS |
Identificador del vértice de partida. |
salidas |
|
Arreglo de identificadores de vértices destino. |
destino |
ENTEROS |
Identificador del vértice de partida. |
destinos |
|
Arreglo de identificadores de vértices destino. |
Donde:
- ENTEROS:
SMALLINT,INTEGER,BIGINT
Columnas de resultados¶
Hay varios tipos de columnas devueltas que dependen de la función.
Columnas de resultados para una ruta¶
Se utiliza en funciones que devuelven una solución de ruta
Devuelve el conjunto de (seq, path_seq [, start_vid] [, end_vid], node, edge, cost, agg_cost)
Columna |
Tipo |
Descripción |
|---|---|---|
|
|
Valor secuencial a partir de 1. |
|
|
Posición relativa en la ruta. Tiene el valor 1 para el inicio de una ruta. |
|
|
Identificador del vértice inicial. Se devuelve cuando hay varias vetrices iniciales en la consulta. |
|
|
Identificador del vértice final. Se devuelve cuando hay varios vértices finales en la consulta. |
|
|
Identificador del nodo en la ruta de |
|
|
Identificador de la arista utilizado para ir del |
|
|
Costo para atravesar desde |
|
|
Costo agregado desde |
Se utiliza en las funciones siguientes:
Devuelve el conjunto de (seq, path_seq [, start_pid] [, end_pid], node, edge, cost, agg_cost)
Columna |
Tipo |
Descripción |
|---|---|---|
|
|
Valor secuencial a partir de 1. |
|
|
Posición relativa en la ruta.
|
|
|
Identificador del vértice/punto inicial de la ruta.
|
|
|
Identificador d vértice/punto final del camino.
|
|
|
Identificador del nodo en la ruta de
|
|
|
Identificador de la arsita utilizada para ir del
|
|
|
Costo para atravesar desde
|
|
|
Costo agregado desde
|
Se utiliza en las funciones siguientes:
Regresa (seq, path_seq, start_vid, end_vid, node, edge, cost, agg_cost)
Columna |
Tipo |
Descripción |
|---|---|---|
|
|
Valor secuencial a partir de 1. |
|
|
Posición relativa en la ruta. Tiene el valor 1 para el inicio de una ruta. |
|
|
Identificador del vértice inicial de la ruta actual. |
|
|
Identificador del vértice final de la ruta actual. |
|
|
Identificador del nodo en la ruta de |
|
|
Identificador de la arista utilizado para ir del |
|
|
Costo para atravesar desde |
|
|
Costo agregado desde |
Varias rutas¶
Selectivo para múltiples rutas.¶
Las columnas dependen de la llamada a la función.
Conjunto de (seq, path_id, path_seq [, start_vid] [, end_vid], node, edge, cost, agg_cost)
Columna |
Tipo |
Descripción |
|---|---|---|
|
|
Valor secuencial a partir de 1. |
|
|
Identificador del camino.
|
|
|
Posición relativa en la ruta. Tiene el valor 1 para el inicio de una ruta. |
|
|
Identificador del vértice inicial. Se devuelve cuando hay varias vetrices iniciales en la consulta. |
|
|
Identificador del vértice final. Se devuelve cuando hay varios vértices finales en la consulta. |
|
|
Identificador del nodo en la ruta de |
|
|
Identificador de la arista utilizado para ir del |
|
|
Costo para atravesar desde |
|
|
Costo agregado desde |
No selectivo para rutas múltiples¶
Independientemente de la llamada, se devuelven todas las columnas.
Devuelve el conjunto de (seq, path_id, path_seq, start_vid, end_vid, node, edge, cost, agg_cost)
Columna |
Tipo |
Descripción |
|---|---|---|
|
|
Valor secuencial a partir de 1. |
|
|
Identificador del camino.
|
|
|
Posición relativa en la ruta. Tiene el valor 1 para el inicio de una ruta. |
|
|
Identificador del vértice de salida. |
|
|
Identificador del vértice final. |
|
|
Identificador del nodo en la ruta de |
|
|
Identificador de la arista utilizado para ir del |
|
|
Costo para atravesar desde |
|
|
Costo agregado desde |
Columnas de resultados de las funciones de costes¶
Se utiliza en
Conjunto de (start_vid, end_vid, agg_cost)
Columna |
Tipo |
Descripción |
|---|---|---|
|
|
Identificador del vértice de salida. |
|
|
Identificador del vértice final. |
|
|
Costo afregado desde |
Nota
Cuando las columnas del vértice inicial o del destino continen valores negativos, el identificador es para un Punto.
Columnas de resultados para funciones de flujo¶
SQL de aristas para lo siguiente
Columna |
Tipo |
Descripción |
|---|---|---|
seq |
|
Valor secuencial a partir de 1. |
arista |
|
Identificador de la arista en la consulta original(edges_sql). |
start_vid |
|
Identificador del primer vértice de la arista. |
end_vid |
|
Identificador del segundo vértice de la arista. |
flujo |
|
Flujo a través del arista en la dirección ( |
residual_capacity |
|
Capacidad residual del arista en la dirección ( |
SQL de aristas para las siguientes funciones de Flow - Familia de funciones
Columna |
Tipo |
Descripción |
|---|---|---|
seq |
|
Valor secuencial a partir de 1. |
arista |
|
Identificador de la arista en la consulta original(edges_sql). |
origen |
|
Identificador del primer vértice de la arista. |
objetivo |
|
Identificador del segundo vértice de la arista. |
flujo |
|
Flujo a través de la arista en la dirección (origen, destino). |
residual_capacity |
|
Capacidad residual de la arista en la dirección (origen, destino). |
costo |
|
El costo de enviar este flujo a través de la arista en la dirección (origen, destino). |
agg_cost |
|
El costo agregado. |
Columnas de resultados para funciones de árbol de expansión¶
SQL de aristas para lo siguiente
Regresa el conjunto de (edge, cost)
Columna |
Tipo |
Descripción |
|---|---|---|
|
|
Identificador de la arista. |
|
|
Coste para atravezar el borde. |
Consejos de Rendimiento¶
Para las funciones de Ruteo¶
Para obtener resultados más rápidos, delimitar las consultas a un área de interés para el ruteo.
En este ejemplo, usar una consulta SQL interna que no incluya algunas aristas en la función de ruteo y dentro del área de los resultados.
Dada esta área:
SELECT id, source, target, cost, reverse_cost
FROM edges
WHERE geom && (
SELECT st_buffer(geom, 1) as myarea
FROM edges where id = 6) ORDER BY id;
id | source | target | cost | reverse_cost
----+--------+--------+------+--------------
1 | 5 | 6 | 1 | 1
2 | 6 | 10 | -1 | 1
4 | 6 | 7 | 1 | 1
6 | 1 | 3 | 1 | 1
7 | 3 | 7 | 1 | 1
8 | 7 | 11 | 1 | 1
10 | 7 | 8 | 1 | 1
12 | 8 | 12 | 1 | -1
14 | 8 | 9 | 1 | 1
20 | 8 | 4 | 0.5 | 0.5
(10 rows)
Calcular una ruta:
SELECT * FROM pgr_dijkstra($$
SELECT id, source, target, cost, reverse_cost
FROM edges
WHERE geom && (
SELECT st_buffer(geom, 1) AS myarea
FROM edges WHERE id = 6)$$,
7, 8);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 7 | 8 | 7 | 10 | 1 | 0
2 | 2 | 7 | 8 | 8 | -1 | 0 | 1
(2 rows)
Cómo contribuir¶
Wiki
Edita una página existente Wiki de pgRouting.
O crea una nueva página Wiki
Crear una página en el Wiki de pgRouting
Asigne al título un nombre apropiado
Agregando Funcionalidad a pgRouting
Consultar la documentation de desarrolladores
Índices y tablas