pgRouting Concepts

This is a simple guide that go through some of the steps for getting started with pgRouting. This guide covers:

Graphs

Graph definition

A graph is an ordered pair \(G = (V ,E)\) where:

• \(V\) is a set of vertices, also called nodes.

• \(E \subseteq \{( u, v ) \mid u , v \in V \}\)

There are different kinds of graphs:

• Undirected graph

  • \(E \subseteq \{( u, v ) \mid u , v \in V\}\)

• Undirected simple graph

  • \(E \subseteq \{( u, v ) \mid u , v \in V, u \neq v\}\)

• Directed graph

  • \(E \subseteq \{( u, v ) \mid (u , v) \in (V X V) \}\)

• Directed simple graph

  • \(E \subseteq \{( u, v ) \mid (u , v) \in (V X V), u \neq v\}\)

Graphs:

• Do not have geometries.

• Some graph theory problems require graphs to have weights, called cost in pgRouting.

In pgRouting there are several ways to represent a graph on the database:

• With cost

  • (id, source, target, cost)

• With cost and reverse_cost

  • (id, source, target, cost, reverse_cost)

Where:

Column	Description
id	Identifier of the edge. Requirement to use the database in a consistent. manner.
source	Identifier of a vertex.
target	Identifier of a vertex.
cost	Weight of the edge (source, target): When negative the edge (source, target) do not exist on the graph. cost must exist in the query.
reverse_cost	Weight of the edge (target, source) When negative the edge (target, source) do not exist on the graph.

The decision of the graph to be directed or undirected is done when executing a pgRouting algorithm.

Graph with cost

The weighted directed graph, \(G_d(V,E)\):

• Graph data is obtained with a query

  SELECT id, source, target, cost FROM edges

• the set of edges \(E\)

  • \(E = \{(source_{id}, target_{id}, cost_{id}) \text{ when } cost_{id} \ge 0 \}\)

  • Edges where cost is non negative are part of the graph.

• the set of vertices \(V\)

  • \(V = \{source_{id} \cup target_{id}\}\)

  • All vertices in source and target are part of the graph.

Directed graph

In a directed graph the edge \((source_{id}, target_{id}, cost_{id})\) has directionality: \(source_{id} \rightarrow target_{id}\)

For the following data:

SELECT *
FROM (VALUES (1, 1, 2, 5), (2, 1, 3, -3))
     AS t(id, source, target, cost);
 id | source | target | cost
----+--------+--------+------
  1 |      1 |      2 |    5
  2 |      1 |      3 |   -3
(2 rows)

Edge \(2\) (\(1 \rightarrow 3\)) is not part of the graph.

The data is representing the following graph:

Undirected graph

In an undirected graph the edge \((source_{id}, target_{id}, cost_{id})\) does not have directionality: \(source_{id} \frac{\;\;\;\;\;}{} target_{id}\)

• In terms of a directed graph is like having two edges: \(source_{id} \leftrightarrow target_{id}\)

For the following data:

SELECT *
FROM (VALUES (1, 1, 2, 5), (2, 1, 3, -3))
     AS t(id, source, target, cost);
 id | source | target | cost
----+--------+--------+------
  1 |      1 |      2 |    5
  2 |      1 |      3 |   -3
(2 rows)

Edge \(2\) (\(1 \frac{\;\;\;\;\;}{} 3\)) is not part of the graph.

The data is representing the following graph:

Graph with cost and reverse_cost

The weighted directed graph, \(G_d(V,E)\), is defined by:

• Graph data is obtained with a query

  SELECT id, source, target, cost, reverse_cost FROM edges

• The set of edges \(E\):

  • \(E = \begin{split} \begin{align} & {\{(source_{id}, target_{id}, cost_{id}) \text{ when } cost_{id} >=0 \}} \\ & \cup \\ & {\{(target_{id}, source_{id}, reverse\_cost_{id}) \text{ when } reverse\_cost_{id} >=0 \}} \end{align} \end{split}\)

  • Edges \((source \rightarrow target)\) where cost is non negative are part of the graph.

  • Edges \((target \rightarrow source)\) where reverse_cost is non negative are part of the graph.

• The set of vertices \(V\):

  • \(V = \{source_{id} \cup target_{id}\}\)

  • All vertices in source and target are part of the graph.

Directed graph

In a directed graph both edges have directionality

• edge \((source_{id}, target_{id}, cost_{id})\) has directionality: \(source_{id} \rightarrow target_{id}\)

• edge \((target_{id}, source_{id}, reverse\_cost_{id})\) has directionality: \(target_{id} \rightarrow source_{id}\)

For the following data:

SELECT *
FROM (VALUES (1, 1, 2, 5, 2), (2, 1, 3, -3, 4), (3, 2, 3, 7, -1))
     AS t(id, source, target, cost, reverse_cost);
 id | source | target | cost | reverse_cost
----+--------+--------+------+--------------
  1 |      1 |      2 |    5 |            2
  2 |      1 |      3 |   -3 |            4
  3 |      2 |      3 |    7 |           -1
(3 rows)

Edges not part of the graph:

• \(2\) (\(1 \rightarrow 3\))

• \(3\) (\(3 \rightarrow 2\))

The data is representing the following graph:

Undirected graph

In a directed graph both edges do not have directionality

• Edge \((source_{id}, target_{id}, cost_{id})\) is \(source_{id} \frac{\;\;\;\;\;}{} target_{id}\)

• Edge \((target_{id}, source_{id}, reverse\_cost_{id})\) is \(target_{id} \frac{\;\;\;\;\;}{} source_{id}\)

• In terms of a directed graph is like having four edges:

  • \(source_i \leftrightarrow target_i\)

  • \(target_i \leftrightarrow source_i\)

For the following data:

SELECT *
FROM (VALUES (1, 1, 2, 5, 2), (2, 1, 3, -3, 4), (3, 2, 3, 7, -1))
     AS t(id, source, target, cost, reverse_cost);
 id | source | target | cost | reverse_cost
----+--------+--------+------+--------------
  1 |      1 |      2 |    5 |            2
  2 |      1 |      3 |   -3 |            4
  3 |      2 |      3 |    7 |           -1
(3 rows)

Edges not part of the graph:

• \(2\) (\(1 \frac{\;\;\;\;\;}{} 3\))

• \(3\) (\(3 \frac{\;\;\;\;\;}{} 2\))

The data is representing the following graph:

Graphs without geometries

Personal relationships, genealogy, file dependency problems can be solved using pgRouting. Those problems, normally, do not come with geometries associated with the graph.

Wiki example

Solve the example problem taken from wikipedia):

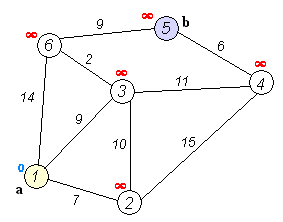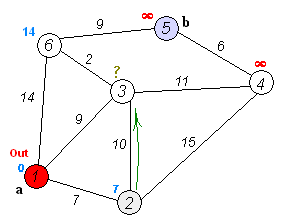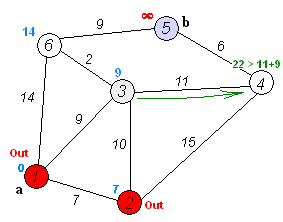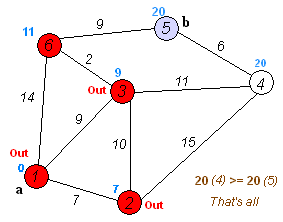
Where:

• Problem is to find the shortest path from \(1\) to \(5\).

• Is an undirected graph.

• Although visually looks like to have geometries, the drawing is not to scale.

  • No geometries associated to the vertices or edges

• Has 6 vertices \(\{1,2,3,4,5,6\}\)

• Has 9 edges:

  \(\begin{split} \begin{align} E = & \{(1,2,7), (1,3,9), (1,6,14), \\ & (2,3,10), (2,4,13), \\ & (3,4,11), (3,6,2), \\ & (4,5,6), \\ & (5,6,9) \} \end{align} \end{split}\)

• The graph can be represented in many ways for example:

Prepare the database

Create a database for the example, access the database and install pgRouting:

$ createdb wiki
$ psql wiki
wiki =# CREATE EXTENSION pgRouting CASCADE;

Create a table

The basic elements needed to perform basic routing on an undirected graph are:

Column	Type	Description
id	ANY-INTEGER	Identifier of the edge.
source	ANY-INTEGER	Identifier of the first end point vertex of the edge.
target	ANY-INTEGER	Identifier of the second end point vertex of the edge.
cost	ANY-NUMERICAL	Weight of the edge (source, target)

Where:

ANY-INTEGER:

SMALLINT, INTEGER, BIGINT

ANY-NUMERICAL:

SMALLINT, INTEGER, BIGINT, REAL, FLOAT

Using this table design for this example:

CREATE TABLE wiki (
  id SERIAL,
  source INTEGER,
  target INTEGER,
  cost INTEGER);
CREATE TABLE

Insert the data

INSERT INTO wiki (source, target, cost) VALUES
(1, 2, 7),  (1, 3, 9), (1, 6, 14),
(2, 3, 10), (2, 4, 15),
(3, 6, 2),  (3, 4, 11),
(4, 5, 6),
(5, 6, 9);
INSERT 0 9

Find the shortest path

To solve this example pgr_dijkstra is used:

SELECT * FROM pgr_dijkstra(
  'SELECT id, source, target, cost FROM wiki',
  1, 5, false);
 seq | path_seq | node | edge | cost | agg_cost
-----+----------+------+------+------+----------
   1 |        1 |    1 |    2 |    9 |        0
   2 |        2 |    3 |    6 |    2 |        9
   3 |        3 |    6 |    9 |    9 |       11
   4 |        4 |    5 |   -1 |    0 |       20
(4 rows)

To go from \(1\) to \(5\) the path goes thru the following vertices: \(1 \rightarrow 3 \rightarrow 6 \rightarrow 5\)

Vertex information

To obtain the vertices information, use pgr_extractVertices – Proposed

SELECT id, in_edges, out_edges
FROM pgr_extractVertices('SELECT id, source, target FROM wiki');
 id | in_edges | out_edges
----+----------+-----------
  3 | {2,4}    | {6,7}
  5 | {8}      | {9}
  4 | {5,7}    | {8}
  2 | {1}      | {4,5}
  1 |          | {1,2,3}
  6 | {3,6,9}  |
(6 rows)

Graphs with geometries

Create a routing Database

The first step is to create a database and load pgRouting in the database.

Typically create a database for each project.

Once having the database to work in, load your data and build the routing application in that database.

createdb sampledata
psql sampledata -c "CREATE EXTENSION pgrouting CASCADE"

Load Data

There are several ways to load your data into pgRouting.

• Manually creating a database.

  • Graphs without geometries

  • Sample Data: a small graph used on the documentation examples

• Using osm2pgrouting

There are various open source tools that can help, like:

shp2pgsql:

• postgresql shapefile loader

ogr2ogr:

• vector data conversion utility

osm2pgsql:

• load OSM data into postgresql

Please note that these tools will not import the data in a structure compatible with pgRouting and when this happens the topology needs to be adjusted.

• Breakup a segments on each segment-segment intersection

• When missing, add columns and assign values to source, target, cost, reverse_cost.

• Connect a disconnected graph.

• Create the complete graph topology

• Create one or more graphs based on the application to be developed.

  • Create a contracted graph for the high speed roads

  • Create graphs per state/country

In few words:

Prepare the graph

What and how to prepare the graph, will depend on the application and/or on the quality of the data and/or on how close the information is to have a topology usable by pgRouting and/or some other factors not mentioned.

The steps to prepare the graph involve geometry operations using PostGIS and some others involve graph operations like pgr_contraction to contract a graph.

The workshop has a step by step on how to prepare a graph using Open Street Map data, for a small application.

The use of indexes on the database design in general:

• Have the geometries indexed.

• Have the identifiers columns indexed.

Please consult the PostgreSQL documentation and the PostGIS documentation.

Build a routing topology

The basic information to use the majority of the pgRouting functions id, source, target, cost, [reverse_cost] is what in pgRouting is called the routing topology.

reverse_cost is optional but strongly recommended to have in order to reduce the size of the database due to the size of the geometry columns. Having said that, in this documentation reverse_cost is used in this documentation.

When the data comes with geometries and there is no routing topology, then this step is needed.

All the start and end vertices of the geometries need an identifier that is to be stored in a source and target columns of the table of the data. Likewise, cost and reverse_cost need to have the value of traversing the edge in both directions.

If the columns do not exist they need to be added to the table in question. (see ALTER TABLE)

The function pgr_extractVertices – Proposed is used to create a vertices table based on the edge identifier and the geometry of the edge of the graph.

Finally using the data stored on the vertices tables the source and target are filled up.

See Sample Data for an example for building a topology.

Data coming from OSM and using osm2pgrouting as an import tool, comes with the routing topology. See an example of using osm2pgrouting on the workshop.

Adjust costs

For this example the cost and reverse_cost values are going to be the double of the length of the geometry.

Update costs to length of geometry

Suppose that cost and reverse_cost columns in the sample data represent:

• \(1\) when the edge exists in the graph

• \(-1\) when the edge does not exist in the graph

Using that information updating to the length of the geometries:

UPDATE edges SET
cost = sign(cost) * ST_length(geom) * 2,
reverse_cost = sign(reverse_cost) * ST_length(geom) * 2;
UPDATE 18

Which gives the following results:

SELECT id, cost, reverse_cost FROM edges;
 id |        cost        |    reverse_cost
----+--------------------+--------------------
  6 |                  2 |                  2
  7 |                  2 |                  2
  4 |                  2 |                  2
  5 |                  2 |                 -2
  8 |                  2 |                  2
 12 |                  2 |                 -2
 11 |                  2 |                 -2
 10 |                  2 |                  2
 17 |     2.999999999998 |     2.999999999998
 14 |                  2 |                  2
 18 | 3.4000000000000004 | 3.4000000000000004
 13 |                  2 |                 -2
 15 |                  2 |                  2
 16 |                  2 |                  2
  9 |                  2 |                  2
  3 |                 -2 |                  2
  1 |                  2 |                  2
  2 |                 -2 |                  2
(18 rows)

Note that to be able to follow the documentation examples, everything is based on the original graph.

Returning to the original data:

UPDATE edges SET
cost = sign(cost),
reverse_cost = sign(reverse_cost);
UPDATE 18

Update costs based on codes

Other datasets, can have a column with values like

• FT vehicle flow on the direction of the geometry

• TF vehicle flow opposite of the direction of the geometry

• B vehicle flow on both directions

Preparing a code column for the example:

ALTER TABLE edges ADD COLUMN direction TEXT;
ALTER TABLE
UPDATE edges SET
direction = CASE WHEN (cost>0 AND reverse_cost>0) THEN 'B'
           WHEN (cost>0 AND reverse_cost<0) THEN 'FT'
           WHEN (cost<0 AND reverse_cost>0) THEN 'TF'
           ELSE '' END;
UPDATE 18

Adjusting the costs based on the codes:

UPDATE edges SET
cost = CASE WHEN (direction = 'B' OR direction = 'FT')
       THEN ST_length(geom) * 2
       ELSE -1 END,
reverse_cost = CASE WHEN (direction = 'B' OR direction = 'TF')
       THEN ST_length(geom) * 2
       ELSE -1 END;
UPDATE 18

Which gives the following results:

SELECT id, cost, reverse_cost FROM edges;
 id |        cost        |    reverse_cost
----+--------------------+--------------------
  6 |                  2 |                  2
  7 |                  2 |                  2
  4 |                  2 |                  2
  5 |                  2 |                 -1
  8 |                  2 |                  2
 12 |                  2 |                 -1
 11 |                  2 |                 -1
 10 |                  2 |                  2
 17 |     2.999999999998 |     2.999999999998
 14 |                  2 |                  2
 18 | 3.4000000000000004 | 3.4000000000000004
 13 |                  2 |                 -1
 15 |                  2 |                  2
 16 |                  2 |                  2
  9 |                  2 |                  2
  3 |                 -1 |                  2
  1 |                  2 |                  2
  2 |                 -1 |                  2
(18 rows)

Returning to the original data:

UPDATE edges SET
cost = sign(cost),
reverse_cost = sign(reverse_cost);
UPDATE 18
ALTER TABLE edges DROP COLUMN direction;
ALTER TABLE

Check the Routing Topology

There are lots of possible problems in a graph.

• The data used may not have been designed with routing in mind.

• A graph has some very specific requirements.

• The graph is disconnected.

• There are unwanted intersections.

• The graph is too large and needs to be contracted.

• A sub graph is needed for the application.

• and many other problems that the pgRouting user, that is the application developer might encounter.

Crossing edges

To get the crossing edges:

SELECT a.id, b.id
FROM edges AS a, edges AS b
WHERE a.id < b.id AND st_crosses(a.geom, b.geom);
 id | id
----+----
 13 | 18
(1 row)

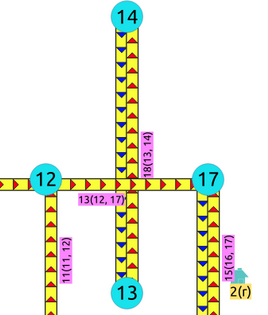
That information is correct, for example, when in terms of vehicles, is it a tunnel or bride crossing over another road.

It might be incorrect, for example:

1. When it is actually an intersection of roads, where vehicles can make turns.

2. When in terms of electrical lines, the electrical line is able to switch roads even on a tunnel or bridge.

When it is incorrect, it needs fixing:

1. For vehicles and pedestrians

   • If the data comes from OSM and was imported to the database using osm2pgrouting, the fix needs to be done in the OSM portal and the data imported again.

   • In general when the data comes from a supplier that has the data prepared for routing vehicles, and there is a problem, the data is to be fixed from the supplier

2. For very specific applications

   • The data is correct when from the point of view of routing vehicles or pedestrians.

   • The data needs a local fix for the specific application.

Once analyzed one by one the crossings, for the ones that need a local fix, the edges need to be split.

SELECT ST_AsText((ST_Dump(ST_Split(a.geom, b.geom))).geom)
FROM edges AS a, edges AS b
WHERE a.id = 13 AND b.id = 18
UNION
SELECT ST_AsText((ST_Dump(ST_Split(b.geom, a.geom))).geom)
FROM edges AS a, edges AS b
WHERE a.id = 13 AND b.id = 18;
         st_astext
---------------------------
 LINESTRING(3.5 2.3,3.5 3)
 LINESTRING(3 3,3.5 3)
 LINESTRING(3.5 3,4 3)
 LINESTRING(3.5 3,3.5 4)
(4 rows)

The new edges need to be added to the edges table, the rest of the attributes need to be updated in the new edges, the old edges need to be removed and the routing topology needs to be updated.

Adding split edges

For each pair of crossing edges a process similar to this one must be performed.

The columns inserted and the way are calculated are based on the application. For example, if the edges have a trait name, then that column is to be copied.

For pgRouting calculations

• factor based on the position of the intersection of the edges can be used to adjust the cost and reverse_cost columns.

• Capacity information, used on the Flow - Family of functions functions does not need to change when splitting edges.

WITH
first_edge AS (
  SELECT (ST_Dump(ST_Split(a.geom, b.geom))).path[1],
    (ST_Dump(ST_Split(a.geom, b.geom))).geom,
    ST_LineLocatePoint(a.geom,ST_Intersection(a.geom,b.geom)) AS factor
  FROM edges AS a, edges AS b
  WHERE a.id = 13 AND b.id = 18),
first_segments AS (
  SELECT path, first_edge.geom,
    capacity, reverse_capacity,
    CASE WHEN path=1 THEN factor * cost
         ELSE (1 - factor) * cost END AS cost,
    CASE WHEN path=1 THEN factor * reverse_cost
         ELSE (1 - factor) * reverse_cost END AS reverse_cost
  FROM first_edge , edges WHERE id = 13),
second_edge AS (
  SELECT (ST_Dump(ST_Split(b.geom, a.geom))).path[1],
    (ST_Dump(ST_Split(b.geom, a.geom))).geom,
    ST_LineLocatePoint(b.geom,ST_Intersection(a.geom,b.geom)) AS factor
  FROM edges AS a, edges AS b
  WHERE a.id = 13 AND b.id = 18),
second_segments AS (
  SELECT path, second_edge.geom,
    capacity, reverse_capacity,
    CASE WHEN path=1 THEN factor * cost
         ELSE (1 - factor) * cost END AS cost,
    CASE WHEN path=1 THEN factor * reverse_cost
         ELSE (1 - factor) * reverse_cost END AS reverse_cost
  FROM second_edge , edges WHERE id = 18),
all_segments AS (
  SELECT * FROM first_segments
  UNION
  SELECT * FROM second_segments)
INSERT INTO edges
  (capacity, reverse_capacity,
    cost, reverse_cost,
    x1, y1, x2, y2,
    geom)
(SELECT capacity, reverse_capacity, cost, reverse_cost,
  ST_X(ST_StartPoint(geom)), ST_Y(ST_StartPoint(geom)),
  ST_X(ST_EndPoint(geom)), ST_Y(ST_EndPoint(geom)),
  geom
  FROM all_segments);
INSERT 0 4

Adding new vertices

After adding all the split edges required by the application, the newly created vertices need to be added to the vertices table.

INSERT INTO vertices (in_edges, out_edges, x, y, geom)
(SELECT nv.in_edges, nv.out_edges, nv.x, nv.y, nv.geom
FROM pgr_extractVertices('SELECT id, geom FROM edges') AS nv
LEFT JOIN vertices AS v USING(geom) WHERE v.geom IS NULL);
INSERT 0 1

Updating edges topology

/* -- set the source information */
UPDATE edges AS e
SET source = v.id
FROM vertices AS v
WHERE source IS NULL AND ST_StartPoint(e.geom) = v.geom;
UPDATE 4
/* -- set the target information */
UPDATE edges AS e
SET target = v.id
FROM vertices AS v
WHERE target IS NULL AND ST_EndPoint(e.geom) = v.geom;
UPDATE 4

Removing the surplus edges

Once all significant information needed by the application has been transported to the new edges, then the crossing edges can be deleted.

DELETE FROM edges WHERE id IN (13, 18);
DELETE 2

There are other options to do this task, like creating a view, or a materialized view.

Updating vertices topology

To keep the graph consistent, the vertices topology needs to be updated

UPDATE vertices AS v SET
in_edges = nv.in_edges, out_edges = nv.out_edges
FROM (SELECT * FROM pgr_extractVertices('SELECT id, geom FROM edges')) AS nv
WHERE v.geom = nv.geom;
UPDATE 18

Checking for crossing edges

There are no crossing edges on the graph.

SELECT a.id, b.id
FROM edges AS a, edges AS b
WHERE a.id < b.id AND st_crosses(a.geom, b.geom);
 id | id
----+----
(0 rows)

Disconnected graphs

To get the graph connectivity:

SELECT * FROM pgr_connectedComponents(
  'SELECT id, source, target, cost, reverse_cost FROM edges'
);
 seq | component | node
-----+-----------+------
   1 |         1 |    1
   2 |         1 |    3
   3 |         1 |    5
   4 |         1 |    6
   5 |         1 |    7
   6 |         1 |    8
   7 |         1 |    9
   8 |         1 |   10
   9 |         1 |   11
  10 |         1 |   12
  11 |         1 |   13
  12 |         1 |   14
  13 |         1 |   15
  14 |         1 |   16
  15 |         1 |   17
  16 |         1 |   18
  17 |         2 |    2
  18 |         2 |    4
(18 rows)

In this example, the component \(2\) consists of vertices \(\{2, 4\}\) and both vertices are also part of the dead end result set.

This graph needs to be connected.

Note

With the original graph of this documentation, there would be 3 components as the crossing edge in this graph is a different component.

Prepare storage for connection information

ALTER TABLE vertices ADD COLUMN component BIGINT;
ALTER TABLE
ALTER TABLE edges ADD COLUMN component BIGINT;
ALTER TABLE

Save the vertices connection information

UPDATE vertices SET component = c.component
FROM (SELECT * FROM pgr_connectedComponents(
  'SELECT id, source, target, cost, reverse_cost FROM edges'
)) AS c
WHERE id = node;
UPDATE 18

Save the edges connection information

UPDATE edges SET component = v.component
FROM (SELECT id, component FROM vertices) AS v
WHERE source = v.id;
UPDATE 20

Get the closest vertex

The closest vertex to component \(1\) is vertex \(4\). And the closest edge to vertex \(4\) is edge \(14\).

WITH
edges_sql AS (SELECT id, geom FROM edges WHERE component = 1),
point_sql AS (SELECT geom AS point FROM vertices WHERE component = 2),
results AS (
  SELECT
    id::BIGINT AS edge_id,
    ST_LineLocatePoint(geom, point) AS fraction,
    CASE WHEN ST_Intersects(ST_Buffer(geom, 2, 'side=right endcap=flat'), point)
         THEN 'r'
         ELSE 'l' END::CHAR AS side,
    geom <-> point AS distance,
    point,
    ST_MakeLine(point, ST_ClosestPoint(geom, point)) AS new_line
  FROM  edges_sql, point_sql
  WHERE ST_DWithin(geom, point, 2)
  ORDER BY geom <-> point),
prepare_cap AS (
  SELECT row_number() OVER (PARTITION BY point ORDER BY point, distance) AS rn, *
  FROM results),
cap AS (
  SELECT edge_id, fraction, side, distance, point, new_line
  FROM prepare_cap
  WHERE rn <= 1
)
SELECT edge_id, fraction, side, distance, point AS geom, new_line AS edge, id AS closest_vertex
INTO closest
FROM cap JOIN vertices ON (point = geom) ORDER BY distance LIMIT 1;
SELECT 1

The edge can be used to connect the components, using the fraction information about the edge \(14\) to split the connecting edge.

Connecting components

There are three basic ways to connect the components

• From the vertex to the starting point of the edge

• From the vertex to the ending point of the edge

• From the vertex to the closest vertex on the edge

  • This solution requires the edge to be split.

The following query shows the three ways to connect the components:

WITH
info AS (
  SELECT
    edge_id, fraction, side, distance, ce.geom, edge, v.id AS closest,
    source, target, capacity, reverse_capacity, e.geom AS e_geom
  FROM closest AS ce
  JOIN vertices AS v USING (geom)
  JOIN edges AS e ON (edge_id = e.id)
  ORDER BY distance LIMIT 1),
three_options AS (
  SELECT
    closest AS source, target, 0 AS cost, 0 AS reverse_cost,
    capacity, reverse_capacity,
    ST_X(geom) AS x1, ST_Y(geom) AS y1,
    ST_X(ST_EndPoint(e_geom)) AS x2, ST_Y(ST_EndPoint(e_geom)) AS y2,
    ST_MakeLine(geom, ST_EndPoint(e_geom)) AS geom
  FROM info

  UNION

  SELECT closest, source, 0, 0, capacity, reverse_capacity,
    ST_X(geom) AS x1, ST_Y(geom) AS y1,
    ST_X(ST_StartPoint(e_geom)) AS x2, ST_Y(ST_StartPoint(e_geom)) AS y2,
    ST_MakeLine(info.geom, ST_StartPoint(e_geom))
  FROM info
  /*
  UNION
  -- This option requires splitting the edge
  SELECT closest, NULL, 0, 0, capacity, reverse_capacity,
    ST_X(geom) AS x1, ST_Y(geom) AS y1,
    ST_X(ST_EndPoint(edge)) AS x2, ST_Y(ST_EndPoint(edge)) AS y2,
    edge
  FROM info */
  )

INSERT INTO edges
  (source, target,
    cost, reverse_cost,
    capacity, reverse_capacity,
    x1, y1, x2, y2,
    geom)
(SELECT
    source, target, cost, reverse_cost, capacity, reverse_capacity,
    x1, y1, x2, y2, geom
  FROM three_options);
INSERT 0 2

Checking components

Ignoring the edge that requires further work. The graph is now fully connected as there is only one component.

SELECT * FROM pgr_connectedComponents(
  'SELECT id, source, target, cost, reverse_cost FROM edges'
);
 seq | component | node
-----+-----------+------
   1 |         1 |    1
   2 |         1 |    2
   3 |         1 |    3
   4 |         1 |    4
   5 |         1 |    5
   6 |         1 |    6
   7 |         1 |    7
   8 |         1 |    8
   9 |         1 |    9
  10 |         1 |   10
  11 |         1 |   11
  12 |         1 |   12
  13 |         1 |   13
  14 |         1 |   14
  15 |         1 |   15
  16 |         1 |   16
  17 |         1 |   17
  18 |         1 |   18
(18 rows)

Contraction of a graph

The graph can be reduced in size using Contraction - Family of functions

When to contract will depend on the size of the graph, processing times, correctness of the data, on the final application, or any other factor not mentioned.

A fairly good method of finding out if contraction can be useful is because of the number of dead ends and/or the number of linear edges.

A complete method on how to contract and how to use the contracted graph is described on Contraction - Family of functions

Dead ends

To get the dead ends:

SELECT id FROM vertices
WHERE array_length(in_edges || out_edges, 1) = 1;
 id
----
  1
  5
  9
 13
 14
  2
  4
(7 rows)

That information is correct, for example, when the dead end is on the limit of the imported graph.

Visually node \(4\) looks to be as start/ending of 3 edges, but it is not.

Is that correct?

• Is there such a small curb:

  • That does not allow a vehicle to use that visual intersection?

  • Is the application for pedestrians and therefore the pedestrian can easily walk on the small curb?

  • Is the application for the electricity and the electrical lines than can easily be extended on top of the small curb?

• Is there a big cliff and from eagles view look like the dead end is close to the segment?

When there are many dead ends, to speed up, the Contraction - Family of functions functions can be used to divide the problem.

Linear edges

To get the linear edges:

SELECT id FROM vertices
WHERE array_length(in_edges || out_edges, 1) = 2;
 id
----
  3
 15
 17
(3 rows)

This information is correct, for example, when the application is taking into account speed bumps, stop signals.

When there are many linear edges, to speed up, the Contraction - Family of functions functions can be used to divide the problem.

Function’s structure

Once the graph preparation work has been done above, it is time to use a

The general form of a pgRouting function call is:

pgr_<name>(Inner queries, parameters, [ Optional parameters)

Where:

• Inner queries: Are compulsory parameters that are TEXT strings containing SQL queries.

• parameters: Additional compulsory parameters needed by the function.

• Optional parameters: Are non compulsory named parameters that have a default value when omitted.

The compulsory parameters are positional parameters, the optional parameters are named parameters.

For example, for this pgr_dijkstra signature:

pgr_dijkstra(Edges SQL, start vid, end vid [, directed])

• Edges SQL:

  • Is the first parameter.

  • It is compulsory.

  • It is an inner query.

  • It has no name, so Edges SQL gives an idea of what kind of inner query needs to be used

• start vid:

  • Is the second parameter.

  • It is compulsory.

  • It has no name, so start vid gives an idea of what the second parameter’s value should contain.

• end vid

  • Is the third parameter.

  • It is compulsory.

  • It has no name, so end vid gives an idea of what the third parameter’s value should contain

• directed

  • Is the fourth parameter.

  • It is optional.

  • It has a name.

The full description of the parameters are found on the Parameters section of each function.

Function’s overloads

A function might have different overloads. The most common are called:

• One to One

• One to Many

• Many to One

• Many to Many

• Combinations

Depending on the overload the parameters types change.

• One: ANY-INTEGER

• Many: ARRAY [ANY-INTEGER]

Depending of the function the overloads may vary. But the concept of parameter type change remains the same.

One to One

When routing from:

• From one starting vertex

• to one ending vertex

One to Many

When routing from:

• From one starting vertex

• to many ending vertices

Many to One

When routing from:

• From many starting vertices

• to one ending vertex

Many to Many

When routing from:

• From many starting vertices

• to many ending vertices

Combinations

When routing from:

• From many different starting vertices

• to many different ending vertices

• Every tuple specifies a pair of a start vertex and an end vertex

• Users can define the combinations as desired.

• Needs a Combinations SQL

Inner Queries

There are several kinds of valid inner queries and also the columns returned are depending of the function. Which kind of inner query will depend on the function(s) requirements. To simplify variety of types, ANY-INTEGER and ANY-NUMERICAL is used.

Where:

ANY-INTEGER:

SMALLINT, INTEGER, BIGINT

ANY-NUMERICAL:

SMALLINT, INTEGER, BIGINT, REAL, FLOAT

Edges SQL

General

Edges SQL for

• Dijkstra - Family of functions

• withPoints - Family of functions

• Bidirectional Dijkstra - Family of functions

• Components - Family of functions

• Kruskal - Family of functions

• Prim - Family of functions

• Some uncategorised functions

Column	Type	Default	Description
id	ANY-INTEGER		Identifier of the edge.
source	ANY-INTEGER		Identifier of the first end point vertex of the edge.
target	ANY-INTEGER		Identifier of the second end point vertex of the edge.
cost	ANY-NUMERICAL		Weight of the edge (source, target)
reverse_cost	ANY-NUMERICAL	-1	Weight of the edge (target, source) When negative: edge (target, source) does not exist, therefore it’s not part of the graph.

Where:

ANY-INTEGER:

SMALLINT, INTEGER, BIGINT

ANY-NUMERICAL:

SMALLINT, INTEGER, BIGINT, REAL, FLOAT

General without id

Edges SQL for

• All Pairs - Family of Functions

Column	Type	Default	Description
source	ANY-INTEGER		Identifier of the first end point vertex of the edge.
target	ANY-INTEGER		Identifier of the second end point vertex of the edge.
cost	ANY-NUMERICAL		Weight of the edge (source, target)
reverse_cost	ANY-NUMERICAL	-1	Weight of the edge (target, source) When negative: edge (target, source) does not exist, therefore it’s not part of the graph.

Where:

ANY-INTEGER:

SMALLINT, INTEGER, BIGINT

ANY-NUMERICAL:

SMALLINT, INTEGER, BIGINT, REAL, FLOAT

General with (X,Y)

Edges SQL for

• A* - Family of functions

• Bidirectional A* - Family of functions

Parameter	Type	Default	Description
id	ANY-INTEGER		Identifier of the edge.
source	ANY-INTEGER		Identifier of the first end point vertex of the edge.
target	ANY-INTEGER		Identifier of the second end point vertex of the edge.
cost	ANY-NUMERICAL		Weight of the edge (source, target) When negative: edge (source, target) does not exist, therefore it’s not part of the graph.
reverse_cost	ANY-NUMERICAL	-1	Weight of the edge (target, source), When negative: edge (target, source) does not exist, therefore it’s not part of the graph.
x1	ANY-NUMERICAL		X coordinate of source vertex.
y1	ANY-NUMERICAL		Y coordinate of source vertex.
x2	ANY-NUMERICAL		X coordinate of target vertex.
y2	ANY-NUMERICAL		Y coordinate of target vertex.

Where:

ANY-INTEGER:

SMALLINT, INTEGER, BIGINT

ANY-NUMERICAL:

SMALLINT, INTEGER, BIGINT, REAL, FLOAT

Flow

Edges SQL for Flow - Family of functions

Edges SQL for

• pgr_pushRelabel

• pgr_edmondsKarp

• pgr_boykovKolmogorov

Column	Type	Default	Description
id	ANY-INTEGER		Identifier of the edge.
source	ANY-INTEGER		Identifier of the first end point vertex of the edge.
target	ANY-INTEGER		Identifier of the second end point vertex of the edge.
capacity	ANY-INTEGER		Weight of the edge (source, target)
reverse_capacity	ANY-INTEGER	-1	Weight of the edge (target, source) When negative: edge (target, source) does not exist, therefore it’s not part of the graph.

Where:

ANY-INTEGER:

SMALLINT, INTEGER, BIGINT

ANY-NUMERICAL:

SMALLINT, INTEGER, BIGINT, REAL, FLOAT

Edges SQL for the following functions of Flow - Family of functions

• pgr_maxFlowMinCost - Experimental

• pgr_maxFlowMinCost_Cost - Experimental

Column	Type	Default	Description
id	ANY-INTEGER		Identifier of the edge.
source	ANY-INTEGER		Identifier of the first end point vertex of the edge.
target	ANY-INTEGER		Identifier of the second end point vertex of the edge.
capacity	ANY-INTEGER		Capacity of the edge (source, target) When negative: edge (target, source) does not exist, therefore it’s not part of the graph.
reverse_capacity	ANY-INTEGER	-1	Capacity of the edge (target, source) When negative: edge (target, source) does not exist, therefore it’s not part of the graph.
cost	ANY-NUMERICAL		Weight of the edge (source, target) if it exist
reverse_cost	ANY-NUMERICAL	\(-1\)	Weight of the edge (target, source) if it exist

Where:

ANY-INTEGER:

SMALLINT, INTEGER, BIGINT

ANY-NUMERICAL:

SMALLINT, INTEGER, BIGINT, REAL, FLOAT

Combinations SQL

Used on combination signatures

Parameter	Type	Description
source	ANY-INTEGER	Identifier of the departure vertex.
target	ANY-INTEGER	Identifier of the arrival vertex.

Where:

ANY-INTEGER:

SMALLINT, INTEGER, BIGINT

Restrictions SQL

Column	Type	Description
path	ARRAY [ANY-INTEGER]	Sequence of edge identifiers that form a path that is not allowed to be taken. - Empty arrays or NULL arrays are ignored. - Arrays that have a NULL element will raise an exception.
Cost	ANY-NUMERICAL	Cost of taking the forbidden path.

Where:

ANY-INTEGER:

SMALLINT, INTEGER, BIGINT

ANY-NUMERICAL:

SMALLINT, INTEGER, BIGINT, REAL, FLOAT

Points SQL

Points SQL for

• withPoints - Family of functions

Parameter	Type	Default	Description
pid	ANY-INTEGER	value	Identifier of the point. Use with positive value, as internally will be converted to negative value If column is present, it can not be NULL. If column is not present, a sequential negative value will be given automatically.
edge_id	ANY-INTEGER		Identifier of the “closest” edge to the point.
fraction	ANY-NUMERICAL		Value in <0,1> that indicates the relative postition from the first end point of the edge.
side	CHAR	b	Value in [b, r, l, NULL] indicating if the point is: In the right r, In the left l, In both sides b, NULL

Where:

ANY-INTEGER:

SMALLINT, INTEGER, BIGINT

ANY-NUMERICAL:

SMALLINT, INTEGER, BIGINT, REAL, FLOAT

Parameters

The main parameter of the majority of the pgRouting functions is a query that selects the edges of the graph.

Parameter	Type	Description
Edges SQL	TEXT	Edges SQL as described below.

Depending on the family or category of a function it will have additional parameters, some of them are compulsory and some are optional.

The compulsory parameters are nameless and must be given in the required order. The optional parameters are named parameters and will have a default value.

Parameters for the Via functions

• pgr_dijkstraVia - Proposed

Parameter	Type	Default	Description
Edges SQL	TEXT		SQL query as described.
via vertices	ARRAY [ANY-INTEGER]		Array of ordered vertices identifiers that are going to be visited.
directed	BOOLEAN	true	When true Graph is considered Directed When false the graph is considered as Undirected.
strict	BOOLEAN	false	When true if a path is missing stops and returns EMPTY SET When false ignores missing paths returning all paths found
U_turn_on_edge	BOOLEAN	true	When true departing from a visited vertex will not try to avoid using the edge used to reach it. In other words, U turn using the edge with same identifier is allowed. When false when a departing from a visited vertex tries to avoid using the edge used to reach it. In other words, U turn using the edge with same identifier is used when no other path is found.

For the TRSP functions

• pgr_trsp - Turn Restriction Shortest Path (TRSP)

Column	Type	Description
Edges SQL	TEXT	SQL query as described.
Restrictions SQL	TEXT	SQL query as described.
Combinations SQL	TEXT	Combinations SQL as described below
start vid	ANY-INTEGER	Identifier of the departure vertex.
start vids	ARRAY [ANY-INTEGER]	Array of identifiers of destination vertices.
end vid	ANY-INTEGER	Identifier of the departure vertex.
end vids	ARRAY [ANY-INTEGER]	Array of identifiers of destination vertices.

Where:

ANY-INTEGER:

SMALLINT, INTEGER, BIGINT

Return columns

There are several kinds of columns returned are depending of the function.

Return columns for a path

Used on functions that return one path solution

Returns set of (seq, path_seq [, start_vid] [, end_vid], node, edge, cost, agg_cost)

Column	Type	Description
seq	INTEGER	Sequential value starting from 1.
path_seq	INTEGER	Relative position in the path. Has value 1 for the beginning of a path.
start_vid	BIGINT	Identifier of the starting vertex. Returned when multiple starting vetrices are in the query. Many to One Many to Many
end_vid	BIGINT	Identifier of the ending vertex. Returned when multiple ending vertices are in the query. One to Many Many to Many
node	BIGINT	Identifier of the node in the path from start_vid to end_vid.
edge	BIGINT	Identifier of the edge used to go from node to the next node in the path sequence. -1 for the last node of the path.
cost	FLOAT	Cost to traverse from node using edge to the next node in the path sequence.
agg_cost	FLOAT	Aggregate cost from start_vid to node.

Used on functions the following:

• pgr_withPoints - Proposed

Returns set of (seq, path_seq [, start_pid] [, end_pid], node, edge, cost, agg_cost)

Column	Type	Description
seq	INTEGER	Sequential value starting from 1.
path_seq	INTEGER	Relative position in the path. 1 For the first row of the path.
start_pid	BIGINT	Identifier of a starting vertex/point of the path. When positive is the identifier of the starting vertex. When negative is the identifier of the starting point. Returned on Many to One and Many to Many
end_pid	BIGINT	Identifier of an ending vertex/point of the path. When positive is the identifier of the ending vertex. When negative is the identifier of the ending point. Returned on One to Many and Many to Many
node	BIGINT	Identifier of the node in the path from start_pid to end_pid. When positive is the identifier of the a vertex. When negative is the identifier of the a point.
edge	BIGINT	Identifier of the edge used to go from node to the next node in the path sequence. -1 for the last row of the path.
cost	FLOAT	Cost to traverse from node using edge to the next node in the path sequence. 0 For the first row of the path.
agg_cost	FLOAT	Aggregate cost from start_vid to node. 0 For the first row of the path.

Used on functions the following:

• pgr_dijkstraNear - Proposed

Returns (seq, path_seq, start_vid, end_vid, node, edge, cost, agg_cost)

Column	Type	Description
seq	INTEGER	Sequential value starting from 1.
path_seq	INTEGER	Relative position in the path. Has value 1 for the beginning of a path.
start_vid	BIGINT	Identifier of the starting vertex of the current path.
end_vid	BIGINT	Identifier of the ending vertex of the current path.
node	BIGINT	Identifier of the node in the path from start_vid to end_vid.
edge	BIGINT	Identifier of the edge used to go from node to the next node in the path sequence. -1 for the last node of the path.
cost	FLOAT	Cost to traverse from node using edge to the next node in the path sequence.
agg_cost	FLOAT	Aggregate cost from start_vid to node.

Multiple paths

Selective for multiple paths.

The columns depend on the function call.

Set of (seq, path_id, path_seq [, start_vid] [, end_vid], node, edge, cost, agg_cost)

Column	Type	Description
seq	INTEGER	Sequential value starting from 1.
path_id	INTEGER	Path identifier. Has value 1 for the first of a path from start_vid to end_vid.
path_seq	INTEGER	Relative position in the path. Has value 1 for the beginning of a path.
start_vid	BIGINT	Identifier of the starting vertex. Returned when multiple starting vetrices are in the query. Many to One Many to Many Combinations
end_vid	BIGINT	Identifier of the ending vertex. Returned when multiple ending vertices are in the query. One to Many Many to Many Combinations
node	BIGINT	Identifier of the node in the path from start_vid to end_vid.
edge	BIGINT	Identifier of the edge used to go from node to the next node in the path sequence. -1 for the last node of the path.
cost	FLOAT	Cost to traverse from node using edge to the next node in the path sequence.
agg_cost	FLOAT	Aggregate cost from start_vid to node.

Non selective for multiple paths

Regardless of the call, al the columns are returned.

• pgr_trsp - Turn Restriction Shortest Path (TRSP)

Returns set of (seq, path_id, path_seq, start_vid, end_vid, node, edge, cost, agg_cost)

Column	Type	Description
seq	INTEGER	Sequential value starting from 1.
path_id	INTEGER	Path identifier. Has value 1 for the first of a path from start_vid to end_vid.
path_seq	INTEGER	Relative position in the path. Has value 1 for the beginning of a path.
start_vid	BIGINT	Identifier of the starting vertex.
end_vid	BIGINT	Identifier of the ending vertex.
node	BIGINT	Identifier of the node in the path from start_vid to end_vid.
edge	BIGINT	Identifier of the edge used to go from node to the next node in the path sequence. -1 for the last node of the path.
cost	FLOAT	Cost to traverse from node using edge to the next node in the path sequence.
agg_cost	FLOAT	Aggregate cost from start_vid to node.

Return columns for cost functions

Used in the following

• Cost - Category

• Cost Matrix - Category

• All Pairs - Family of Functions

Set of (start_vid, end_vid, agg_cost)

Column	Type	Description
start_vid	BIGINT	Identifier of the starting vertex.
end_vid	BIGINT	Identifier of the ending vertex.
agg_cost	FLOAT	Aggregate cost from start_vid to end_vid.

Note

When start_vid or end_vid columns have negative values, the identifier is for a Point.

Return columns for flow functions

Edges SQL for the following

• Flow - Family of functions

Column	Type	Description
seq	INT	Sequential value starting from 1.
edge	BIGINT	Identifier of the edge in the original query (edges_sql).
start_vid	BIGINT	Identifier of the first end point vertex of the edge.
end_vid	BIGINT	Identifier of the second end point vertex of the edge.
flow	BIGINT	Flow through the edge in the direction (start_vid, end_vid).
residual_capacity	BIGINT	Residual capacity of the edge in the direction (start_vid, end_vid).

Edges SQL for the following functions of Flow - Family of functions

• pgr_maxFlowMinCost - Experimental

Column	Type	Description
seq	INT	Sequential value starting from 1.
edge	BIGINT	Identifier of the edge in the original query (edges_sql).
source	BIGINT	Identifier of the first end point vertex of the edge.
target	BIGINT	Identifier of the second end point vertex of the edge.
flow	BIGINT	Flow through the edge in the direction (source, target).
residual_capacity	BIGINT	Residual capacity of the edge in the direction (source, target).
cost	FLOAT	The cost of sending this flow through the edge in the direction (source, target).
agg_cost	FLOAT	The aggregate cost.

Return columns for spanning tree functions

Edges SQL for the following

• pgr_prim

• pgr_kruskal

Returns SET OF (edge, cost)

Column	Type	Description
edge	BIGINT	Identifier of the edge.
cost	FLOAT	Cost to traverse the edge.

Performance Tips

For the Routing functions

To get faster results bound the queries to an area of interest of routing.

In this example Use an inner query SQL that does not include some edges in the routing function and is within the area of the results.

SELECT * FROM pgr_dijkstra($$
  SELECT id, source, target, cost, reverse_cost from edges
  WHERE geom && (SELECT st_buffer(geom, 1) AS myarea
    FROM edges WHERE id = 2)$$,
  1, 2);
 seq | path_seq | node | edge | cost | agg_cost
-----+----------+------+------+------+----------
(0 rows)

How to contribute

Wiki

• Edit an existing pgRouting Wiki page.

• Or create a new Wiki page

  • Create a page on the pgRouting Wiki

  • Give the title an appropriate name

• Example

Adding Functionaity to pgRouting

Consult the developer’s documentation

Indices and tables

• Index

• Search Page