Unsupported versions:2.6 2.5 2.4 2.3 2.2 2.1 2.0
pgRouting Concepts¶
This is a simple guide that go through some of the steps for getting started with pgRouting. This guide covers:
Graphs¶
Graph definition¶
A graph is an ordered pair
There are different kinds of graphs:
Undirected graph
Undirected simple graph
Directed graph
Directed simple graph
Graphs:
Do not have geometries.
Some graph theory problems require graphs to have weights, called cost in pgRouting.
In pgRouting there are several ways to represent a graph on the database:
With
cost(
id,source,target,cost)
With
costandreverse_cost(
id,source,target,cost,reverse_cost)
Where:
Column |
Description |
|---|---|
|
Identifier of the edge. Requirement to use the database in a consistent. manner. |
|
Identifier of a vertex. |
|
Identifier of a vertex. |
|
Weight of the edge (
|
|
Weight of the edge (
|
The decision of the graph to be directed or undirected is done when executing a pgRouting algorithm.
Graph with cost¶
The weighted directed graph,
Graph data is obtained with a query
SELECT id, source, target, cost FROM edgesthe set of edges
Edges where
costis non negative are part of the graph.
the set of vertices
All vertices in
sourceandtargetare part of the graph.
Directed graph
In a directed graph the edge
For the following data:
SELECT *
FROM (VALUES (1, 1, 2, 5), (2, 1, 3, -3))
AS t(id, source, target, cost);
id | source | target | cost
----+--------+--------+------
1 | 1 | 2 | 5
2 | 1 | 3 | -3
(2 rows)
Edge
The data is representing the following graph:
![digraph G {
1 -> 2 [label="1(5)"];
3;
}](_images/graphviz-6a22e17e4c49cbe911a2c3c04aea2e93942005ce.png)
Undirected graph
In an undirected graph the edge
In terms of a directed graph is like having two edges:
For the following data:
SELECT *
FROM (VALUES (1, 1, 2, 5), (2, 1, 3, -3))
AS t(id, source, target, cost);
id | source | target | cost
----+--------+--------+------
1 | 1 | 2 | 5
2 | 1 | 3 | -3
(2 rows)
Edge
The data is representing the following graph:
![graph G {
1 -- 2 [label="1(5)"];
3;
}](_images/graphviz-a9ff7d505ee3aa8158a1f3439d4325a71f0dbcae.png)
Graph with cost and reverse_cost¶
The weighted directed graph,
Graph data is obtained with a query
SELECT id, source, target, cost, reverse_cost FROM edgesThe set of edges
Edges
costis non negative are part of the graph.Edges
reverse_costis non negative are part of the graph.
The set of vertices
All vertices in
sourceandtargetare part of the graph.
Directed graph
In a directed graph both edges have directionality
edge
edge
For the following data:
SELECT *
FROM (VALUES (1, 1, 2, 5, 2), (2, 1, 3, -3, 4), (3, 2, 3, 7, -1))
AS t(id, source, target, cost, reverse_cost);
id | source | target | cost | reverse_cost
----+--------+--------+------+--------------
1 | 1 | 2 | 5 | 2
2 | 1 | 3 | -3 | 4
3 | 2 | 3 | 7 | -1
(3 rows)
Edges not part of the graph:
The data is representing the following graph:
![digraph G {
1 -> 2 [label="1(5)"];
2 -> 1 [label="1(2)"];
3 -> 1 [label="2(4)"];
2 -> 3 [label="3(7)"];
}](_images/graphviz-cf2723f26bd1c3ee60f314423c76e21eb5708d4e.png)
Undirected graph
In a directed graph both edges do not have directionality
Edge
Edge
In terms of a directed graph is like having four edges:
For the following data:
SELECT *
FROM (VALUES (1, 1, 2, 5, 2), (2, 1, 3, -3, 4), (3, 2, 3, 7, -1))
AS t(id, source, target, cost, reverse_cost);
id | source | target | cost | reverse_cost
----+--------+--------+------+--------------
1 | 1 | 2 | 5 | 2
2 | 1 | 3 | -3 | 4
3 | 2 | 3 | 7 | -1
(3 rows)
Edges not part of the graph:
The data is representing the following graph:
![graph G {
1 -- 2 [label="1(5)"];
2 -- 1 [label="1(2)"];
3 -- 1 [label="2(4)"];
2 -- 3 [label="3(7)"];
}](_images/graphviz-7cf300b7d69445756b30b2135af90e936a5dd9e4.png)
Graphs without geometries¶
Personal relationships, genealogy, file dependency problems can be solved using pgRouting. Those problems, normally, do not come with geometries associated with the graph.
Wiki example¶
Solve the example problem taken from wikipedia):
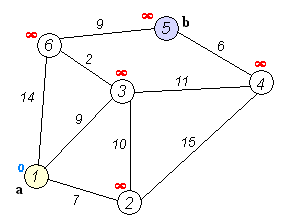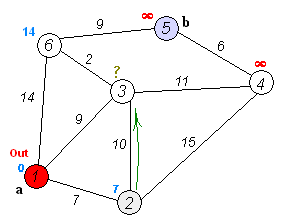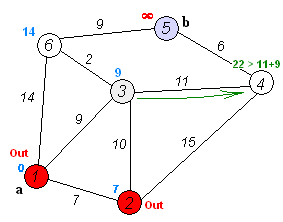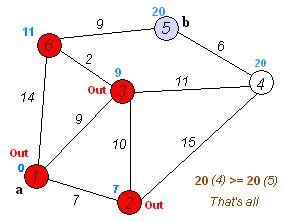
Where:
Problem is to find the shortest path from
Is an undirected graph.
Although visually looks like to have geometries, the drawing is not to scale.
No geometries associated to the vertices or edges
Has 6 vertices
Has 9 edges:
The graph can be represented in many ways for example:
![graph G {
rankdir="LR";
1 [color="red"];
5 [color="green"];
1 -- 2 [label="(7)"];
5 -- 6 [label="(9)"];
1 -- 3 [label="(9)"];
1 -- 6 [label="(14)"];
2 -- 3 [label="(10)"];
2 -- 4 [label="(13)"];
3 -- 4 [label="(11)"];
3 -- 6 [label="(2)"];
4 -- 5 [label="(6)"];
}](_images/graphviz-aa83b370a30d7a5c2be123929174e31044bca152.png)
Prepare the database¶
Create a database for the example, access the database and install pgRouting:
$ createdb wiki
$ psql wiki
wiki =# CREATE EXTENSION pgRouting CASCADE;
Create a table¶
The basic elements needed to perform basic routing on an undirected graph are:
Column |
Type |
Description |
|---|---|---|
|
ANY-INTEGER |
Identifier of the edge. |
|
ANY-INTEGER |
Identifier of the first end point vertex of the edge. |
|
ANY-INTEGER |
Identifier of the second end point vertex of the edge. |
|
ANY-NUMERICAL |
Weight of the edge ( |
Where:
- ANY-INTEGER:
SMALLINT, INTEGER, BIGINT
- ANY-NUMERICAL:
SMALLINT, INTEGER, BIGINT, REAL, FLOAT
Using this table design for this example:
CREATE TABLE wiki (
id SERIAL,
source INTEGER,
target INTEGER,
cost INTEGER);
CREATE TABLE
Insert the data¶
INSERT INTO wiki (source, target, cost) VALUES
(1, 2, 7), (1, 3, 9), (1, 6, 14),
(2, 3, 10), (2, 4, 15),
(3, 6, 2), (3, 4, 11),
(4, 5, 6),
(5, 6, 9);
INSERT 0 9
Find the shortest path¶
To solve this example pgr_dijkstra is used:
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost FROM wiki',
1, 5, false);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 1 | 5 | 1 | 2 | 9 | 0
2 | 2 | 1 | 5 | 3 | 6 | 2 | 9
3 | 3 | 1 | 5 | 6 | 9 | 9 | 11
4 | 4 | 1 | 5 | 5 | -1 | 0 | 20
(4 rows)
To go from
![graph G {
rankdir="LR";
1 [color="red"];
5 [color="green"];
1 -- 2 [label="(7)"];
5 -- 6 [label="(9)", color="blue"];
1 -- 3 [label="(9)", color="blue"];
1 -- 6 [label="(14)"];
2 -- 3 [label="(10)"];
2 -- 4 [label="(13)"];
3 -- 4 [label="(11)"];
3 -- 6 [label="(2)", color="blue"];
4 -- 5 [label="(6)"];
}](_images/graphviz-2be84fbb8166d4e067f5592a16b83c30776ea85c.png)
Vertex information¶
To obtain the vertices information, use pgr_extractVertices
SELECT id, in_edges, out_edges
FROM pgr_extractVertices('SELECT id, source, target FROM wiki');
id | in_edges | out_edges
----+----------+-----------
3 | {2,4} | {6,7}
5 | {8} | {9}
4 | {5,7} | {8}
2 | {1} | {4,5}
1 | | {1,2,3}
6 | {3,6,9} |
(6 rows)
Graphs with geometries¶
Create a routing Database¶
The first step is to create a database and load pgRouting in the database.
Typically create a database for each project.
Once having the database to work in, load your data and build the routing application in that database.
createdb sampledata
psql sampledata -c "CREATE EXTENSION pgrouting CASCADE"
Load Data¶
There are several ways to load your data into pgRouting.
Manually creating a database.
Sample Data: a small graph used in the documentation examples
Using osm2pgrouting
There are various open source tools that can help, like:
- shp2pgsql:
postgresql shapefile loader
- ogr2ogr:
vector data conversion utility
- osm2pgsql:
load OSM data into postgresql
Please note that these tools will not import the data in a structure compatible with pgRouting and when this happens the topology needs to be adjusted.
Breakup a segments on each segment-segment intersection
When missing, add columns and assign values to
source,target,cost,reverse_cost.Connect a disconnected graph.
Create the complete graph topology
Create one or more graphs based on the application to be developed.
Create a contracted graph for the high speed roads
Create graphs per state/country
In few words:
Prepare the graph
What and how to prepare the graph, will depend on the application and/or on the quality of the data and/or on how close the information is to have a topology usable by pgRouting and/or some other factors not mentioned.
The steps to prepare the graph involve geometry operations using PostGIS and some others involve graph operations like pgr_contraction to contract a graph.
The workshop has a step by step on how to prepare a graph using Open Street Map data, for a small application.
The use of indexes on the database design in general:
Have the geometries indexed.
Have the identifiers columns indexed.
Please consult the PostgreSQL documentation and the PostGIS documentation.
Build a routing topology¶
The basic information to use the majority of the pgRouting functions id,
source, target, cost, [reverse_cost] is what in pgRouting is called the
routing topology.
reverse_cost is optional but strongly recommended to have in order to reduce
the size of the database due to the size of the geometry columns.
Having said that, in this documentation reverse_cost is used in this
documentation.
When the data comes with geometries and there is no routing topology, then this step is needed.
All the start and end vertices of the geometries need an identifier that is to
be stored in a source and target columns of the table of the data.
Likewise, cost and reverse_cost need to have the value of traversing the
edge in both directions.
If the columns do not exist they need to be added to the table in question. (see ALTER TABLE)
The function pgr_extractVertices is used to create a vertices table based on the edge identifier and the geometry of the edge of the graph.
SELECT * INTO vertices
FROM pgr_extractVertices('SELECT id, geom FROM edges ORDER BY id');
SELECT 18
Finally using the data stored on the vertices tables the source and
target are filled up.
/* -- set the source information */
UPDATE edges AS e
SET source = v.id, x1 = x, y1 = y
FROM vertices AS v
WHERE ST_StartPoint(e.geom) = v.geom;
UPDATE 24
/* -- set the target information */
UPDATE edges AS e
SET target = v.id, x2 = x, y2 = y
FROM vertices AS v
WHERE ST_EndPoint(e.geom) = v.geom;
UPDATE 24
Data coming from OSM and using osm2pgrouting as an import tool, comes with
the routing topology. See an example of using osm2pgrouting on the workshop.
Adjust costs¶
For this example the cost and reverse_cost values are going to be the
double of the length of the geometry.
Update costs to length of geometry¶
Suppose that cost and reverse_cost columns in the sample data represent:
Using that information updating to the length of the geometries:
UPDATE edges SET
cost = sign(cost) * ST_length(geom) * 2,
reverse_cost = sign(reverse_cost) * ST_length(geom) * 2;
UPDATE 18
Which gives the following results:
SELECT id, cost, reverse_cost FROM edges;
id | cost | reverse_cost
----+--------------------+--------------------
6 | 2 | 2
7 | 2 | 2
4 | 2 | 2
5 | 2 | -2
8 | 2 | 2
12 | 2 | -2
11 | 2 | -2
10 | 2 | 2
17 | 2.999999999998 | 2.999999999998
14 | 2 | 2
18 | 3.4000000000000004 | 3.4000000000000004
13 | 2 | -2
15 | 2 | 2
16 | 2 | 2
9 | 2 | 2
3 | -2 | 2
1 | 2 | 2
2 | -2 | 2
(18 rows)
Note that to be able to follow the documentation examples, everything is based on the original graph.
Returning to the original data:
UPDATE edges SET
cost = sign(cost),
reverse_cost = sign(reverse_cost);
UPDATE 18
Update costs based on codes¶
Other datasets, can have a column with values like
FTvehicle flow on the direction of the geometryTFvehicle flow opposite of the direction of the geometryBvehicle flow on both directions
Preparing a code column for the example:
ALTER TABLE edges ADD COLUMN direction TEXT;
ALTER TABLE
UPDATE edges SET
direction = CASE WHEN (cost>0 AND reverse_cost>0) THEN 'B' /* both ways */
WHEN (cost>0 AND reverse_cost<0) THEN 'FT' /* direction of the LINESSTRING */
WHEN (cost<0 AND reverse_cost>0) THEN 'TF' /* reverse direction of the LINESTRING */
ELSE '' END;
UPDATE 18
/* unknown */
Adjusting the costs based on the codes:
UPDATE edges SET
cost = CASE WHEN (direction = 'B' OR direction = 'FT')
THEN ST_length(geom) * 2
ELSE -1 END,
reverse_cost = CASE WHEN (direction = 'B' OR direction = 'TF')
THEN ST_length(geom) * 2
ELSE -1 END;
UPDATE 18
Which gives the following results:
SELECT id, cost, reverse_cost FROM edges;
id | cost | reverse_cost
----+--------------------+--------------------
6 | 2 | 2
7 | 2 | 2
4 | 2 | 2
5 | 2 | -1
8 | 2 | 2
12 | 2 | -1
11 | 2 | -1
10 | 2 | 2
17 | 2.999999999998 | 2.999999999998
14 | 2 | 2
18 | 3.4000000000000004 | 3.4000000000000004
13 | 2 | -1
15 | 2 | 2
16 | 2 | 2
9 | 2 | 2
3 | -1 | 2
1 | 2 | 2
2 | -1 | 2
(18 rows)
Returning to the original data:
UPDATE edges SET
cost = sign(cost),
reverse_cost = sign(reverse_cost);
UPDATE 18
ALTER TABLE edges DROP COLUMN direction;
ALTER TABLE
Check the Routing Topology¶
There are lots of possible problems in a graph.
The data used may not have been designed with routing in mind.
A graph has some very specific requirements.
The graph is disconnected.
There are unwanted intersections.
The graph is too large and needs to be contracted.
A sub graph is needed for the application.
and many other problems that the pgRouting user, that is the application developer might encounter.
Crossing edges¶
To get the crossing edges:
SELECT a.id, b.id
FROM edges AS a, edges AS b
WHERE a.id < b.id AND st_crosses(a.geom, b.geom);
id | id
----+----
13 | 18
(1 row)
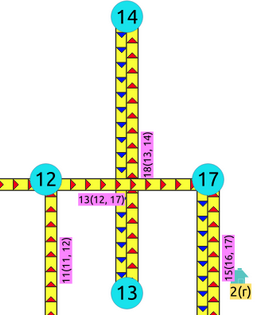
That information is correct, for example, when in terms of vehicles, is it a tunnel or bridge crossing over another road.
It might be incorrect, for example:
When it is actually an intersection of roads, where vehicles can make turns.
When in terms of electrical lines, the electrical line is able to switch roads even on a tunnel or bridge.
When it is incorrect, it needs fixing:
For vehicles and pedestrians
If the data comes from OSM and was imported to the database using
osm2pgrouting, the fix needs to be done in the OSM portal and the data imported again.In general when the data comes from a supplier that has the data prepared for routing vehicles, and there is a problem, the data is to be fixed from the supplier
For very specific applications
The data is correct when from the point of view of routing vehicles or pedestrians.
The data needs a local fix for the specific application.
Once analyzed one by one the crossings, for the ones that need a local fix, the edges need to be split.
The new edges need to be added to the edges table, the rest of the attributes need to be updated in the new edges, the old edges need to be removed and the routing topology needs to be updated.
Fixing an intersection¶
In this example the original edge table will be used to store the additional geometries.
An example use without results
Routing from
SELECT *
FROM pgr_dijkstra('SELECT id, source, target, cost, reverse_cost FROM edges', 1, 18);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
(0 rows)
Analyze the network for intersections.
SELECT
e1.id id1, e2.id id2,
ST_AsText(ST_Intersection(e1.geom, e2.geom)) AS point
FROM edges e1, edges e2
WHERE e1.id < e2.id AND ST_Crosses(e1.geom, e2.geom);
id1 | id2 | point
-----+-----+--------------
13 | 18 | POINT(3.5 3)
(1 row)
The analysis tell us that the network has an intersection.
Prepare tables
Additional columns to control the origin of the segments.
ALTER TABLE edges ADD old_id BIGINT;
ALTER TABLE
Adding new segments.
Calling pgr_separateCrossing and adding the new segments to the edges table.
INSERT INTO edges (old_id, geom)
SELECT id, geom
FROM pgr_separateCrossing('SELECT id, geom FROM edges');
INSERT 0 4
Update other values
In this example only cost and reverse_cost are updated, where they are
based on the length of the geometry and the directionality is kept using the
sign function.
WITH
costs AS (
SELECT e2.id, sign(e1.cost) * ST_Length(e2.geom) AS cost,
sign(e1.reverse_cost) * ST_Length(e2.geom) AS reverse_cost
FROM edges e1 JOIN edges e2 ON (e1.id = e2.old_id)
)
UPDATE edges e
SET (cost, reverse_cost) = (c.cost, c.reverse_cost)
FROM costs AS c WHERE e.id = c.id;
UPDATE 4
Update the topology
Insert the new vertices if any.
WITH
new_vertex AS (
SELECT ev.*
FROM pgr_extractVertices('SELECT id, geom FROM edges WHERE old_id IS NOT NULL') ev
LEFT JOIN vertices v using(geom)
WHERE v IS NULL)
INSERT INTO vertices (in_edges, out_edges,x,y,geom)
SELECT in_edges, out_edges,x,y,geom FROM new_vertex;
INSERT 0 1
Update source and target information on the edges table.
/* -- set the source information */
UPDATE edges AS e
SET source = v.id, x1 = x, y1 = y
FROM vertices AS v
WHERE source IS NULL AND ST_StartPoint(e.geom) = v.geom;
UPDATE 4
/* -- set the target information */
UPDATE edges AS e
SET target = v.id, x2 = x, y2 = y
FROM vertices AS v
WHERE target IS NULL AND ST_EndPoint(e.geom) = v.geom;
UPDATE 4
The example has results
Routing from
SELECT *
FROM pgr_dijkstra('SELECT id, source, target, cost, reverse_cost FROM edges', 1, 18);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 1 | 18 | 1 | 6 | 1 | 0
2 | 2 | 1 | 18 | 3 | 7 | 1 | 1
3 | 3 | 1 | 18 | 7 | 10 | 1 | 2
4 | 4 | 1 | 18 | 8 | 12 | 1 | 3
5 | 5 | 1 | 18 | 12 | 19 | 0.5 | 4
6 | 6 | 1 | 18 | 18 | -1 | 0 | 4.5
(6 rows)
Touching edges¶
Visually the edges seem to be connected, but internally they are not.
SELECT id, ST_AsText(geom)
FROM edges where id IN (14,17);
id | st_astext
----+----------------------------------------
17 | LINESTRING(0.5 3.5,1.999999999999 3.5)
14 | LINESTRING(2 3,2 4)
(2 rows)
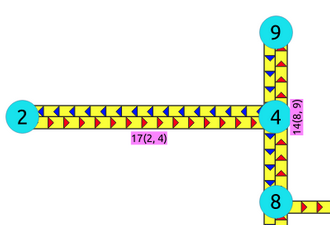
The validity of the information is application dependent.
Maybe there is a small barrier for vehicles but not for pedestrians.
Once analyzed one by one the touchings, for the ones that need a local fix, the edges need to be split.
The new edges need to be added to the edges table, the rest of the attributes need to be updated in the new edges, the old edges need to be removed and the routing topology needs to be updated.
Fixing a gap¶
In this example the original edge table will be used to store the additional geometries.
An example use without results
Routing from
SELECT *
FROM pgr_dijkstra( 'SELECT id, source, target, cost, reverse_cost FROM edges', 1, 2);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
(0 rows)
Analyze the network for gaps.
WITH
deadends AS (
SELECT id AS vid, (in_edges || out_edges)[1] AS edge, geom AS vgeom
FROM vertices
WHERE array_length(in_edges || out_edges, 1) = 1
)
SELECT id, ST_AsText(geom), vid, ST_AsText(vgeom), ST_Distance(geom, vgeom)
FROM edges, deadends
WHERE id != edge AND ST_Distance(geom, vgeom) < 0.1;
id | st_astext | vid | st_astext | st_distance
----+---------------------+-----+---------------------------+-----------------------
14 | LINESTRING(2 3,2 4) | 4 | POINT(1.999999999999 3.5) | 1.000088900582341e-12
(1 row)
The analysis tell us that the network has a gap.
Prepare tables
Additional columns to control the origin of the segments.
ALTER TABLE edges ADD old_id BIGINT;
ALTER TABLE
Adding new segments.
Calling pgr_separateTouching and adding the new segments to the edges table.
INSERT INTO edges (old_id, geom)
SELECT id, geom
FROM pgr_separateTouching('SELECT id, geom FROM edges');
INSERT 0 2
Update other values
In this example only cost and reverse_cost are updated, where they are
based on the length of the geometry and the directionality is kept using the
sign function.
WITH
costs AS (
SELECT e2.id,
sign(e1.cost) * ST_Length(e2.geom) AS cost,
sign(e1.reverse_cost) * ST_Length(e2.geom) AS reverse_cost
FROM edges e1
JOIN edges e2 ON (e1.id = e2.old_id)
)
UPDATE edges e SET (cost, reverse_cost) = (c.cost, c.reverse_cost)
FROM costs AS c
WHERE e.id = c.id;
UPDATE 2
Update the topology
Insert the new vertices if any.
WITH new_vertex AS (
SELECT ev.*
FROM pgr_extractVertices('SELECT id, geom FROM edges WHERE old_id IS NOT NULL') ev
LEFT JOIN vertices v using(geom)
WHERE v IS NULL
)
INSERT INTO vertices (in_edges, out_edges,x,y,geom)
SELECT in_edges, out_edges,x,y,geom
FROM new_vertex;
INSERT 0 0
Update source and target information on the edges table.
/* -- set the source information */
UPDATE edges AS e
SET source = v.id, x1 = x, y1 = y
FROM vertices AS v
WHERE source IS NULL AND ST_StartPoint(e.geom) = v.geom;
UPDATE 2
/* -- set the target information */
UPDATE edges AS e
SET target = v.id, x2 = x, y2 = y
FROM vertices AS v
WHERE target IS NULL AND ST_EndPoint(e.geom) = v.geom;
UPDATE 2
The example has results
Routing from
SELECT *
FROM pgr_dijkstra('SELECT id, source, target, cost, reverse_cost FROM edges', 1, 2);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 1 | 2 | 1 | 6 | 1 | 0
2 | 2 | 1 | 2 | 3 | 7 | 1 | 1
3 | 3 | 1 | 2 | 7 | 10 | 1 | 2
4 | 4 | 1 | 2 | 8 | 19 | 0.5 | 3
5 | 5 | 1 | 2 | 4 | 17 | 1 | 3.5
6 | 6 | 1 | 2 | 2 | -1 | 0 | 4.5
(6 rows)
Connecting components¶
To get the graph connectivity:
SELECT * FROM pgr_connectedComponents(
'SELECT id, source, target, cost, reverse_cost FROM edges'
);
seq | component | node
-----+-----------+------
1 | 1 | 1
2 | 1 | 3
3 | 1 | 5
4 | 1 | 6
5 | 1 | 7
6 | 1 | 8
7 | 1 | 9
8 | 1 | 10
9 | 1 | 11
10 | 1 | 12
11 | 1 | 15
12 | 1 | 16
13 | 1 | 17
14 | 2 | 2
15 | 2 | 4
16 | 13 | 13
17 | 13 | 14
(17 rows)
There are three basic ways to connect components:
From the vertex to the starting point of the edge
From the vertex to the ending point of the edge
From the vertex to the closest vertex on the edge
This solution requires the edge to be split.
In this example pgr_separateCrossing and pgr_separateTouching will be used.
Get the connectivity
SELECT * FROM pgr_connectedComponents(
'SELECT id, source, target, cost, reverse_cost FROM edges'
);
seq | component | node
-----+-----------+------
1 | 1 | 1
2 | 1 | 3
3 | 1 | 5
4 | 1 | 6
5 | 1 | 7
6 | 1 | 8
7 | 1 | 9
8 | 1 | 10
9 | 1 | 11
10 | 1 | 12
11 | 1 | 15
12 | 1 | 16
13 | 1 | 17
14 | 2 | 2
15 | 2 | 4
16 | 13 | 13
17 | 13 | 14
(17 rows)
Prepare tables
In this example: the edges table will need an additional column and the vertex table will be rebuilt completely.
ALTER TABLE edges ADD old_id BIGINT;
ALTER TABLE
DROP TABLE vertices;
DROP TABLE
Insert new edges
Using pgr_separateCrossing and pgr_separateTouching insert the results into the edges table.
INSERT INTO edges (old_id, geom)
SELECT id, geom FROM pgr_separateCrossing('SELECT * FROM edges')
UNION
SELECT id, geom FROM pgr_separateTouching('SELECT * FROM edges');
INSERT 0 6
Create the vertices table
Using pgr_extractVertices create the table.
CREATE TABLE vertices AS
SELECT * FROM pgr_extractVertices('SELECT id, geom FROM edges');
SELECT 18
Update the topology
/* -- set the source information */
UPDATE edges AS e
SET source = v.id, x1 = x, y1 = y
FROM vertices AS v
WHERE ST_StartPoint(e.geom) = v.geom;
UPDATE 24
/* -- set the target information */
UPDATE edges AS e
SET target = v.id, x2 = x, y2 = y
FROM vertices AS v
WHERE ST_EndPoint(e.geom) = v.geom;
UPDATE 24
Update other values
In this example only cost and reverse_cost are updated, where they are
based on the length of the geometry and the directionality is kept using the
sign function.
UPDATE edges e
SET cost = ST_length(e.geom)*sign(e1.cost),
reverse_cost = ST_length(e.geom)*sign(e1.reverse_cost)
FROM edges e1
WHERE e.cost IS NULL AND e1.id = e.old_id;
UPDATE 6
SELECT * FROM pgr_connectedComponents(
'SELECT id, source, target, cost, reverse_cost FROM edges'
);
seq | component | node
-----+-----------+------
1 | 1 | 1
2 | 1 | 2
3 | 1 | 3
4 | 1 | 4
5 | 1 | 5
6 | 1 | 6
7 | 1 | 7
8 | 1 | 8
9 | 1 | 9
10 | 1 | 10
11 | 1 | 11
12 | 1 | 12
13 | 1 | 13
14 | 1 | 14
15 | 1 | 15
16 | 1 | 16
17 | 1 | 17
18 | 1 | 18
(18 rows)
Contraction of a graph¶
The graph can be reduced in size using Contraction - Family of functions
When to contract will depend on the size of the graph, processing times, correctness of the data, on the final application, or any other factor not mentioned.
A fairly good method of finding out if contraction can be useful is because of the number of dead ends and/or the number of linear edges.
A complete method on how to contract and how to use the contracted graph is described on Contraction - Family of functions
Dead ends¶
To get the dead ends:
SELECT id FROM vertices
WHERE array_length(in_edges || out_edges, 1) = 1;
id
----
1
2
5
(3 rows)
A dead end happens when
The vertex is the limit of a cul-de-sac, a no-through road or a no-exit road.
The vertex is on the limit of the imported graph.
If a larger graph is imported then the vertex might not be a dead end
Node
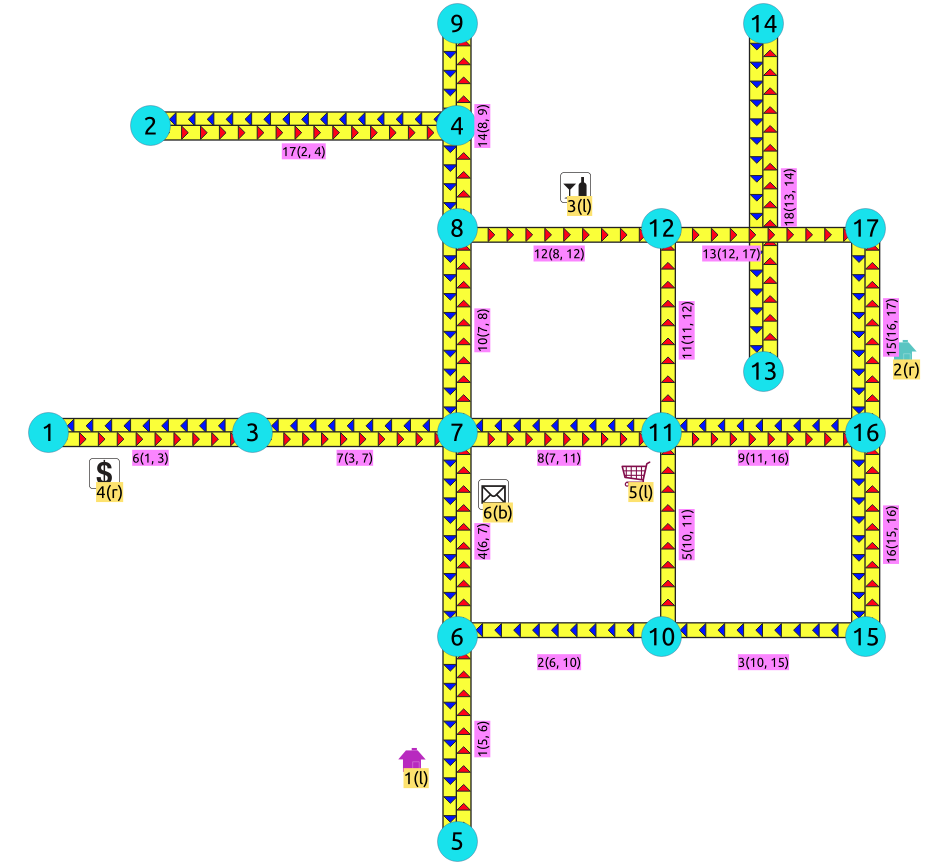
Is node
![graph G {
1,2,4,5,9,13,14 [shape=circle;style=filled;color=lightgreen;fontsize=8;width=0.3;fixedsize=true];
3,6,7,8,10,11,12,15,16,17 [shape=circle;style=filled;color=cyan;fontsize=8;width=0.3;fixedsize=true];
5 -- 6 [label="1",fontsize=8]; 6 -- 10 [label="2",fontsize=8];
10 -- 15 [label="3",fontsize=8]; 6 -- 7 [label="4",fontsize=8];
10 -- 11 [label="5",fontsize=8]; 1 -- 3 [label="6",fontsize=8];
3 -- 7 [label="7",fontsize=8]; 7 -- 11 [label="8",fontsize=8];
11 -- 16 [label="9",fontsize=8]; 7 -- 8 [label="10",fontsize=8];
11 -- 12 [label="11",fontsize=8]; 8 -- 12 [label="12",fontsize=8];
12 -- 17 [label="13",fontsize=8]; 8 -- 9 [label="",fontsize=8];
16 -- 17 [label="15",fontsize=8]; 15 -- 16 [label="16",fontsize=8];
2 -- 4 [label="17",fontsize=8]; 13 -- 14 [label="18",fontsize=8];
1 [pos="0,2!"]; 2 [pos="0.5,3.5!"];
3 [pos="1,2!"]; 4 [pos="2,3.5!"];
5 [pos="2,0!"]; 6 [pos="2,1!"];
7 [pos="2,2!"]; 8 [pos="2,3!"];
9 [pos="2,4!"]; 10 [pos="3,1!"];
11 [pos="3,2!"]; 12 [pos="3,3!"];
13 [pos="3.5,2.3!"]; 14 [pos="3.5,4!"];
15 [pos="4,1!"]; 16 [pos="4,2!"];
17 [pos="4,3!"];
}](_images/graphviz-0efc1c6f9c1a1176ac42aaa8de0be1e9186f8539.png)
The answer to that question will depend on the application.
Is there such a small curb:
That does not allow a vehicle to use that visual intersection?
Is the application for pedestrians and therefore the pedestrian can easily walk on the small curb?
Is the application for the electricity and the electrical lines than can easily be extended on top of the small curb?
Is there a big cliff and from eagles view look like the dead end is close to the segment?
Depending on the answer, modification of the data might be needed.
When there are many dead ends, to speed up processing, the Contraction - Family of functions functions can be used to contract the graph.
Linear edges¶
To get the linear edges:
SELECT id FROM vertices
WHERE array_length(in_edges || out_edges, 1) = 2;
id
----
3
9
13
15
16
(5 rows)
![graph G {
3,15,17 [shape=circle;style=filled;color=lightgreen;fontsize=8;width=0.3;fixedsize=true];
1,2,4,5,6,7,8,9,10,11,12,13,14,16 [shape=circle;style=filled;color=cyan;fontsize=8;width=0.3;fixedsize=true];
5 -- 6 [label="1",fontsize=8]; 6 -- 10 [label="2",fontsize=8];
10 -- 15 [label="3",fontsize=8]; 6 -- 7 [label="4",fontsize=8];
10 -- 11 [label="5",fontsize=8]; 1 -- 3 [label="6",fontsize=8];
3 -- 7 [label="7",fontsize=8]; 7 -- 11 [label="8",fontsize=8];
11 -- 16 [label="9",fontsize=8]; 7 -- 8 [label="10",fontsize=8];
11 -- 12 [label="11",fontsize=8]; 8 -- 12 [label="12",fontsize=8];
12 -- 17 [label="13",fontsize=8]; 8 -- 9 [label="",fontsize=8];
16 -- 17 [label="15",fontsize=8]; 15 -- 16 [label="16",fontsize=8];
2 -- 4 [label="17",fontsize=8]; 13 -- 14 [label="18",fontsize=8];
1 [pos="0,2!"]; 2 [pos="0.5,3.5!"];
3 [pos="1,2!"]; 4 [pos="2,3.5!"];
5 [pos="2,0!"]; 6 [pos="2,1!"];
7 [pos="2,2!"]; 8 [pos="2,3!"];
9 [pos="2,4!"]; 10 [pos="3,1!"];
11 [pos="3,2!"]; 12 [pos="3,3!"];
13 [pos="3.5,2.3!"]; 14 [pos="3.5,4!"];
15 [pos="4,1!"]; 16 [pos="4,2!"];
17 [pos="4,3!"];
}](_images/graphviz-fcaa0541303f92371c3cf508089a4be8712de558.png)
These linear vertices are correct, for example, when those the vertices are speed bumps, stop signals and the application is taking them into account.
When there are many linear vertices, that need not to be taken into account, to speed up the processing, the Contraction - Family of functions functions can be used to contract the problem.
Function’s structure¶
Once the graph preparation work has been done above, it is time to use a
The general form of a pgRouting function call is:
pgr_<name>(Inner queries, parameters, [ Optional parameters)
Where:
Inner queries: Are compulsory parameters that are
TEXTstrings containing SQL queries.parameters: Additional compulsory parameters needed by the function.
Optional parameters: Are non compulsory named parameters that have a default value when omitted.
The compulsory parameters are positional parameters, the optional parameters are named parameters.
For example, for this pgr_dijkstra signature:
pgr_dijkstra(Edges SQL, start vids, end vids, [directed])
-
Is the first parameter.
It is compulsory.
It is an inner query.
It has no name, so Edges SQL gives an idea of what kind of inner query needs to be used
start vid:
Is the second parameter.
It is compulsory.
It has no name, so start vid gives an idea of what the second parameter’s value should contain.
end vid
Is the third parameter.
It is compulsory.
It has no name, so end vid gives an idea of what the third parameter’s value should contain
directedIs the fourth parameter.
It is optional.
It has a name.
The full description of the parameters are found on the Parameters section of each function.
Function’s overloads¶
A function might have different overloads. The most common are called:
Depending on the overload the parameters types change.
One: ANY-INTEGER
Many:
ARRAY[ANY-INTEGER]
Depending of the function the overloads may vary. But the concept of parameter type change remains the same.
One to One¶
When routing from:
From one starting vertex
to one ending vertex
One to Many¶
When routing from:
From one starting vertex
to many ending vertices
Many to One¶
When routing from:
From many starting vertices
to one ending vertex
Many to Many¶
When routing from:
From many starting vertices
to many ending vertices
Combinations¶
When routing from:
From many different starting vertices
to many different ending vertices
Every tuple specifies a pair of a start vertex and an end vertex
Users can define the combinations as desired.
Needs a Combinations SQL
Inner Queries¶
There are several kinds of valid inner queries and also the columns returned are depending of the function. Which kind of inner query will depend on the function’s requirements. To simplify the variety of types, ANY-INTEGER and ANY-NUMERICAL is used.
Where:
- ANY-INTEGER:
SMALLINT, INTEGER, BIGINT
- ANY-NUMERICAL:
SMALLINT, INTEGER, BIGINT, REAL, FLOAT
Edges SQL¶
General¶
Edges SQL for
Some uncategorised functions
Column |
Type |
Default |
Description |
|---|---|---|---|
|
ANY-INTEGER |
Identifier of the edge. |
|
|
ANY-INTEGER |
Identifier of the first end point vertex of the edge. |
|
|
ANY-INTEGER |
Identifier of the second end point vertex of the edge. |
|
|
ANY-NUMERICAL |
Weight of the edge ( |
|
|
ANY-NUMERICAL |
-1 |
Weight of the edge (
|
Where:
- ANY-INTEGER:
SMALLINT,INTEGER,BIGINT- ANY-NUMERICAL:
SMALLINT,INTEGER,BIGINT,REAL,FLOAT
General without id¶
Edges SQL for
Column |
Type |
Default |
Description |
|---|---|---|---|
|
ANY-INTEGER |
Identifier of the first end point vertex of the edge. |
|
|
ANY-INTEGER |
Identifier of the second end point vertex of the edge. |
|
|
ANY-NUMERICAL |
Weight of the edge ( |
|
|
ANY-NUMERICAL |
-1 |
Weight of the edge (
|
Where:
- ANY-INTEGER:
SMALLINT,INTEGER,BIGINT- ANY-NUMERICAL:
SMALLINT,INTEGER,BIGINT,REAL,FLOAT
General with (X,Y)¶
Edges SQL for
Parameter |
Type |
Default |
Description |
|---|---|---|---|
|
ANY-INTEGER |
Identifier of the edge. |
|
|
ANY-INTEGER |
Identifier of the first end point vertex of the edge. |
|
|
ANY-INTEGER |
Identifier of the second end point vertex of the edge. |
|
|
ANY-NUMERICAL |
Weight of the edge (
|
|
|
ANY-NUMERICAL |
-1 |
Weight of the edge (
|
|
ANY-NUMERICAL |
X coordinate of |
|
|
ANY-NUMERICAL |
Y coordinate of |
|
|
ANY-NUMERICAL |
X coordinate of |
|
|
ANY-NUMERICAL |
Y coordinate of |
Where:
- ANY-INTEGER:
SMALLINT,INTEGER,BIGINT- ANY-NUMERICAL:
SMALLINT,INTEGER,BIGINT,REAL,FLOAT
Flow¶
Edges SQL for Flow - Family of functions
Edges SQL for
Column |
Type |
Default |
Description |
|---|---|---|---|
|
ANY-INTEGER |
Identifier of the edge. |
|
|
ANY-INTEGER |
Identifier of the first end point vertex of the edge. |
|
|
ANY-INTEGER |
Identifier of the second end point vertex of the edge. |
|
|
ANY-INTEGER |
Weight of the edge ( |
|
|
ANY-INTEGER |
-1 |
Weight of the edge (
|
Where:
- ANY-INTEGER:
SMALLINT,INTEGER,BIGINT- ANY-NUMERICAL:
SMALLINT,INTEGER,BIGINT,REAL,FLOAT
Edges SQL for the following functions of Flow - Family of functions
Column |
Type |
Default |
Description |
|---|---|---|---|
|
ANY-INTEGER |
Identifier of the edge. |
|
|
ANY-INTEGER |
Identifier of the first end point vertex of the edge. |
|
|
ANY-INTEGER |
Identifier of the second end point vertex of the edge. |
|
|
ANY-INTEGER |
Capacity of the edge (
|
|
|
ANY-INTEGER |
-1 |
Capacity of the edge (
|
|
ANY-NUMERICAL |
Weight of the edge ( |
|
|
ANY-NUMERICAL |
Weight of the edge ( |
Where:
- ANY-INTEGER:
SMALLINT,INTEGER,BIGINT- ANY-NUMERICAL:
SMALLINT,INTEGER,BIGINT,REAL,FLOAT
Combinations SQL¶
Used in combination signatures
Parameter |
Type |
Description |
|---|---|---|
|
ANY-INTEGER |
Identifier of the departure vertex. |
|
ANY-INTEGER |
Identifier of the arrival vertex. |
Where:
- ANY-INTEGER:
SMALLINT,INTEGER,BIGINT
Restrictions SQL¶
Column |
Type |
Description |
|---|---|---|
|
|
Sequence of edge identifiers that form a path that is not allowed to be
taken.
- Empty arrays or |
|
ANY-NUMERICAL |
Cost of taking the forbidden path. |
Where:
- ANY-INTEGER:
SMALLINT,INTEGER,BIGINT- ANY-NUMERICAL:
SMALLINT,INTEGER,BIGINT,REAL,FLOAT
Points SQL¶
Points SQL for
Parameter |
Type |
Default |
Description |
|---|---|---|---|
|
ANY-INTEGER |
value |
Identifier of the point.
|
|
ANY-INTEGER |
Identifier of the “closest” edge to the point. |
|
|
ANY-NUMERICAL |
Value in <0,1> that indicates the relative postition from the first end point of the edge. |
|
|
|
|
Value in [
|
Where:
- ANY-INTEGER:
SMALLINT,INTEGER,BIGINT- ANY-NUMERICAL:
SMALLINT,INTEGER,BIGINT,REAL,FLOAT
Parameters¶
The main parameter of the majority of the pgRouting functions is a query that selects the edges of the graph.
Parameter |
Type |
Description |
|---|---|---|
|
Edges SQL as described below. |
Depending on the family or category of a function it will have additional parameters, some of them are compulsory and some are optional.
The compulsory parameters are nameless and must be given in the required order. The optional parameters are named parameters and will have a default value.
Parameters for the Via functions¶
Parameter |
Type |
Default |
Description |
|---|---|---|---|
|
SQL query as described. |
||
via vertices |
|
Array of ordered vertices identifiers that are going to be visited. |
|
|
|
|
|
|
|
|
|
|
|
|
|
For the TRSP functions¶
Column |
Type |
Description |
|---|---|---|
|
SQL query as described. |
|
|
SQL query as described. |
|
|
Combinations SQL as described below |
|
start vid |
ANY-INTEGER |
Identifier of the departure vertex. |
start vids |
|
Array of identifiers of destination vertices. |
end vid |
ANY-INTEGER |
Identifier of the departure vertex. |
end vids |
|
Array of identifiers of destination vertices. |
Where:
- ANY-INTEGER:
SMALLINT,INTEGER,BIGINT
Result columns¶
There are several kinds of columns returned are depending of the function.
Result columns for a path¶
Used in functions that return one path solution
Returns set of (seq, path_seq [, start_vid] [, end_vid], node, edge, cost,
agg_cost)
Column |
Type |
Description |
|---|---|---|
|
|
Sequential value starting from 1. |
|
|
Relative position in the path. Has value 1 for the beginning of a path. |
|
|
Identifier of the starting vertex. Returned when multiple starting vetrices are in the query. |
|
|
Identifier of the ending vertex. Returned when multiple ending vertices are in the query. |
|
|
Identifier of the node in the path from |
|
|
Identifier of the edge used to go from |
|
|
Cost to traverse from |
|
|
Aggregate cost from |
Used in functions the following:
Returns set of (seq, path_seq [, start_pid] [, end_pid], node, edge, cost,
agg_cost)
Column |
Type |
Description |
|---|---|---|
|
|
Sequential value starting from 1. |
|
|
Relative position in the path.
|
|
|
Identifier of a starting vertex/point of the path.
|
|
|
Identifier of an ending vertex/point of the path.
|
|
|
Identifier of the node in the path from
|
|
|
Identifier of the edge used to go from
|
|
|
Cost to traverse from
|
|
|
Aggregate cost from
|
Used in functions the following:
Returns (seq, path_seq, start_vid, end_vid, node, edge, cost, agg_cost)
Column |
Type |
Description |
|---|---|---|
|
|
Sequential value starting from 1. |
|
|
Relative position in the path. Has value 1 for the beginning of a path. |
|
|
Identifier of the starting vertex of the current path. |
|
|
Identifier of the ending vertex of the current path. |
|
|
Identifier of the node in the path from |
|
|
Identifier of the edge used to go from |
|
|
Cost to traverse from |
|
|
Aggregate cost from |
Multiple paths¶
Selective for multiple paths.¶
The columns depend on the function call.
Set of (seq, path_id, path_seq [, start_vid] [, end_vid], node, edge, cost,
agg_cost)
Column |
Type |
Description |
|---|---|---|
|
|
Sequential value starting from 1. |
|
|
Path identifier.
|
|
|
Relative position in the path. Has value 1 for the beginning of a path. |
|
|
Identifier of the starting vertex. Returned when multiple starting vetrices are in the query. |
|
|
Identifier of the ending vertex. Returned when multiple ending vertices are in the query. |
|
|
Identifier of the node in the path from |
|
|
Identifier of the edge used to go from |
|
|
Cost to traverse from |
|
|
Aggregate cost from |
Non selective for multiple paths¶
Regardless of the call, al the columns are returned.
Returns set of (seq, path_id, path_seq, start_vid, end_vid, node, edge, cost,
agg_cost)
Column |
Type |
Description |
|---|---|---|
|
|
Sequential value starting from 1. |
|
|
Path identifier.
|
|
|
Relative position in the path. Has value 1 for the beginning of a path. |
|
|
Identifier of the starting vertex. |
|
|
Identifier of the ending vertex. |
|
|
Identifier of the node in the path from |
|
|
Identifier of the edge used to go from |
|
|
Cost to traverse from |
|
|
Aggregate cost from |
Result columns for cost functions¶
Used in the following
Set of (start_vid, end_vid, agg_cost)
Column |
Type |
Description |
|---|---|---|
|
|
Identifier of the starting vertex. |
|
|
Identifier of the ending vertex. |
|
|
Aggregate cost from |
Note
When start_vid or end_vid columns have negative values, the identifier is for a Point.
Result columns for flow functions¶
Edges SQL for the following
Column |
Type |
Description |
|---|---|---|
seq |
|
Sequential value starting from 1. |
edge |
|
Identifier of the edge in the original query (edges_sql). |
start_vid |
|
Identifier of the first end point vertex of the edge. |
end_vid |
|
Identifier of the second end point vertex of the edge. |
flow |
|
Flow through the edge in the direction
( |
residual_capacity |
|
Residual capacity of the edge in the direction
( |
Edges SQL for the following functions of Flow - Family of functions
Column |
Type |
Description |
|---|---|---|
seq |
|
Sequential value starting from 1. |
edge |
|
Identifier of the edge in the original query (edges_sql). |
source |
|
Identifier of the first end point vertex of the edge. |
target |
|
Identifier of the second end point vertex of the edge. |
flow |
|
Flow through the edge in the direction (source, target). |
residual_capacity |
|
Residual capacity of the edge in the direction (source, target). |
cost |
|
The cost of sending this flow through the edge in the direction (source, target). |
agg_cost |
|
The aggregate cost. |
Result columns for spanning tree functions¶
Edges SQL for the following
Returns set of (edge, cost)
Column |
Type |
Description |
|---|---|---|
|
|
Identifier of the edge. |
|
|
Cost to traverse the edge. |
Performance Tips¶
For the Routing functions¶
To get faster results bound the queries to an area of interest of routing.
In this example Use an inner query SQL that does not include some edges in the routing function and is within the area of the results.
Given this area:
SELECT id, source, target, cost, reverse_cost
FROM edges
WHERE geom && (
SELECT st_buffer(geom, 1) as myarea
FROM edges where id = 6) ORDER BY id;
id | source | target | cost | reverse_cost
----+--------+--------+------+--------------
1 | 5 | 6 | 1 | 1
2 | 6 | 10 | -1 | 1
4 | 6 | 7 | 1 | 1
6 | 1 | 3 | 1 | 1
7 | 3 | 7 | 1 | 1
8 | 7 | 11 | 1 | 1
10 | 7 | 8 | 1 | 1
12 | 8 | 12 | 1 | -1
14 | 8 | 9 | 1 | 1
20 | 8 | 4 | 0.5 | 0.5
(10 rows)
Calculate a route:
SELECT * FROM pgr_dijkstra($$
SELECT id, source, target, cost, reverse_cost
FROM edges
WHERE geom && (
SELECT st_buffer(geom, 1) AS myarea
FROM edges WHERE id = 6)$$,
7, 8);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 7 | 8 | 7 | 10 | 1 | 0
2 | 2 | 7 | 8 | 8 | -1 | 0 | 1
(2 rows)
How to contribute¶
Wiki
Edit an existing pgRouting Wiki page.
Or create a new Wiki page
Create a page on the pgRouting Wiki
Give the title an appropriate name
Adding Functionality to pgRouting
Consult the developer’s documentation
Indices and tables