pgr_dijkstra¶
pgr_dijkstra — Shortest path using Dijkstra algorithm.
Boost Graph Inside¶
Availability
Version 3.5.0
Standarizing output columns to
(seq, path_seq, start_vid, end_vid, node, edge, cost, agg_cost)pgr_dijkstra(One to One) addedstart_vidandend_vidcolumns.pgr_dijkstra(One to Many) addedend_vidcolumn.pgr_dijkstra(Many to One) addedstart_vidcolumn.
Version 3.1.0
New Proposed functions:
pgr_dijkstra(Combinations)
Version 3.0.0
Official functions
Version 2.2.0
New proposed functions:
pgr_dijkstra(One to Many)pgr_dijkstra(Many to One)pgr_dijkstra(Many to Many)
Version 2.1.0
Signature change on
pgr_dijkstra(One to One)
Version 2.0.0
Official
pgr_dijkstra(One to One)
Description¶
Dijkstra’s algorithm, conceived by Dutch computer scientist Edsger Dijkstra in 1956. It is a graph search algorithm that solves the shortest path problem for a graph with non-negative edge path costs, producing a shortest path from a starting vertex to an ending vertex. This implementation can be used with a directed graph and an undirected graph.
Process is done only on edges with positive costs.
A negative value on a cost column is interpreted as the edge does not exist.
Values are returned when there is a path.
When there is no path:
When the starting vertex and ending vertex are the same.
The aggregate cost of the non included values \((v, v)\) is \(0\)
When the starting vertex and ending vertex are the different and there is no path:
The aggregate cost the non included values \((u, v)\) is \(\infty\)
For optimization purposes, any duplicated value in the starting vertices or on the ending vertices are ignored.
Running time: \(O(| start\ vids | * (V \log V + E))\)
Signatures¶
Summary
pgr_dijkstra(Edges SQL, start vid, end vid, [
directed])pgr_dijkstra(Edges SQL, start vid, end vids, [
directed])pgr_dijkstra(Edges SQL, start vids, end vid, [
directed])pgr_dijkstra(Edges SQL, start vids, end vids, [
directed])Returns set of
(seq, path_seq, start_vid, end_vid, node, edge, cost, agg_cost)OR EMPTY SET
Warning
Breaking change on 3.5.0
Read the Migration guide about how to migrate from the old result columns to the new result columns.
One to One¶
pgr_dijkstra(Edges SQL, start vid, end vid, [
directed])Returns set of
(seq, path_seq, start_vid, end_vid, node, edge, cost, agg_cost)OR EMPTY SET
- Example:
From vertex \(6\) to vertex \(10\) on a directed graph
SELECT * FROM pgr_Dijkstra(
'select id, source, target, cost, reverse_cost from edges',
6, 10, true);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 10 | 6 | 4 | 1 | 0
2 | 2 | 6 | 10 | 7 | 8 | 1 | 1
3 | 3 | 6 | 10 | 11 | 9 | 1 | 2
4 | 4 | 6 | 10 | 16 | 16 | 1 | 3
5 | 5 | 6 | 10 | 15 | 3 | 1 | 4
6 | 6 | 6 | 10 | 10 | -1 | 0 | 5
(6 rows)
One to Many¶
pgr_dijkstra(Edges SQL, start vid, end vids, [
directed])Returns set of
(seq, path_seq, start_vid, end_vid, node, edge, cost, agg_cost)OR EMPTY SET
- Example:
From vertex \(6\) to vertices \(\{10, 17\}\) on a directed
SELECT * FROM pgr_Dijkstra(
'select id, source, target, cost, reverse_cost from edges',
6, ARRAY[10, 17]);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 10 | 6 | 4 | 1 | 0
2 | 2 | 6 | 10 | 7 | 8 | 1 | 1
3 | 3 | 6 | 10 | 11 | 9 | 1 | 2
4 | 4 | 6 | 10 | 16 | 16 | 1 | 3
5 | 5 | 6 | 10 | 15 | 3 | 1 | 4
6 | 6 | 6 | 10 | 10 | -1 | 0 | 5
7 | 1 | 6 | 17 | 6 | 4 | 1 | 0
8 | 2 | 6 | 17 | 7 | 8 | 1 | 1
9 | 3 | 6 | 17 | 11 | 9 | 1 | 2
10 | 4 | 6 | 17 | 16 | 15 | 1 | 3
11 | 5 | 6 | 17 | 17 | -1 | 0 | 4
(11 rows)
Many to One¶
pgr_dijkstra(Edges SQL, start vids, end vid, [
directed])Returns set of
(seq, path_seq, start_vid, end_vid, node, edge, cost, agg_cost)OR EMPTY SET
- Example:
From vertices \(\{6, 1\}\) to vertex \(17\) on a directed graph
SELECT * FROM pgr_Dijkstra(
'select id, source, target, cost, reverse_cost from edges',
ARRAY[6, 1], 17);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 1 | 17 | 1 | 6 | 1 | 0
2 | 2 | 1 | 17 | 3 | 7 | 1 | 1
3 | 3 | 1 | 17 | 7 | 8 | 1 | 2
4 | 4 | 1 | 17 | 11 | 11 | 1 | 3
5 | 5 | 1 | 17 | 12 | 13 | 1 | 4
6 | 6 | 1 | 17 | 17 | -1 | 0 | 5
7 | 1 | 6 | 17 | 6 | 4 | 1 | 0
8 | 2 | 6 | 17 | 7 | 8 | 1 | 1
9 | 3 | 6 | 17 | 11 | 11 | 1 | 2
10 | 4 | 6 | 17 | 12 | 13 | 1 | 3
11 | 5 | 6 | 17 | 17 | -1 | 0 | 4
(11 rows)
Many to Many¶
pgr_dijkstra(Edges SQL, start vids, end vids, [
directed])Returns set of
(seq, path_seq, start_vid, end_vid, node, edge, cost, agg_cost)OR EMPTY SET
- Example:
From vertices \(\{6, 1\}\) to vertices \(\{10, 17\}\) on an undirected graph
SELECT * FROM pgr_Dijkstra(
'select id, source, target, cost, reverse_cost from edges',
ARRAY[6, 1], ARRAY[10, 17],
directed => false);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 1 | 10 | 1 | 6 | 1 | 0
2 | 2 | 1 | 10 | 3 | 7 | 1 | 1
3 | 3 | 1 | 10 | 7 | 4 | 1 | 2
4 | 4 | 1 | 10 | 6 | 2 | 1 | 3
5 | 5 | 1 | 10 | 10 | -1 | 0 | 4
6 | 1 | 1 | 17 | 1 | 6 | 1 | 0
7 | 2 | 1 | 17 | 3 | 7 | 1 | 1
8 | 3 | 1 | 17 | 7 | 8 | 1 | 2
9 | 4 | 1 | 17 | 11 | 9 | 1 | 3
10 | 5 | 1 | 17 | 16 | 15 | 1 | 4
11 | 6 | 1 | 17 | 17 | -1 | 0 | 5
12 | 1 | 6 | 10 | 6 | 2 | 1 | 0
13 | 2 | 6 | 10 | 10 | -1 | 0 | 1
14 | 1 | 6 | 17 | 6 | 4 | 1 | 0
15 | 2 | 6 | 17 | 7 | 8 | 1 | 1
16 | 3 | 6 | 17 | 11 | 11 | 1 | 2
17 | 4 | 6 | 17 | 12 | 13 | 1 | 3
18 | 5 | 6 | 17 | 17 | -1 | 0 | 4
(18 rows)
Combinations¶
Returns set of
(seq, path_seq, start_vid, end_vid, node, edge, cost, agg_cost)OR EMPTY SET
- Example:
Using a combinations table on an undirected graph
The combinations table:
SELECT source, target FROM combinations;
source | target
--------+--------
5 | 6
5 | 10
6 | 5
6 | 15
6 | 14
(5 rows)
The query:
SELECT * FROM pgr_Dijkstra(
'SELECT id, source, target, cost, reverse_cost FROM edges',
'SELECT source, target FROM combinations',
false);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 5 | 6 | 5 | 1 | 1 | 0
2 | 2 | 5 | 6 | 6 | -1 | 0 | 1
3 | 1 | 5 | 10 | 5 | 1 | 1 | 0
4 | 2 | 5 | 10 | 6 | 2 | 1 | 1
5 | 3 | 5 | 10 | 10 | -1 | 0 | 2
6 | 1 | 6 | 5 | 6 | 1 | 1 | 0
7 | 2 | 6 | 5 | 5 | -1 | 0 | 1
8 | 1 | 6 | 15 | 6 | 2 | 1 | 0
9 | 2 | 6 | 15 | 10 | 3 | 1 | 1
10 | 3 | 6 | 15 | 15 | -1 | 0 | 2
(10 rows)
Parameters¶
Column |
Type |
Description |
|---|---|---|
|
Edges SQL as described below |
|
|
Combinations SQL as described below |
|
start vid |
|
Identifier of the starting vertex of the path. |
start vids |
|
Array of identifiers of starting vertices. |
end vid |
|
Identifier of the ending vertex of the path. |
end vids |
|
Array of identifiers of ending vertices. |
Optional parameters¶
Column |
Type |
Default |
Description |
|---|---|---|---|
|
|
|
|
Inner Queries¶
Edges SQL¶
Column |
Type |
Default |
Description |
|---|---|---|---|
|
ANY-INTEGER |
Identifier of the edge. |
|
|
ANY-INTEGER |
Identifier of the first end point vertex of the edge. |
|
|
ANY-INTEGER |
Identifier of the second end point vertex of the edge. |
|
|
ANY-NUMERICAL |
Weight of the edge ( |
|
|
ANY-NUMERICAL |
-1 |
Weight of the edge (
|
Where:
- ANY-INTEGER:
SMALLINT,INTEGER,BIGINT- ANY-NUMERICAL:
SMALLINT,INTEGER,BIGINT,REAL,FLOAT
Combinations SQL¶
Parameter |
Type |
Description |
|---|---|---|
|
ANY-INTEGER |
Identifier of the departure vertex. |
|
ANY-INTEGER |
Identifier of the arrival vertex. |
Where:
- ANY-INTEGER:
SMALLINT,INTEGER,BIGINT
Result columns¶
Returns set of (seq, path_seq [, start_vid] [, end_vid], node, edge, cost,
agg_cost)
Column |
Type |
Description |
|---|---|---|
|
|
Sequential value starting from 1. |
|
|
Relative position in the path. Has value 1 for the beginning of a path. |
|
|
Identifier of the starting vertex. Returned when multiple starting vetrices are in the query. |
|
|
Identifier of the ending vertex. Returned when multiple ending vertices are in the query. |
|
|
Identifier of the node in the path from |
|
|
Identifier of the edge used to go from |
|
|
Cost to traverse from |
|
|
Aggregate cost from |
Additional Examples¶
- Example:
Demonstration of repeated values are ignored, and result is sorted.
SELECT * FROM pgr_Dijkstra(
'select id, source, target, cost, reverse_cost from edges',
ARRAY[7, 10, 15, 10, 10, 15], ARRAY[10, 7, 10, 15]);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 7 | 10 | 7 | 8 | 1 | 0
2 | 2 | 7 | 10 | 11 | 9 | 1 | 1
3 | 3 | 7 | 10 | 16 | 16 | 1 | 2
4 | 4 | 7 | 10 | 15 | 3 | 1 | 3
5 | 5 | 7 | 10 | 10 | -1 | 0 | 4
6 | 1 | 7 | 15 | 7 | 8 | 1 | 0
7 | 2 | 7 | 15 | 11 | 9 | 1 | 1
8 | 3 | 7 | 15 | 16 | 16 | 1 | 2
9 | 4 | 7 | 15 | 15 | -1 | 0 | 3
10 | 1 | 10 | 7 | 10 | 5 | 1 | 0
11 | 2 | 10 | 7 | 11 | 8 | 1 | 1
12 | 3 | 10 | 7 | 7 | -1 | 0 | 2
13 | 1 | 10 | 15 | 10 | 5 | 1 | 0
14 | 2 | 10 | 15 | 11 | 9 | 1 | 1
15 | 3 | 10 | 15 | 16 | 16 | 1 | 2
16 | 4 | 10 | 15 | 15 | -1 | 0 | 3
17 | 1 | 15 | 7 | 15 | 16 | 1 | 0
18 | 2 | 15 | 7 | 16 | 9 | 1 | 1
19 | 3 | 15 | 7 | 11 | 8 | 1 | 2
20 | 4 | 15 | 7 | 7 | -1 | 0 | 3
21 | 1 | 15 | 10 | 15 | 3 | 1 | 0
22 | 2 | 15 | 10 | 10 | -1 | 0 | 1
(22 rows)
- Example 2:
Making start_vids the same as end_vids
SELECT * FROM pgr_Dijkstra(
'select id, source, target, cost, reverse_cost from edges',
ARRAY[7, 10, 15], ARRAY[7, 10, 15]);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 7 | 10 | 7 | 8 | 1 | 0
2 | 2 | 7 | 10 | 11 | 9 | 1 | 1
3 | 3 | 7 | 10 | 16 | 16 | 1 | 2
4 | 4 | 7 | 10 | 15 | 3 | 1 | 3
5 | 5 | 7 | 10 | 10 | -1 | 0 | 4
6 | 1 | 7 | 15 | 7 | 8 | 1 | 0
7 | 2 | 7 | 15 | 11 | 9 | 1 | 1
8 | 3 | 7 | 15 | 16 | 16 | 1 | 2
9 | 4 | 7 | 15 | 15 | -1 | 0 | 3
10 | 1 | 10 | 7 | 10 | 5 | 1 | 0
11 | 2 | 10 | 7 | 11 | 8 | 1 | 1
12 | 3 | 10 | 7 | 7 | -1 | 0 | 2
13 | 1 | 10 | 15 | 10 | 5 | 1 | 0
14 | 2 | 10 | 15 | 11 | 9 | 1 | 1
15 | 3 | 10 | 15 | 16 | 16 | 1 | 2
16 | 4 | 10 | 15 | 15 | -1 | 0 | 3
17 | 1 | 15 | 7 | 15 | 16 | 1 | 0
18 | 2 | 15 | 7 | 16 | 9 | 1 | 1
19 | 3 | 15 | 7 | 11 | 8 | 1 | 2
20 | 4 | 15 | 7 | 7 | -1 | 0 | 3
21 | 1 | 15 | 10 | 15 | 3 | 1 | 0
22 | 2 | 15 | 10 | 10 | -1 | 0 | 1
(22 rows)
- Example:
Manually assigned vertex combinations.
SELECT * FROM pgr_Dijkstra(
'SELECT id, source, target, cost, reverse_cost FROM edges',
'SELECT * FROM (VALUES (6, 10), (6, 7), (12, 10)) AS combinations (source, target)');
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 7 | 6 | 4 | 1 | 0
2 | 2 | 6 | 7 | 7 | -1 | 0 | 1
3 | 1 | 6 | 10 | 6 | 4 | 1 | 0
4 | 2 | 6 | 10 | 7 | 8 | 1 | 1
5 | 3 | 6 | 10 | 11 | 9 | 1 | 2
6 | 4 | 6 | 10 | 16 | 16 | 1 | 3
7 | 5 | 6 | 10 | 15 | 3 | 1 | 4
8 | 6 | 6 | 10 | 10 | -1 | 0 | 5
9 | 1 | 12 | 10 | 12 | 13 | 1 | 0
10 | 2 | 12 | 10 | 17 | 15 | 1 | 1
11 | 3 | 12 | 10 | 16 | 16 | 1 | 2
12 | 4 | 12 | 10 | 15 | 3 | 1 | 3
13 | 5 | 12 | 10 | 10 | -1 | 0 | 4
(13 rows)
The examples of this section are based on the Sample Data network.
For directed graphs with cost and reverse_cost columns¶
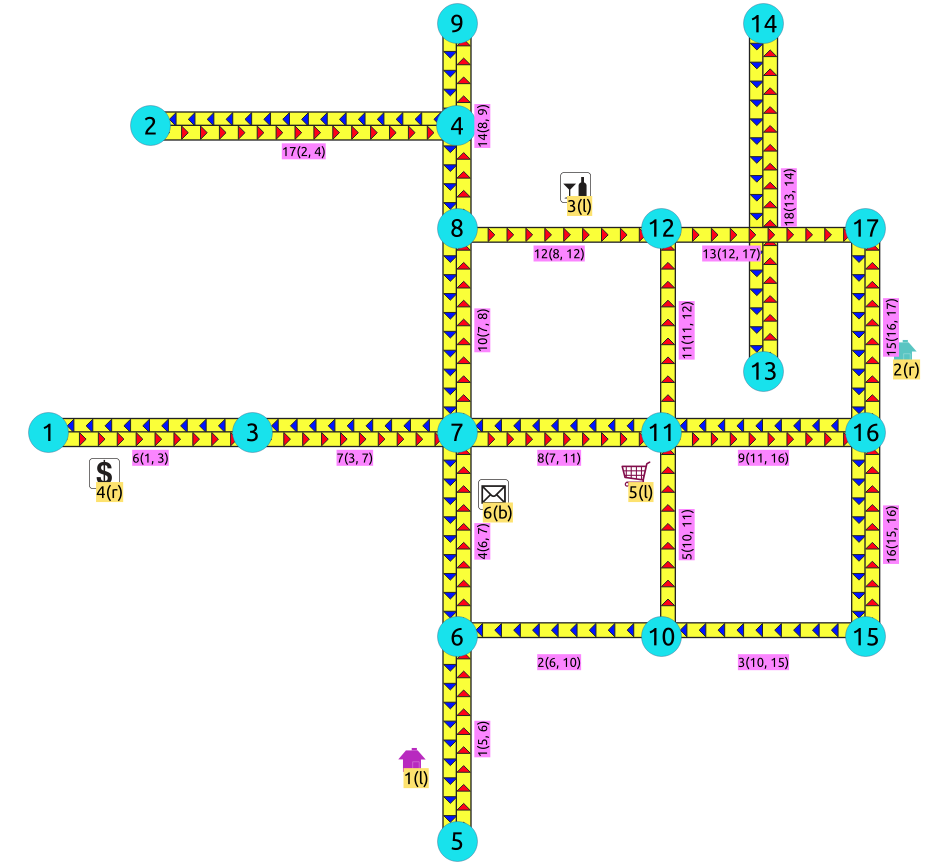
Directed graph with cost and reverse cost columns¶
1) Path from \(6\) to \(10\)¶
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost, reverse_cost FROM edges',
6, 10
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 10 | 6 | 4 | 1 | 0
2 | 2 | 6 | 10 | 7 | 8 | 1 | 1
3 | 3 | 6 | 10 | 11 | 9 | 1 | 2
4 | 4 | 6 | 10 | 16 | 16 | 1 | 3
5 | 5 | 6 | 10 | 15 | 3 | 1 | 4
6 | 6 | 6 | 10 | 10 | -1 | 0 | 5
(6 rows)
2) Path from \(6\) to \(7\)¶
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost, reverse_cost FROM edges',
6, 7
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 7 | 6 | 4 | 1 | 0
2 | 2 | 6 | 7 | 7 | -1 | 0 | 1
(2 rows)
3) Path from \(12\) to \(10\)¶
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost, reverse_cost FROM edges',
12, 10
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 12 | 10 | 12 | 13 | 1 | 0
2 | 2 | 12 | 10 | 17 | 15 | 1 | 1
3 | 3 | 12 | 10 | 16 | 16 | 1 | 2
4 | 4 | 12 | 10 | 15 | 3 | 1 | 3
5 | 5 | 12 | 10 | 10 | -1 | 0 | 4
(5 rows)
4) Path from \(12\) to \(7\)¶
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost, reverse_cost FROM edges',
12, 7
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 12 | 7 | 12 | 13 | 1 | 0
2 | 2 | 12 | 7 | 17 | 15 | 1 | 1
3 | 3 | 12 | 7 | 16 | 9 | 1 | 2
4 | 4 | 12 | 7 | 11 | 8 | 1 | 3
5 | 5 | 12 | 7 | 7 | -1 | 0 | 4
(5 rows)
5) Using One to Many to get the solution of examples 1 and 2¶
Paths \(\{6\}\rightarrow\{10, 7\}\)
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost, reverse_cost FROM edges',
6, ARRAY[10, 7]
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 7 | 6 | 4 | 1 | 0
2 | 2 | 6 | 7 | 7 | -1 | 0 | 1
3 | 1 | 6 | 10 | 6 | 4 | 1 | 0
4 | 2 | 6 | 10 | 7 | 8 | 1 | 1
5 | 3 | 6 | 10 | 11 | 9 | 1 | 2
6 | 4 | 6 | 10 | 16 | 16 | 1 | 3
7 | 5 | 6 | 10 | 15 | 3 | 1 | 4
8 | 6 | 6 | 10 | 10 | -1 | 0 | 5
(8 rows)
6) Using Many to One to get the solution of examples 2 and 4¶
Paths \(\{6, 12\}\rightarrow\{7\}\)
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost, reverse_cost FROM edges',
ARRAY[6, 12], 7
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 7 | 6 | 4 | 1 | 0
2 | 2 | 6 | 7 | 7 | -1 | 0 | 1
3 | 1 | 12 | 7 | 12 | 13 | 1 | 0
4 | 2 | 12 | 7 | 17 | 15 | 1 | 1
5 | 3 | 12 | 7 | 16 | 9 | 1 | 2
6 | 4 | 12 | 7 | 11 | 8 | 1 | 3
7 | 5 | 12 | 7 | 7 | -1 | 0 | 4
(7 rows)
7) Using Many to Many to get the solution of examples 1 to 4¶
Paths \(\{6, 12\}\rightarrow\{10, 7\}\)
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost, reverse_cost FROM edges',
ARRAY[6, 12], ARRAY[10,7]
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 7 | 6 | 4 | 1 | 0
2 | 2 | 6 | 7 | 7 | -1 | 0 | 1
3 | 1 | 6 | 10 | 6 | 4 | 1 | 0
4 | 2 | 6 | 10 | 7 | 8 | 1 | 1
5 | 3 | 6 | 10 | 11 | 9 | 1 | 2
6 | 4 | 6 | 10 | 16 | 16 | 1 | 3
7 | 5 | 6 | 10 | 15 | 3 | 1 | 4
8 | 6 | 6 | 10 | 10 | -1 | 0 | 5
9 | 1 | 12 | 7 | 12 | 13 | 1 | 0
10 | 2 | 12 | 7 | 17 | 15 | 1 | 1
11 | 3 | 12 | 7 | 16 | 9 | 1 | 2
12 | 4 | 12 | 7 | 11 | 8 | 1 | 3
13 | 5 | 12 | 7 | 7 | -1 | 0 | 4
14 | 1 | 12 | 10 | 12 | 13 | 1 | 0
15 | 2 | 12 | 10 | 17 | 15 | 1 | 1
16 | 3 | 12 | 10 | 16 | 16 | 1 | 2
17 | 4 | 12 | 10 | 15 | 3 | 1 | 3
18 | 5 | 12 | 10 | 10 | -1 | 0 | 4
(18 rows)
8) Using Combinations to get the solution of examples 1 to 3¶
Paths \(\{6\}\rightarrow\{10, 7\}\cup\{12\}\rightarrow\{10\}\)
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost, reverse_cost FROM edges',
'SELECT * FROM (VALUES (6, 10), (6, 7), (12, 10)) AS combinations (source, target)'
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 7 | 6 | 4 | 1 | 0
2 | 2 | 6 | 7 | 7 | -1 | 0 | 1
3 | 1 | 6 | 10 | 6 | 4 | 1 | 0
4 | 2 | 6 | 10 | 7 | 8 | 1 | 1
5 | 3 | 6 | 10 | 11 | 9 | 1 | 2
6 | 4 | 6 | 10 | 16 | 16 | 1 | 3
7 | 5 | 6 | 10 | 15 | 3 | 1 | 4
8 | 6 | 6 | 10 | 10 | -1 | 0 | 5
9 | 1 | 12 | 10 | 12 | 13 | 1 | 0
10 | 2 | 12 | 10 | 17 | 15 | 1 | 1
11 | 3 | 12 | 10 | 16 | 16 | 1 | 2
12 | 4 | 12 | 10 | 15 | 3 | 1 | 3
13 | 5 | 12 | 10 | 10 | -1 | 0 | 4
(13 rows)
For undirected graphs with cost and reverse_cost columns¶
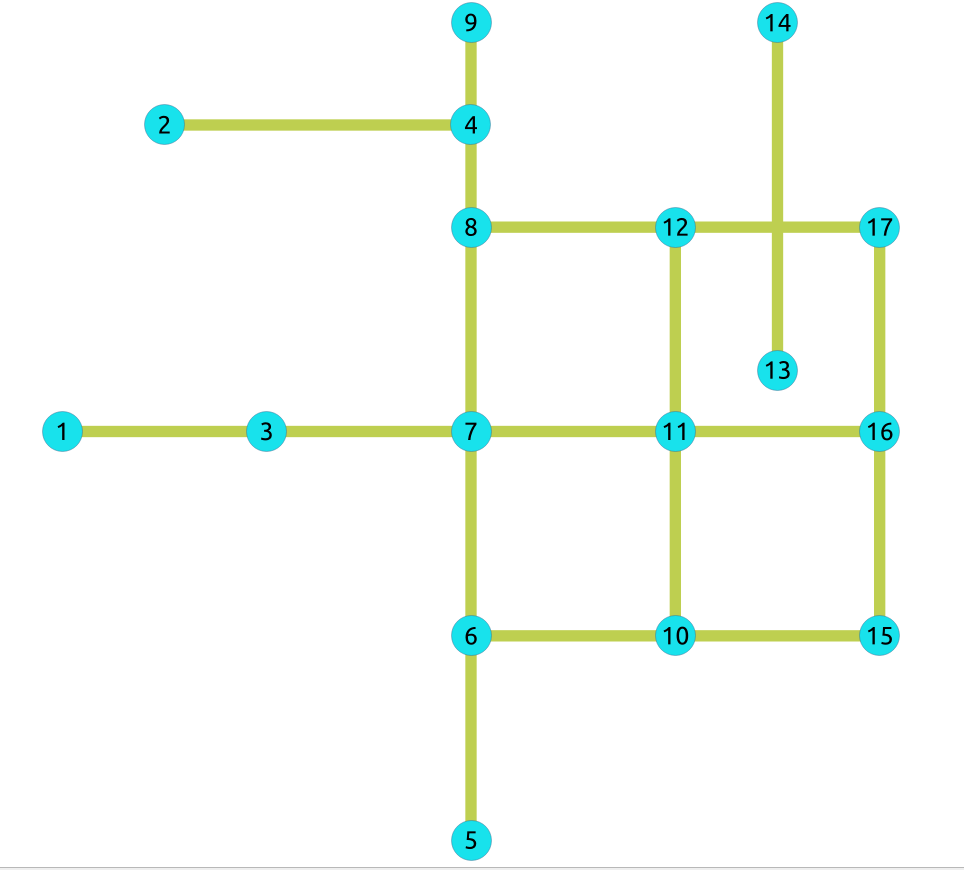
Undirected graph with cost and reverse cost columns¶
9) Path from \(6\) to \(10\)¶
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost, reverse_cost FROM edges',
6, 10,
false
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 10 | 6 | 2 | 1 | 0
2 | 2 | 6 | 10 | 10 | -1 | 0 | 1
(2 rows)
10) Path from \(6\) to \(7\)¶
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost, reverse_cost FROM edges',
6, 7,
false
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 7 | 6 | 4 | 1 | 0
2 | 2 | 6 | 7 | 7 | -1 | 0 | 1
(2 rows)
11) Path from \(12\) to \(10\)¶
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost, reverse_cost FROM edges',
12, 10,
false
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 12 | 10 | 12 | 11 | 1 | 0
2 | 2 | 12 | 10 | 11 | 5 | 1 | 1
3 | 3 | 12 | 10 | 10 | -1 | 0 | 2
(3 rows)
12) Path from \(12\) to \(7\)¶
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost, reverse_cost FROM edges',
12, 7,
false
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 12 | 7 | 12 | 12 | 1 | 0
2 | 2 | 12 | 7 | 8 | 10 | 1 | 1
3 | 3 | 12 | 7 | 7 | -1 | 0 | 2
(3 rows)
13) Using One to Many to get the solution of examples 9 and 10¶
Paths \(\{6\}\rightarrow\{10, 7\}\)
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost, reverse_cost FROM edges',
6, ARRAY[10,7],
false
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 7 | 6 | 4 | 1 | 0
2 | 2 | 6 | 7 | 7 | -1 | 0 | 1
3 | 1 | 6 | 10 | 6 | 2 | 1 | 0
4 | 2 | 6 | 10 | 10 | -1 | 0 | 1
(4 rows)
14) Using Many to One to get the solution of examples 10 and 12¶
Paths \(\{6, 12\}\rightarrow\{7\}\)
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost, reverse_cost FROM edges',
ARRAY[6,12], 7,
false
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 7 | 6 | 4 | 1 | 0
2 | 2 | 6 | 7 | 7 | -1 | 0 | 1
3 | 1 | 12 | 7 | 12 | 12 | 1 | 0
4 | 2 | 12 | 7 | 8 | 10 | 1 | 1
5 | 3 | 12 | 7 | 7 | -1 | 0 | 2
(5 rows)
15) Using Many to Many to get the solution of examples 9 to 12¶
Paths \(\{6, 12\}\rightarrow\{10, 7\}\)
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost, reverse_cost FROM edges',
ARRAY[6, 12], ARRAY[10,7],
false
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 7 | 6 | 4 | 1 | 0
2 | 2 | 6 | 7 | 7 | -1 | 0 | 1
3 | 1 | 6 | 10 | 6 | 2 | 1 | 0
4 | 2 | 6 | 10 | 10 | -1 | 0 | 1
5 | 1 | 12 | 7 | 12 | 12 | 1 | 0
6 | 2 | 12 | 7 | 8 | 10 | 1 | 1
7 | 3 | 12 | 7 | 7 | -1 | 0 | 2
8 | 1 | 12 | 10 | 12 | 11 | 1 | 0
9 | 2 | 12 | 10 | 11 | 5 | 1 | 1
10 | 3 | 12 | 10 | 10 | -1 | 0 | 2
(10 rows)
16) Using Combinations to get the solution of examples 9 to 11¶
Paths \(\{6\}\rightarrow\{10, 7\}\cup\{12\}\rightarrow\{10\}\)
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost, reverse_cost FROM edges',
'SELECT * FROM (VALUES (6, 10), (6, 7), (12, 10)) AS combinations (source, target)',
false
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 7 | 6 | 4 | 1 | 0
2 | 2 | 6 | 7 | 7 | -1 | 0 | 1
3 | 1 | 6 | 10 | 6 | 2 | 1 | 0
4 | 2 | 6 | 10 | 10 | -1 | 0 | 1
5 | 1 | 12 | 10 | 12 | 11 | 1 | 0
6 | 2 | 12 | 10 | 11 | 5 | 1 | 1
7 | 3 | 12 | 10 | 10 | -1 | 0 | 2
(7 rows)
For directed graphs only with cost column¶
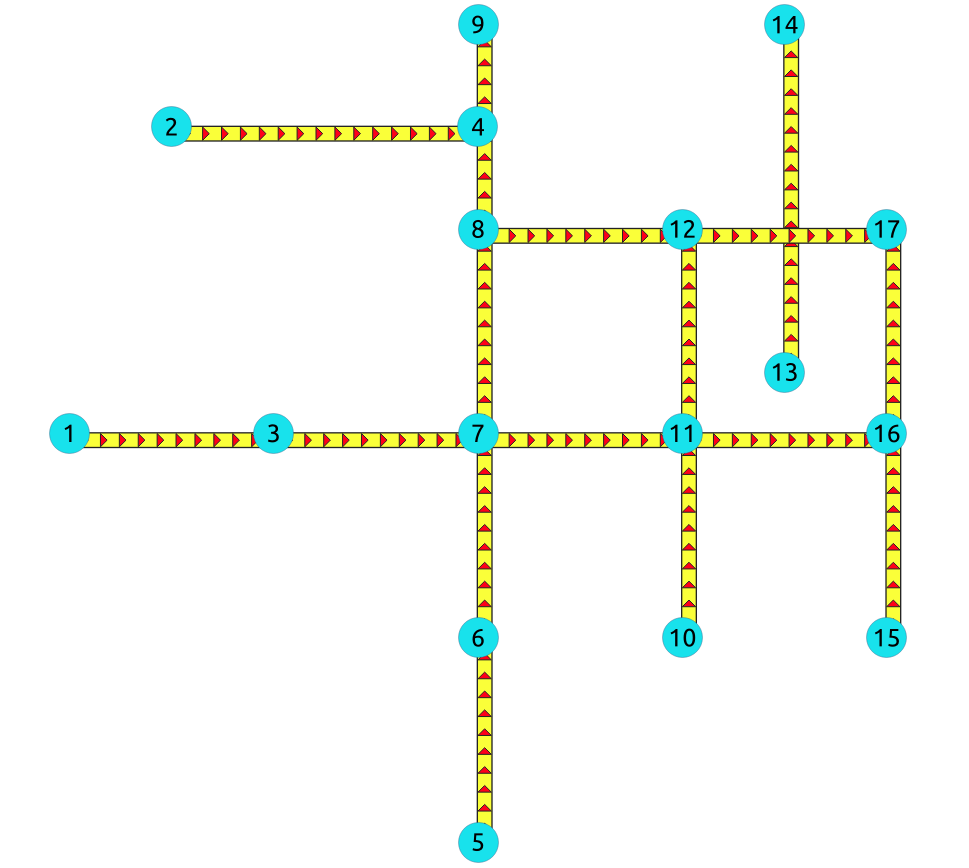
Directed graph only with cost column¶
17) Path from \(6\) to \(10\)¶
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost FROM edges',
6, 10
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
(0 rows)
18) Path from \(6\) to \(7\)¶
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost FROM edges',
6, 7
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 7 | 6 | 4 | 1 | 0
2 | 2 | 6 | 7 | 7 | -1 | 0 | 1
(2 rows)
19) Path from \(12\) to \(10\)¶
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost FROM edges',
12, 10
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
(0 rows)
20) Path from \(12\) to \(7\)¶
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost FROM edges',
12, 7
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
(0 rows)
21) Using One to Many to get the solution of examples 17 and 18¶
Paths \(\{6\}\rightarrow\{10, 7\}\)
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost FROM edges',
6, ARRAY[10,7]
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 7 | 6 | 4 | 1 | 0
2 | 2 | 6 | 7 | 7 | -1 | 0 | 1
(2 rows)
22) Using Many to One to get the solution of examples 18 and 20¶
Paths \(\{6, 12\}\rightarrow\{7\}\)
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost FROM edges',
ARRAY[6,12], 7
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 7 | 6 | 4 | 1 | 0
2 | 2 | 6 | 7 | 7 | -1 | 0 | 1
(2 rows)
23) Using Many to Many to get the solution of examples 17 to 20¶
Paths \(\{6, 12\}\rightarrow\{10, 7\}\)
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost FROM edges',
ARRAY[6, 12], ARRAY[10,7]
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 7 | 6 | 4 | 1 | 0
2 | 2 | 6 | 7 | 7 | -1 | 0 | 1
(2 rows)
24) Using Combinations to get the solution of examples 17 to 19¶
Paths \(\{6\}\rightarrow\{10, 7\}\cup\{12\}\rightarrow\{10\}\)
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost FROM edges',
'SELECT * FROM (VALUES (6, 10), (6, 7), (12, 10)) AS combinations (source, target)'
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 7 | 6 | 4 | 1 | 0
2 | 2 | 6 | 7 | 7 | -1 | 0 | 1
(2 rows)
For undirected graphs only with cost column¶
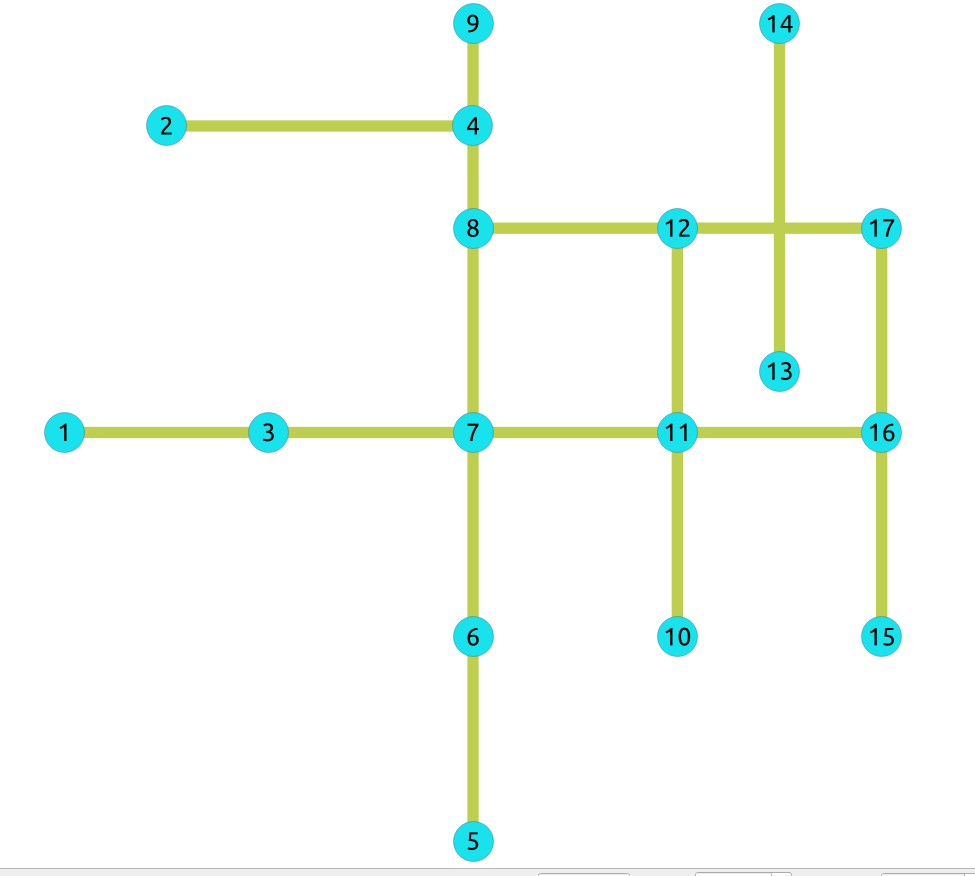
Undirected graph only with cost column¶
25) Path from \(6\) to \(10\)¶
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost FROM edges',
6, 10,
false
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 10 | 6 | 4 | 1 | 0
2 | 2 | 6 | 10 | 7 | 8 | 1 | 1
3 | 3 | 6 | 10 | 11 | 5 | 1 | 2
4 | 4 | 6 | 10 | 10 | -1 | 0 | 3
(4 rows)
26) Path from \(6\) to \(7\)¶
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost FROM edges',
6, 7,
false
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 7 | 6 | 4 | 1 | 0
2 | 2 | 6 | 7 | 7 | -1 | 0 | 1
(2 rows)
27) Path from \(12\) to \(10\)¶
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost FROM edges',
12, 10,
false
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 12 | 10 | 12 | 11 | 1 | 0
2 | 2 | 12 | 10 | 11 | 5 | 1 | 1
3 | 3 | 12 | 10 | 10 | -1 | 0 | 2
(3 rows)
28) Path from \(12\) to \(7\)¶
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost FROM edges',
12, 7,
false
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 12 | 7 | 12 | 12 | 1 | 0
2 | 2 | 12 | 7 | 8 | 10 | 1 | 1
3 | 3 | 12 | 7 | 7 | -1 | 0 | 2
(3 rows)
29) Using One to Many to get the solution of examples 25 and 26¶
Paths \(\{6\}\rightarrow\{10, 7\}\)
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost FROM edges',
6, ARRAY[10,7],
false
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 7 | 6 | 4 | 1 | 0
2 | 2 | 6 | 7 | 7 | -1 | 0 | 1
3 | 1 | 6 | 10 | 6 | 4 | 1 | 0
4 | 2 | 6 | 10 | 7 | 8 | 1 | 1
5 | 3 | 6 | 10 | 11 | 5 | 1 | 2
6 | 4 | 6 | 10 | 10 | -1 | 0 | 3
(6 rows)
30) Using Many to One to get the solution of examples 26 and 28¶
Paths \(\{6, 12\}\rightarrow\{7\}\)
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost FROM edges',
ARRAY[6,12], 7,
false
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 7 | 6 | 4 | 1 | 0
2 | 2 | 6 | 7 | 7 | -1 | 0 | 1
3 | 1 | 12 | 7 | 12 | 12 | 1 | 0
4 | 2 | 12 | 7 | 8 | 10 | 1 | 1
5 | 3 | 12 | 7 | 7 | -1 | 0 | 2
(5 rows)
31) Using Many to Many to get the solution of examples 25 to 28¶
Paths \(\{6, 12\}\rightarrow\{10, 7\}\)
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost FROM edges',
ARRAY[6, 12], ARRAY[10,7],
false
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 7 | 6 | 4 | 1 | 0
2 | 2 | 6 | 7 | 7 | -1 | 0 | 1
3 | 1 | 6 | 10 | 6 | 4 | 1 | 0
4 | 2 | 6 | 10 | 7 | 8 | 1 | 1
5 | 3 | 6 | 10 | 11 | 5 | 1 | 2
6 | 4 | 6 | 10 | 10 | -1 | 0 | 3
7 | 1 | 12 | 7 | 12 | 12 | 1 | 0
8 | 2 | 12 | 7 | 8 | 10 | 1 | 1
9 | 3 | 12 | 7 | 7 | -1 | 0 | 2
10 | 1 | 12 | 10 | 12 | 11 | 1 | 0
11 | 2 | 12 | 10 | 11 | 5 | 1 | 1
12 | 3 | 12 | 10 | 10 | -1 | 0 | 2
(12 rows)
32) Using Combinations to get the solution of examples 25 to 27¶
Paths \(\{6\}\rightarrow\{10, 7\}\cup\{12\}\rightarrow\{10\}\)
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost FROM edges',
'SELECT * FROM (VALUES (6, 10), (6, 7), (12, 10)) AS combinations (source, target)',
false
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 7 | 6 | 4 | 1 | 0
2 | 2 | 6 | 7 | 7 | -1 | 0 | 1
3 | 1 | 6 | 10 | 6 | 4 | 1 | 0
4 | 2 | 6 | 10 | 7 | 8 | 1 | 1
5 | 3 | 6 | 10 | 11 | 5 | 1 | 2
6 | 4 | 6 | 10 | 10 | -1 | 0 | 3
7 | 1 | 12 | 10 | 12 | 11 | 1 | 0
8 | 2 | 12 | 10 | 11 | 5 | 1 | 1
9 | 3 | 12 | 10 | 10 | -1 | 0 | 2
(9 rows)
Equvalences between signatures¶
The following examples find the path for \(\{6\}\rightarrow\{10\}\)
33) Using One to One¶
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost, reverse_cost FROM edges',
6, 10
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 10 | 6 | 4 | 1 | 0
2 | 2 | 6 | 10 | 7 | 8 | 1 | 1
3 | 3 | 6 | 10 | 11 | 9 | 1 | 2
4 | 4 | 6 | 10 | 16 | 16 | 1 | 3
5 | 5 | 6 | 10 | 15 | 3 | 1 | 4
6 | 6 | 6 | 10 | 10 | -1 | 0 | 5
(6 rows)
34) Using One to Many¶
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost, reverse_cost FROM edges',
6, ARRAY[10]
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 10 | 6 | 4 | 1 | 0
2 | 2 | 6 | 10 | 7 | 8 | 1 | 1
3 | 3 | 6 | 10 | 11 | 9 | 1 | 2
4 | 4 | 6 | 10 | 16 | 16 | 1 | 3
5 | 5 | 6 | 10 | 15 | 3 | 1 | 4
6 | 6 | 6 | 10 | 10 | -1 | 0 | 5
(6 rows)
35) Using Many to One¶
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost, reverse_cost FROM edges',
ARRAY[6], 10
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 10 | 6 | 4 | 1 | 0
2 | 2 | 6 | 10 | 7 | 8 | 1 | 1
3 | 3 | 6 | 10 | 11 | 9 | 1 | 2
4 | 4 | 6 | 10 | 16 | 16 | 1 | 3
5 | 5 | 6 | 10 | 15 | 3 | 1 | 4
6 | 6 | 6 | 10 | 10 | -1 | 0 | 5
(6 rows)
36) Using Many to Many¶
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost, reverse_cost FROM edges',
ARRAY[6], ARRAY[10]
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 10 | 6 | 4 | 1 | 0
2 | 2 | 6 | 10 | 7 | 8 | 1 | 1
3 | 3 | 6 | 10 | 11 | 9 | 1 | 2
4 | 4 | 6 | 10 | 16 | 16 | 1 | 3
5 | 5 | 6 | 10 | 15 | 3 | 1 | 4
6 | 6 | 6 | 10 | 10 | -1 | 0 | 5
(6 rows)
37) Using Combinations¶
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost, reverse_cost FROM edges',
'SELECT * FROM (VALUES(6, 10)) AS combinations (source, target)'
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 10 | 6 | 4 | 1 | 0
2 | 2 | 6 | 10 | 7 | 8 | 1 | 1
3 | 3 | 6 | 10 | 11 | 9 | 1 | 2
4 | 4 | 6 | 10 | 16 | 16 | 1 | 3
5 | 5 | 6 | 10 | 15 | 3 | 1 | 4
6 | 6 | 6 | 10 | 10 | -1 | 0 | 5
(6 rows)
See Also¶
The queries use the Sample Data network.
Indices and tables