pgr_bipartite -Experimental¶
pgr_bipartite — Disjoint sets of vertices such that no two vertices within
the same set are adjacent.

Boost Graph Inside¶
Warning
Possible server crash
These functions might create a server crash
Warning
Experimental functions
They are not officially of the current release.
They likely will not be officially be part of the next release:
The functions might not make use of ANY-INTEGER and ANY-NUMERICAL
Name might change.
Signature might change.
Functionality might change.
pgTap tests might be missing.
Might need c/c++ coding.
May lack documentation.
Documentation if any might need to be rewritten.
Documentation examples might need to be automatically generated.
Might need a lot of feedback from the comunity.
Might depend on a proposed function of pgRouting
Might depend on a deprecated function of pgRouting
Availability
Version 3.2.0
New experimental signature
Description¶
A bipartite graph is a graph with two sets of vertices which are connected to each other, but not within themselves. A bipartite graph is possible if the graph coloring is possible using two colors such that vertices in a set are colored with the same color.
The main Characteristics are:
The algorithm works in undirected graph only.
The returned values are not ordered.
The algorithm checks graph is bipartite or not. If it is bipartite then it returns the node along with two colors 0 and 1 which represents two different sets.
If graph is not bipartite then algorithm returns empty set.
Running time:
Signatures¶
(vertex_id, color_id)- Example:
When the graph is bipartite
SELECT * FROM pgr_bipartite(
$$SELECT id, source, target, cost, reverse_cost FROM edges$$
) ORDER BY vertex_id;
vertex_id | color_id
-----------+----------
1 | 0
2 | 0
3 | 1
4 | 1
5 | 0
6 | 1
7 | 0
8 | 1
9 | 0
10 | 0
11 | 1
12 | 0
13 | 0
14 | 1
15 | 1
16 | 0
17 | 1
(17 rows)
Parameters¶
Parameter |
Type |
Description |
|---|---|---|
|
Edges SQL as described below. |
Inner Queries¶
Edges SQL¶
Column |
Type |
Default |
Description |
|---|---|---|---|
|
ANY-INTEGER |
Identifier of the edge. |
|
|
ANY-INTEGER |
Identifier of the first end point vertex of the edge. |
|
|
ANY-INTEGER |
Identifier of the second end point vertex of the edge. |
|
|
ANY-NUMERICAL |
Weight of the edge ( |
|
|
ANY-NUMERICAL |
-1 |
Weight of the edge (
|
Where:
- ANY-INTEGER:
SMALLINT,INTEGER,BIGINT- ANY-NUMERICAL:
SMALLINT,INTEGER,BIGINT,REAL,FLOAT
Result Columns¶
Returns SET OF (vertex_id, color_id)
Column |
Type |
Description |
|---|---|---|
|
|
Identifier of the vertex. |
|
|
Identifier of the color of the vertex.
|
Additional Example¶
- Example:
The odd length cyclic graph can not be bipartite.
The edge
INSERT INTO edges (source, target, cost, reverse_cost) VALUES
(5, 1, 1, 1);
INSERT 0 1
Edges in blue represent odd length cycle subgraph.
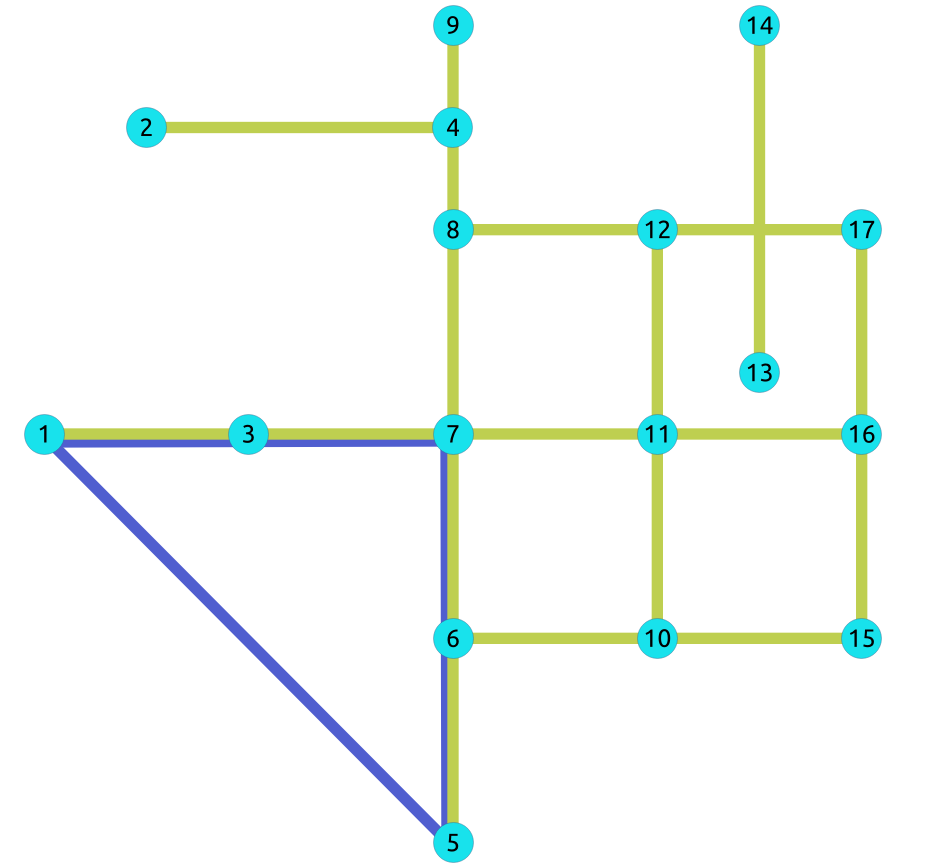
SELECT * FROM pgr_bipartite(
$$SELECT id, source, target, cost, reverse_cost FROM edges$$
);
vertex_id | color_id
-----------+----------
(0 rows)
See Also¶
Sample Data network.
Indices and tables
