pgr_bipartite -Experimental

pgr_bipartite — Disjoint sets of vertices such that no two vertices within the same set are adjacent.

Boost Graph Inside

Warning

Possible server crash

• These functions might create a server crash

Warning

Experimental functions

• They are not officially of the current release.

• They likely will not be officially be part of the next release:

  • The functions might not make use of ANY-INTEGER and ANY-NUMERICAL

  • Name might change.

  • Signature might change.

  • Functionality might change.

  • pgTap tests might be missing.

  • Might need c/c++ coding.

  • May lack documentation.

  • Documentation if any might need to be rewritten.

  • Documentation examples might need to be automatically generated.

  • Might need a lot of feedback from the comunity.

  • Might depend on a proposed function of pgRouting

  • Might depend on a deprecated function of pgRouting

Availability

• Version 3.2.0

  • New experimental signature

Description

A bipartite graph is a graph with two sets of vertices which are connected to each other, but not within themselves. A bipartite graph is possible if the graph coloring is possible using two colors such that vertices in a set are colored with the same color.

The main Characteristics are:

• The algorithm works in undirected graph only.

• The returned values are not ordered.

• The algorithm checks graph is bipartite or not. If it is bipartite then it returns the node along with two colors 0 and 1 which represents two different sets.

• If graph is not bipartite then algorithm returns empty set.

• Running time: \(O(V + E)\)

Signatures

pgr_bipartite(Edges SQL)

Returns set of (vertex_id, color_id)

OR EMPTY SET

Example:

When the graph is bipartite

SELECT * FROM pgr_bipartite(
    $$SELECT id, source, target, cost, reverse_cost FROM edges$$
) ORDER BY vertex_id;
 vertex_id | color_id
-----------+----------
         1 |        0
         2 |        0
         3 |        1
         4 |        1
         5 |        0
         6 |        1
         7 |        0
         8 |        1
         9 |        0
        10 |        0
        11 |        1
        12 |        0
        13 |        0
        14 |        1
        15 |        1
        16 |        0
        17 |        1
(17 rows)

Parameters

Parameter	Type	Description
Edges SQL	TEXT	Edges SQL as described below.

Inner Queries

Edges SQL

Column	Type	Default	Description
id	ANY-INTEGER		Identifier of the edge.
source	ANY-INTEGER		Identifier of the first end point vertex of the edge.
target	ANY-INTEGER		Identifier of the second end point vertex of the edge.
cost	ANY-NUMERICAL		Weight of the edge (source, target)
reverse_cost	ANY-NUMERICAL	-1	Weight of the edge (target, source) When negative: edge (target, source) does not exist, therefore it’s not part of the graph.

Where:

ANY-INTEGER:

SMALLINT, INTEGER, BIGINT

ANY-NUMERICAL:

SMALLINT, INTEGER, BIGINT, REAL, FLOAT

Result columns

Returns set of (vertex_id, color_id)

Column	Type	Description
vertex_id	BIGINT	Identifier of the vertex.
color_id	BIGINT	Identifier of the color of the vertex. The minimum value of color is 1.

Additional Example

Example:

The odd length cyclic graph can not be bipartite.

The edge \(5 \rightarrow 1\) will make subgraph with vertices \(\{1, 3, 7, 6, 5\}\) an odd length cyclic graph, as the cycle has 5 vertices.

INSERT INTO edges (source, target, cost, reverse_cost) VALUES
(5, 1, 1, 1);
INSERT 0 1

Edges in blue represent odd length cycle subgraph.

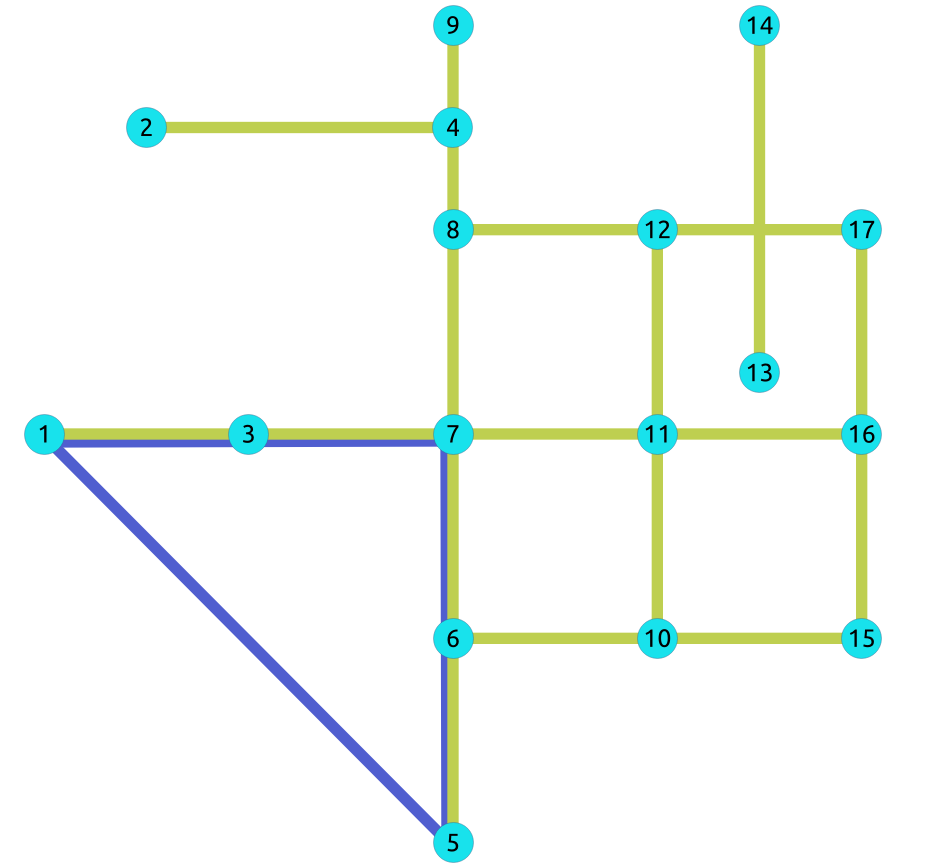
SELECT * FROM pgr_bipartite(
    $$SELECT id, source, target, cost, reverse_cost FROM edges$$
);
 vertex_id | color_id
-----------+----------
(0 rows)

See Also

• Boost: is_bipartite

• Wikipedia: bipartite graph

• Sample Data network.

Indices and tables

• Index

• Search Page