Contraction - Familia de funciones

• pgr_contraction

Introducción

En grafos grandes, como los grafos de carretera o de redes eléctricas, la contracción de grafos se puede utilizar para acelerar algunos algoritmos. La contracción reduce el tamaño del grafo eliminando algunos de los vértices y aristas, por ejemplo, podría agregar aristas que representen una secuencia de las aristas originales disminuyendo el tiempo total y el espacio utilizados en los algoritmos de grafos.

Esta implementación proporciona un marco flexible para agregar algoritmos de contracción en el futuro, actualmente, admite dos algoritmos:

1. Contracción sin salida

2. Contracción lineal

Permitiendo que el usuario:

• Prohíba la contracción en un conjunto de nodos.

• Decida el orden de los algoritmos de contracción y establezca el número máximo de veces que se van a ejecutar.

Contracción sin salida

Contracción de los nodos de hoja del grafo.

Sin salida

Un nodo se considera sin salida cuando

• En grafos no dirigidos:

  • El número de vértices adyacentes es 1.

• En grafos dirigidos:

  • El número de vértices adyacentes es 1.

  • No hay aristas salientes y tiene al menos una arista entrante.

  • No hay aristas entrantes y tiene al menos una arista saliente.

Cuando las condiciones son verdaderas, se puede hacer la Operación: Contracción de callejón sin salida.

Vértice sin salida en un grafo sin dirigir

• Los nodos verdes son nodos dead end

• Los nodos azules tienen un número ilimitado de aristas.

Nodo	Nodos adyacentes	Número de vértices adyacentes
\(a\)	\(\{u\}\)	1
\(b\)	\(\{v\}\)	1

Vértice sin salida en un grafo dirigido

• Los nodos verdes son nodos dead end

• Los nodos azules tienen un número ilimitado de aristas entrantes y/o salientes.

Nodo	Nodos adyacentes	Número de vértices adyacentes	Número de aristas entrantes	Número de aristas salientes
\(a\)	\(\{u\}\)	1
\(b\)	\(\{v\}\)	1
\(c\)	\(\{v, w\}\)	2	2	0
\(d\)	\(\{x\}\)	1
\(e\)	\(\{x, y\}\)	2	0	2

De arriba, nodes \(\{a, b, d\}\) son callejones sin salida por que el número de vértices adyacentes es 1. No son necesarios los checks para esos nodos.

En al siguiente tabla, nodos \(\{c, e\}\) por que el par del numero de vértices adyacentes no es 1 para

• \(c\)

  • No hay aristas salientes y tiene al menos una arista entrante.

• \(e\)

  • No hay aristas entrantes y tiene al menos una arista saliente.

Operación: Contracción sin salida

La contracción sin salida se detendrá hasta que no haya más nodos sin salida. Por ejemplo, del siguiente grafo donde \(w\) es el nodo dead end:

Después de contraer \(w\), el nodo ` \(v\) es ahora un nodo dead end y es contraído:

Después de contraer math:v, detenerse El nodo math:u tiene la información de los nodos que se contraen.

El nodo \(u\) tiene la información de los nodos que se contrajeron.

Contracción lineal

En el algoritmo, la contracción lineal es representada con un 2.

Lineal

En el caso de un grafo no dirigido, un nodo se considera un nodo lineal cuando

• El número de vértices adyacentes es 2.

En el caso de un grafo dirigido, un nodo se considera lineal cuando

• El número de vértices adyacentes es 2.

• La linealidad es simétrica

Vértice lineal en grafo no dirigido

• Los nodos verdes son lineales

• Los nodos azules tienen un número ilimitado de aristas entrantes y salientes.

No dirigido

Nodo	Nodos adyacentes	Número de vértices adyacentes
\(v\)	\(\{u, w\}\)	2

Vértice lineal en grafo dirigido

• Los nodos verdes son lineales

• Los nodos azules tienen un número ilimitado de aristas entrantes y salientes.

• El nodo blanco no es linero por que la linealidad no es simétrica.

  • Es posible ir a \(y \rightarrow c \rightarrow z\)

  • No es posible ir a \(z \rightarrow c \rightarrow y\)

Nodo	Nodos adyacentes	Número de vértices adyacentes	Es simétrico?
\(a\)	\(\{u, v\}\)	2	sí
\(b\)	\(\{w, x\}\)	2	sí
\(c\)	\(\{y, z\}\)	2	no

Operación: Contracción Lineal

La contracción lineal se detendrá hasta que no hayan más nodos lineales. Por ejemplo, en el siguiente grafo donde ` \(v\) y \(w\) son nodos lineales :

Contrayendo \(w\),

• El vértice \(w\) se elimina del grafo

• Los aristas \(v \rightarrow w\) y \(w \rightarrow z\) fueron eliminados del grafo.

• Se inserta un nuevo arista \(v \rightarrow z\) y se representa con color rojo.

Contrayendo \(v\):

• El vértice \(v\) se elimina del grafo

• Los aristas \(u \rightarrow v\) y \(v \rightarrow z\) son removidos del grafo.

• Se inserta un nuevo arista \(u \rightarrow z\) y se representa con color rojo.

El arista \(u \rightarrow z\) tiene la información de los nodos que fueron contraídos.

El ciclo

Contraer un grafo se puede hacer con más de una operación. El orden de las operaciones afecta al gráfico contraído resultante; después de aplicar una operación, el conjunto de vértices que se pueden contraer con otra operación cambia.

Esta implementación alterna los tiempos `` max_cycles`` a través de `` operations_order``.

<input>
do max_cycles times {
    for (operation in operations_order)
     { do operation }
}
<output>

Contracción de los datos de muestra

En esta sección, la creación y el uso de un grafo contraído se mostrarán en el ejemplo.

• Se usa Datos Muestra para un grafo no dirigido

• una operación sin salida primero seguida de una operación lineal.

Construcción del grafo en la base de datos

Datos Originales

La siguiente consulta muestra los datos originales implicados en la operación de contracción.

SELECT id, source, target, cost, reverse_cost
FROM edges ORDER BY id;
 id | source | target | cost | reverse_cost
----+--------+--------+------+--------------
  1 |      5 |      6 |    1 |            1
  2 |      6 |     10 |   -1 |            1
  3 |     10 |     15 |   -1 |            1
  4 |      6 |      7 |    1 |            1
  5 |     10 |     11 |    1 |           -1
  6 |      1 |      3 |    1 |            1
  7 |      3 |      7 |    1 |            1
  8 |      7 |     11 |    1 |            1
  9 |     11 |     16 |    1 |            1
 10 |      7 |      8 |    1 |            1
 11 |     11 |     12 |    1 |           -1
 12 |      8 |     12 |    1 |           -1
 13 |     12 |     17 |    1 |           -1
 14 |      8 |      9 |    1 |            1
 15 |     16 |     17 |    1 |            1
 16 |     15 |     16 |    1 |            1
 17 |      2 |      4 |    1 |            1
 18 |     13 |     14 |    1 |            1
(18 rows)

El grafo original:

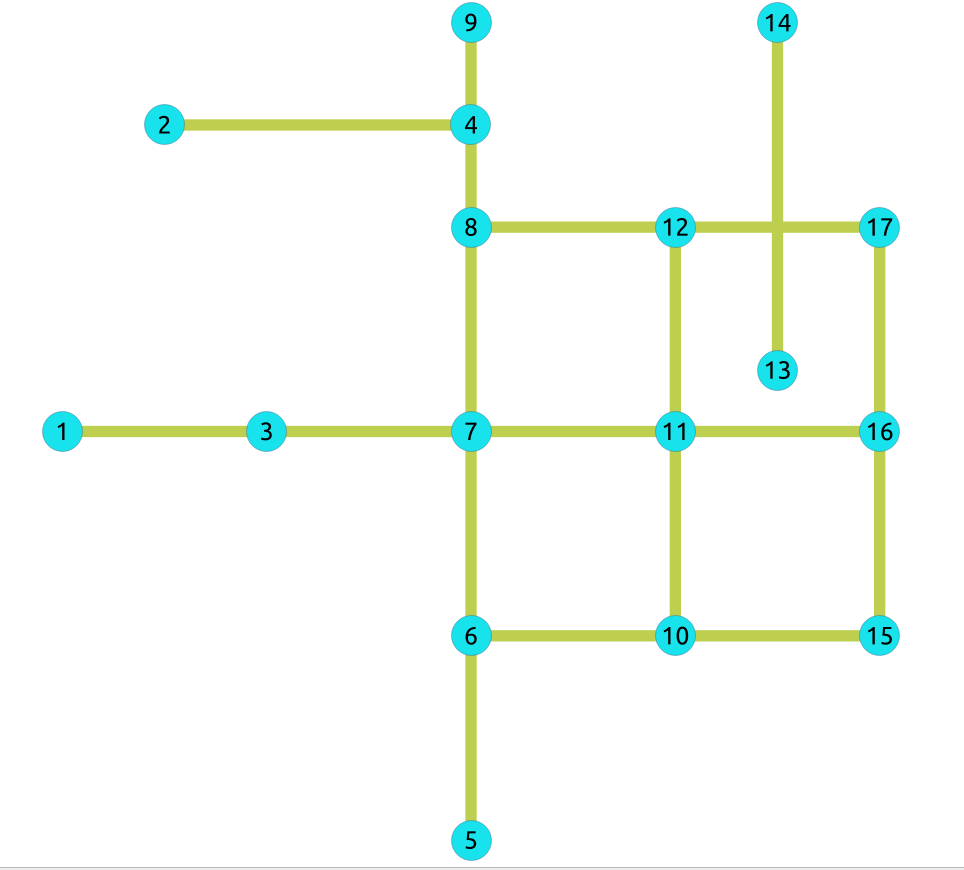
Resultados de la Contracción

Los resultados no representan al grafo contraído. Representan los cambios realizados en el grafo después de aplicar el algoritmo de contracción.

Observe que los vértices, por ejemplo, \(6\) , no aparecen en los resultados porque no se vieron afectados por el algoritmo de contracción.

SELECT * FROM pgr_contraction(
  'SELECT id, source, target, cost, reverse_cost FROM edges',
  array[1, 2], directed => false);
 type | id | contracted_vertices | source | target | cost
------+----+---------------------+--------+--------+------
 v    |  4 | {2}                 |     -1 |     -1 |   -1
 v    |  7 | {1,3}               |     -1 |     -1 |   -1
 v    | 14 | {13}                |     -1 |     -1 |   -1
 e    | -1 | {5,6}               |      7 |     10 |    2
 e    | -2 | {8,9}               |      7 |     12 |    2
 e    | -3 | {17}                |     12 |     16 |    2
 e    | -4 | {15}                |     10 |     16 |    2
(7 rows)

Después de realizar la operación de contracción sin salida:

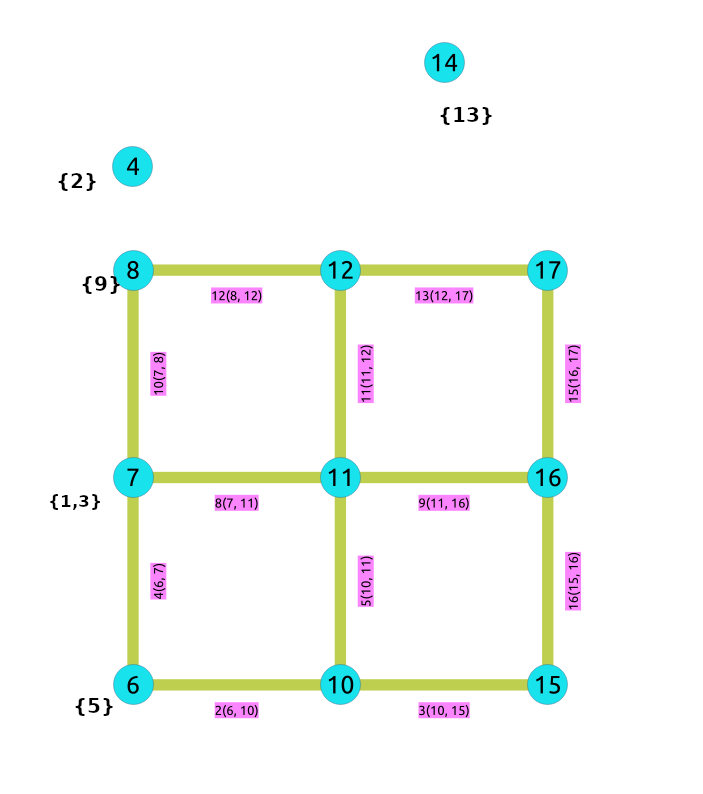
Después de hacer la operación de contracción lineal al grafo anterior:

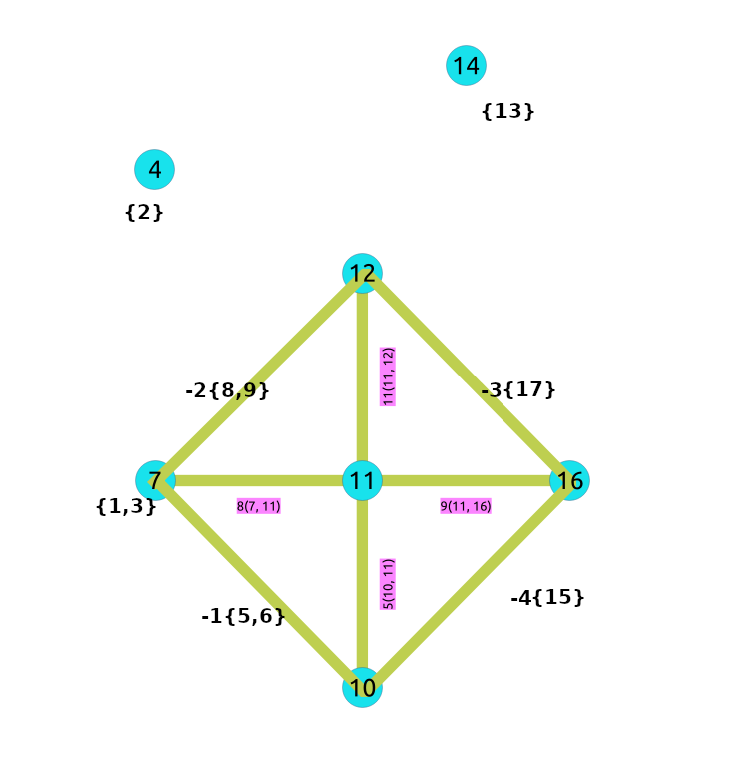
El proceso para crear el grafo de contracción en la base de datos:

Añadir columnas adicionales

Agregar de columnas adicionales a las tablas edge_table y edge_table_vertices_pgr donde:

Columna	Descripción
contracted_vertices	El conjunto de vértices que pertenecen al vértice/arista
is_contracted	En la tabla de vértices En caso de “”true”” se contrae el vértice, no forma parte del grafo contraído. En caso de “”false”” el vértice no se contrae, su parte del grafo contraído.
is_new	En la tabla de aristas En caso de `` true``, la arista se generó por el algoritmo de contracción. Es parte del grafo contraído. En caso de false , la arista es una arista original, podría ser o no parte del grafo contraído.

ALTER TABLE vertices ADD is_contracted BOOLEAN DEFAULT false;
ALTER TABLE
ALTER TABLE vertices ADD contracted_vertices BIGINT[];
ALTER TABLE
ALTER TABLE edges ADD is_new BOOLEAN DEFAULT false;
ALTER TABLE
ALTER TABLE edges ADD contracted_vertices BIGINT[];
ALTER TABLE

Almacenar información de contracción

Almacenar los resultados de la contracción en una tabla

SELECT * INTO contraction_results
FROM pgr_contraction(
  'SELECT id, source, target, cost, reverse_cost FROM edges',
  array[1, 2], directed => false);
SELECT 7

Actualización de la tabla de vértices

Usar la columna is_contracted para indicar los vértices contraídos.

UPDATE vertices
SET is_contracted = true
WHERE id IN (SELECT  unnest(contracted_vertices) FROM  contraction_results);
UPDATE 10

Lllena contracted_vertices con la información de los resultados que pertenecen a los vértices.

UPDATE vertices
SET contracted_vertices = contraction_results.contracted_vertices
FROM contraction_results
WHERE type = 'v' AND vertices.id = contraction_results.id;
UPDATE 3

La tabla de vértices modificada:

SELECT id, contracted_vertices, is_contracted
FROM vertices
ORDER BY id;
 id | contracted_vertices | is_contracted
----+---------------------+---------------
  1 |                     | t
  2 |                     | t
  3 |                     | t
  4 | {2}                 | f
  5 |                     | t
  6 |                     | t
  7 | {1,3}               | f
  8 |                     | t
  9 |                     | t
 10 |                     | f
 11 |                     | f
 12 |                     | f
 13 |                     | t
 14 | {13}                | f
 15 |                     | t
 16 |                     | f
 17 |                     | t
(17 rows)

Actialización de la tabla de aristas

Inserte las nuevas aristas generadas por pgr_contraction.

INSERT INTO edges(source, target, cost, reverse_cost, contracted_vertices, is_new)
SELECT source, target, cost, -1, contracted_vertices, true
FROM contraction_results
WHERE type = 'e';
INSERT 0 4

La modificada edge_table.

SELECT id, source, target, cost, reverse_cost, contracted_vertices, is_new
FROM edges
ORDER BY id;
 id | source | target | cost | reverse_cost | contracted_vertices | is_new
----+--------+--------+------+--------------+---------------------+--------
  1 |      5 |      6 |    1 |            1 |                     | f
  2 |      6 |     10 |   -1 |            1 |                     | f
  3 |     10 |     15 |   -1 |            1 |                     | f
  4 |      6 |      7 |    1 |            1 |                     | f
  5 |     10 |     11 |    1 |           -1 |                     | f
  6 |      1 |      3 |    1 |            1 |                     | f
  7 |      3 |      7 |    1 |            1 |                     | f
  8 |      7 |     11 |    1 |            1 |                     | f
  9 |     11 |     16 |    1 |            1 |                     | f
 10 |      7 |      8 |    1 |            1 |                     | f
 11 |     11 |     12 |    1 |           -1 |                     | f
 12 |      8 |     12 |    1 |           -1 |                     | f
 13 |     12 |     17 |    1 |           -1 |                     | f
 14 |      8 |      9 |    1 |            1 |                     | f
 15 |     16 |     17 |    1 |            1 |                     | f
 16 |     15 |     16 |    1 |            1 |                     | f
 17 |      2 |      4 |    1 |            1 |                     | f
 18 |     13 |     14 |    1 |            1 |                     | f
 19 |      7 |     10 |    2 |           -1 | {5,6}               | t
 20 |      7 |     12 |    2 |           -1 | {8,9}               | t
 21 |     12 |     16 |    2 |           -1 | {17}                | t
 22 |     10 |     16 |    2 |           -1 | {15}                | t
(22 rows)

El grafo contraído

Vértices que pertenecen al grafo contraído.

SELECT id
FROM vertices
WHERE is_contracted = false
ORDER BY id;
 id
----
  4
  7
 10
 11
 12
 14
 16
(7 rows)

Aristas que pertenecen al grafo contraído.

WITH
vertices_in_graph AS (
  SELECT id
  FROM vertices
  WHERE is_contracted = false
)
SELECT id, source, target, cost, reverse_cost, contracted_vertices
FROM edges
WHERE source IN (SELECT * FROM vertices_in_graph)
AND target IN (SELECT * FROM vertices_in_graph)
ORDER BY id;
 id | source | target | cost | reverse_cost | contracted_vertices
----+--------+--------+------+--------------+---------------------
  5 |     10 |     11 |    1 |           -1 |
  8 |      7 |     11 |    1 |            1 |
  9 |     11 |     16 |    1 |            1 |
 11 |     11 |     12 |    1 |           -1 |
 19 |      7 |     10 |    2 |           -1 | {5,6}
 20 |      7 |     12 |    2 |           -1 | {8,9}
 21 |     12 |     16 |    2 |           -1 | {17}
 22 |     10 |     16 |    2 |           -1 | {15}
(8 rows)

El grafo contraído

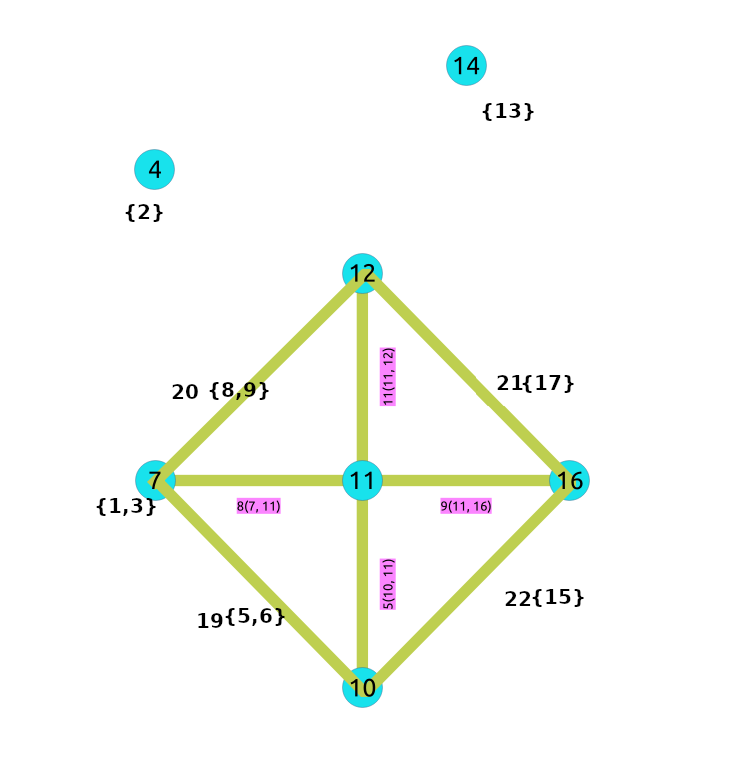
Usando el grafo contraído

Uso del grafo contraído con pgr_dijkstra

Hay tres casos al calcular la ruta más corta entre un origen y un destino determinados en un grafo contraído:

• Caso 1: Tanto el origen como el destino pertenecen al grafo contraído.

• Caso 2: El origen y/o el destino pertenecen a un subgrafo de aristas.

• Caso 3: El origen y/o el destino pertenecen a un vértice.

Caso 1: Tanto el origen como el destino pertenecen al grafo contraído.

Usando las Aristas que pertenecen al grafo contraído. en las líneas 10 a 19.

CREATE OR REPLACE FUNCTION my_dijkstra(
  departure BIGINT, destination BIGINT,
  OUT seq INTEGER, OUT path_seq INTEGER,
  OUT node BIGINT, OUT edge BIGINT,
  OUT cost FLOAT, OUT agg_cost FLOAT)
RETURNS SETOF RECORD AS
$BODY$
SELECT * FROM pgr_dijkstra(
  $$
  WITH
  vertices_in_graph AS (
    SELECT id
    FROM vertices
    WHERE is_contracted = false
  )
  SELECT id, source, target, cost, reverse_cost
  FROM edges
  WHERE source IN (SELECT * FROM vertices_in_graph)
  AND target IN (SELECT * FROM vertices_in_graph)
  $$,
  departure, destination, false);
$BODY$
LANGUAGE SQL VOLATILE;
CREATE FUNCTION

Caso 1

Cuando el origen y el destino pertenecen al grafo contraído, se encuentra ruta.

SELECT * FROM my_dijkstra(10, 12);
 seq | path_seq | node | edge | cost | agg_cost
-----+----------+------+------+------+----------
   1 |        1 |   10 |    5 |    1 |        0
   2 |        2 |   11 |   11 |    1 |        1
   3 |        3 |   12 |   -1 |    0 |        2
(3 rows)

Caso 2

Cuando el origen y/o el destino pertenecen a un subgrafo de aristas, no se encuentra una ruta.

En este caso, el grafo contraído no tiene una arista que se conecte con el nodo \(4\).

SELECT * FROM my_dijkstra(15, 12);
 seq | path_seq | node | edge | cost | agg_cost
-----+----------+------+------+------+----------
(0 rows)

Caso 3

Cuando el origen y/o el destino pertenecen a un vértice, no se encuentra ruta.

En este caso, el grafo contraído no tiene algún arista que conecte con el nodo \(7\) ni con el nodo \(4\) del segundo caso.

SELECT * FROM my_dijkstra(15, 1);
 seq | path_seq | node | edge | cost | agg_cost
-----+----------+------+------+------+----------
(0 rows)

Caso 2: El origen y/o el destino pertenecen a un subgrafo de aristas.

Refinar la función anterior para incluir nodos que pertenezcan a una arista.

• Los vértices que deben ampliarse se calculan en las líneas 10 a 16.

• Añadiendo al grafo contraído esa sección adicional en las líneas 25 a 27.

CREATE OR REPLACE FUNCTION my_dijkstra(
  departure BIGINT, destination BIGINT,
  OUT seq INTEGER, OUT path_seq INTEGER,
  OUT node BIGINT, OUT edge BIGINT,
  OUT cost FLOAT, OUT agg_cost FLOAT)
RETURNS SETOF RECORD AS
$BODY$
SELECT * FROM pgr_dijkstra(
  $$
  WITH
  edges_to_expand AS (
    SELECT id
    FROM edges
    WHERE ARRAY[$$ || departure || $$]::BIGINT[] <@ contracted_vertices
    OR ARRAY[$$ || destination || $$]::BIGINT[] <@ contracted_vertices
  ),

  vertices_in_graph AS (
    SELECT id
    FROM vertices
    WHERE is_contracted = false

    UNION

    SELECT unnest(contracted_vertices)
    FROM edges
    WHERE id IN (SELECT id FROM edges_to_expand)
  )

  SELECT id, source, target, cost, reverse_cost
  FROM edges
  WHERE source IN (SELECT * FROM vertices_in_graph)
  AND target IN (SELECT * FROM vertices_in_graph)
  $$,
  departure, destination, false);
$BODY$
LANGUAGE SQL VOLATILE;
CREATE FUNCTION

Caso 1

Cuando el origen y el destino pertenecen al grafo contraído, se encuentra ruta.

SELECT * FROM my_dijkstra(10, 12);
 seq | path_seq | node | edge | cost | agg_cost
-----+----------+------+------+------+----------
   1 |        1 |   10 |    5 |    1 |        0
   2 |        2 |   11 |   11 |    1 |        1
   3 |        3 |   12 |   -1 |    0 |        2
(3 rows)

Caso 2

Cuando el origen y/o el destino pertenecen a un subgrafo de arista, entonces se encuentra una ruta.

El grafo de ruteo ahora tiene un arista que se conecta con el nodo \(4\).

SELECT * FROM my_dijkstra(15, 12);
 seq | path_seq | node | edge | cost | agg_cost
-----+----------+------+------+------+----------
   1 |        1 |   15 |   16 |    1 |        0
   2 |        2 |   16 |   21 |    2 |        1
   3 |        3 |   12 |   -1 |    0 |        3
(3 rows)

Caso 3

Cuando el origen y/o el destino pertenecen a un vértice, no se encuentra ruta.

En este caso, el grafo contraído no tiene una arista que se conecte con el nodo \(7\).

SELECT * FROM my_dijkstra(15, 1);
 seq | path_seq | node | edge | cost | agg_cost
-----+----------+------+------+------+----------
(0 rows)

Caso 3: El origen y/o el destino pertenecen a un vértice.

Refinar la función anterior para incluir nodos que pertenezcan a una arista.

• Los vértices que deben ampliarse se calculan en las líneas 18 a 23.

• Añadiendo al grafo contraído esa sección adicional en las líneas 38 a 40.

CREATE OR REPLACE FUNCTION my_dijkstra(
  departure BIGINT, destination BIGINT,
  OUT seq INTEGER, OUT path_seq INTEGER,
  OUT node BIGINT, OUT edge BIGINT,
  OUT cost FLOAT, OUT agg_cost FLOAT)
RETURNS SETOF RECORD AS
$BODY$
SELECT * FROM pgr_dijkstra(
  $$
  WITH
  edges_to_expand AS (
    SELECT id
    FROM edges
    WHERE ARRAY[$$ || departure || $$]::BIGINT[] <@ contracted_vertices
    OR ARRAY[$$ || destination || $$]::BIGINT[] <@ contracted_vertices
  ),

  vertices_to_expand AS (
    SELECT id
    FROM vertices
    WHERE ARRAY[$$ || departure || $$]::BIGINT[] <@ contracted_vertices
    OR ARRAY[$$ || destination || $$]::BIGINT[] <@ contracted_vertices
  ),

  vertices_in_graph AS (
    SELECT id
    FROM vertices
    WHERE is_contracted = false

    UNION

    SELECT unnest(contracted_vertices)
    FROM edges
    WHERE id IN (SELECT id FROM edges_to_expand)

    UNION

    SELECT unnest(contracted_vertices)
    FROM vertices
    WHERE id IN (SELECT id FROM vertices_to_expand)
  )

  SELECT id, source, target, cost, reverse_cost
  FROM edges
  WHERE source IN (SELECT * FROM vertices_in_graph)
  AND target IN (SELECT * FROM vertices_in_graph)
  $$,
  departure, destination, false);
$BODY$
LANGUAGE SQL VOLATILE;
CREATE FUNCTION

Caso 1

Cuando el origen y el destino pertenecen al grafo contraído, se encuentra ruta.

SELECT * FROM my_dijkstra(10, 12);
 seq | path_seq | node | edge | cost | agg_cost
-----+----------+------+------+------+----------
   1 |        1 |   10 |    5 |    1 |        0
   2 |        2 |   11 |   11 |    1 |        1
   3 |        3 |   12 |   -1 |    0 |        2
(3 rows)

Caso 2

El cambio de código no afecta a este caso, por lo que cuando el origen o el destino pertenecen a un subgrafo de aristas, aún se puede encontrar ruta.

SELECT * FROM my_dijkstra(15, 12);
 seq | path_seq | node | edge | cost | agg_cost
-----+----------+------+------+------+----------
   1 |        1 |   15 |   16 |    1 |        0
   2 |        2 |   16 |   21 |    2 |        1
   3 |        3 |   12 |   -1 |    0 |        3
(3 rows)

Caso 3

Cuando el origen y/o el destino pertenecen a un vértice, entonces se encuentra ruta.

Ahora, el grafo de ruteo tiene un arista que se conecta con el nodo \(7\).

SELECT * FROM my_dijkstra(15, 1);
 seq | path_seq | node | edge | cost | agg_cost
-----+----------+------+------+------+----------
   1 |        1 |   15 |    3 |    1 |        0
   2 |        2 |   10 |   19 |    2 |        1
   3 |        3 |    7 |    7 |    1 |        3
   4 |        4 |    3 |    6 |    1 |        4
   5 |        5 |    1 |   -1 |    0 |        5
(5 rows)

Ver también

• pgr_contraction

• Datos Muestra

• https://www.cs.cmu.edu/afs/cs/academic/class/15210-f12/www/lectures/lecture16.pdf

• https://algo2.iti.kit.edu/documents/routeplanning/geisberger_dipl.pdf

Índices y tablas

• Índice

• Página de Búsqueda