Supported versions:

`pgr_lineGraphFull` - Experimental¶

pgr_lineGraphFull — Transforma un grafo dado en uno nuevo donde todos los vértices del grafo original se convierten en grafos de líneas.

Advertencia

Posible bloqueo del servidor

Estas funciones pueden crear una caída del servidor

Advertencia

Funciones experimentales

No son oficialmente de la versión actual.
Es probable que oficialmente no formen parte de la siguiente versión:
- Las funciones no podrían hacer uso de ANY-INTEGER ni ANY-NUMERICAL
- El nombre puede cambiar.
- La firma puede cambiar.
- La funcionalidad puede cambiar.
- Las pruebas de pgTap pueden faltar.
- Posiblemente necesite codificación c/c++.
- Puede carecer documentación.
- Hay documentación que, en dado caso, podría ser necesario reescribir.
- Puede ser necesario que los ejemplos de documentación se generen automáticamente.
- Puede ser necesaria retroalimentación por parte de la comunidad.
- Puede depender de una función propuesta de pgRouting
- Podría depender de una función obsoleta de pgRouting

Disponibilidad

Versión 2.6.0
- Nueva función Experimental

Descripción¶

pgr_lineGraphFull, convierte un grafo dirigido a un grafo dirigido lineal, convirtiendo cada vértice en un grafo completo y manteniendo todas las aristas originales. Las nuevas aristas de conexión tienen un costo de 0 y van entre las aristas originales adyacentes, respetando la direccionalidad.

Una posible aplicación del grafo resultante es «ruteo con restricciones en dos aristas»:

Establecer un coste de uso del vértice al enrutar entre aristas en la arista de conexión
Prohibir el ruteo entre dos aristas al quitar el arista de conexión

Esto es posible porque cada una de las intersecciones (vértices) en el grafo original ahora son grafos completos que tienen una nueva arista para cada posible giro a través de esa intersección.

Las principales características son:

Esta función es para grafos dirigidos.
Los resultados son indefinidos cuando se utiliza un identificador de vértice negativo en el grafo de entrada.
Los resultados son indefinidos cuando se utiliza un identificador de borde duplicado en el grafo de entrada.
Tiempo de ejecución: TBD

Firmas¶

Resumen

pgr_lineGraphFull(SQL de aristas)

RETURNS SET OF (seq, source, target, cost, edge)

OR EMPTY SET

Ejemplo:: Grafo de línea completa del subgrafo de las aristas \(\{4, 7, 8, 10\}\)

SELECT * FROM pgr_lineGraphFull(
  $$SELECT id, source, target, cost, reverse_cost
  FROM edges
  WHERE id IN (4, 7, 8, 10)$$);
 seq | source | target | cost | edge
-----+--------+--------+------+------
|     -1 |      7 |    1 |    4
|      6 |     -1 |    0 |    0
|     -2 |      6 |    1 |   -4
|     -3 |      3 |    1 |   -7
|     -4 |     11 |    1 |    8
|     -5 |      8 |    1 |   10
|      7 |     -2 |    0 |    0
|      7 |     -3 |    0 |    0
|      7 |     -4 |    0 |    0
|      7 |     -5 |    0 |    0
|     -6 |     -2 |    0 |    0
|     -6 |     -3 |    0 |    0
|     -6 |     -4 |    0 |    0
|     -6 |     -5 |    0 |    0
|     -7 |     -2 |    0 |    0
|     -7 |     -3 |    0 |    0
|     -7 |     -4 |    0 |    0
|     -7 |     -5 |    0 |    0
|     -8 |     -2 |    0 |    0
|     -8 |     -3 |    0 |    0
|     -8 |     -4 |    0 |    0
|     -8 |     -5 |    0 |    0
|     -9 |     -6 |    1 |    7
|      3 |     -9 |    0 |    0
|    -10 |     -7 |    1 |   -8
|     11 |    -10 |    0 |    0
|    -11 |     -8 |    1 |  -10
|      8 |    -11 |    0 |    0
(28 rows)

Parámetros¶

Parámetro	Tipo	Descripción
SQL de aristas	`TEXT`	SQL de aristas descritas más adelante.

Consultas Internas¶

SQL aristas¶

Columna	Tipo	x Defecto	Descripción
`id`	ENTEROS		Identificador de la arista.
`source`	ENTEROS		Identificador del primer vértice de la arista.
`target`	ENTEROS		Identificador del segundo vértice de la arista.
`cost`	FLOTANTES		Peso de la arista (`source`, `target`)
`reverse_cost`	FLOTANTES	-1	Peso de la arista (`target`, `source`) Cuando negativo: la arista (`target`, `source`) no existe, por lo tanto no es parte del grafo.

Donde:

ENTEROS:: SMALLINT, INTEGER, BIGINT
FLOTANTES:: SMALLINT, INTEGER, BIGINT, REAL, FLOAT

Columnas de Resultados¶

RETURNS SET OF (seq, source, target, cost, edge)

Columna	Tipo	Descripción
`seq`	`INTEGER`	Valor secuencial a partir de 1. Da un identificador local de la arista
`source`	`BIGINT`	Identificador del vértice de origen de la arista actual. Cuando es “negativo”: el origen es la arista inversa en el grafo original.
`target`	`BIGINT`	Identificador del vértice destino de la arista actual. Cuando es negativo: el destino es la arista inversa en el grafo original.
`cost`	`FLOAT`	Peso de la arista (`source`, `target`). Cuando negative: la arista (`source`, `target`) no existe, por lo tanto no es parte del grafo.
`reverse_cost`	`FLOAT`	Peso de la arista (`target`, `source`). Cuando negative: la arista (`target`, `source`) no existe, por lo tanto no es parte del grafo.

Ejemplos Adicionales¶

Los ejemplos de esta sección se basan en la red Datos Muestra. Los ejemplos incluyen el subgrafo que incluye las aristas 4, 7, 8 y 10 con reverse_cost.

The data ¶

En este ejemplo se muestra cómo funciona esta transformación de grafo para crear aristas adicionales para cada giro posible en un grafoáfico.

SELECT id, source, target, cost, reverse_cost
FROM edges
WHERE id IN (4, 7, 8, 10);
 id | source | target | cost | reverse_cost
----+--------+--------+------+--------------
  4 |      6 |      7 |    1 |            1
  7 |      3 |      7 |    1 |            1
  8 |      7 |     11 |    1 |            1
 10 |      7 |      8 |    1 |            1
(4 rows)

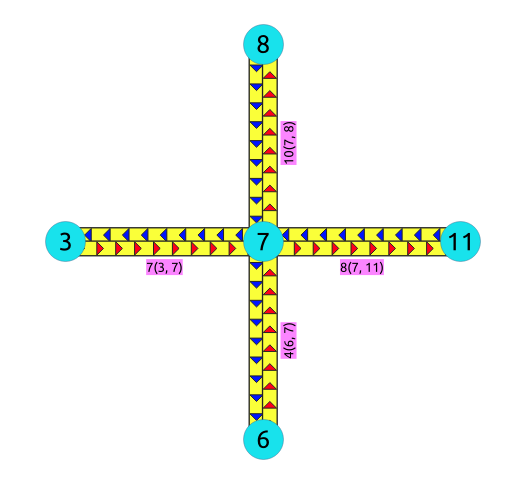
The transformation ¶

SELECT * FROM pgr_lineGraphFull(
  $$SELECT id, source, target, cost, reverse_cost
  FROM edges
  WHERE id IN (4, 7, 8, 10)$$);
 seq | source | target | cost | edge
-----+--------+--------+------+------
|     -1 |      7 |    1 |    4
|      6 |     -1 |    0 |    0
|     -2 |      6 |    1 |   -4
|     -3 |      3 |    1 |   -7
|     -4 |     11 |    1 |    8
|     -5 |      8 |    1 |   10
|      7 |     -2 |    0 |    0
|      7 |     -3 |    0 |    0
|      7 |     -4 |    0 |    0
|      7 |     -5 |    0 |    0
|     -6 |     -2 |    0 |    0
|     -6 |     -3 |    0 |    0
|     -6 |     -4 |    0 |    0
|     -6 |     -5 |    0 |    0
|     -7 |     -2 |    0 |    0
|     -7 |     -3 |    0 |    0
|     -7 |     -4 |    0 |    0
|     -7 |     -5 |    0 |    0
|     -8 |     -2 |    0 |    0
|     -8 |     -3 |    0 |    0
|     -8 |     -4 |    0 |    0
|     -8 |     -5 |    0 |    0
|     -9 |     -6 |    1 |    7
|      3 |     -9 |    0 |    0
|    -10 |     -7 |    1 |   -8
|     11 |    -10 |    0 |    0
|    -11 |     -8 |    1 |  -10
|      8 |    -11 |    0 |    0
(28 rows)

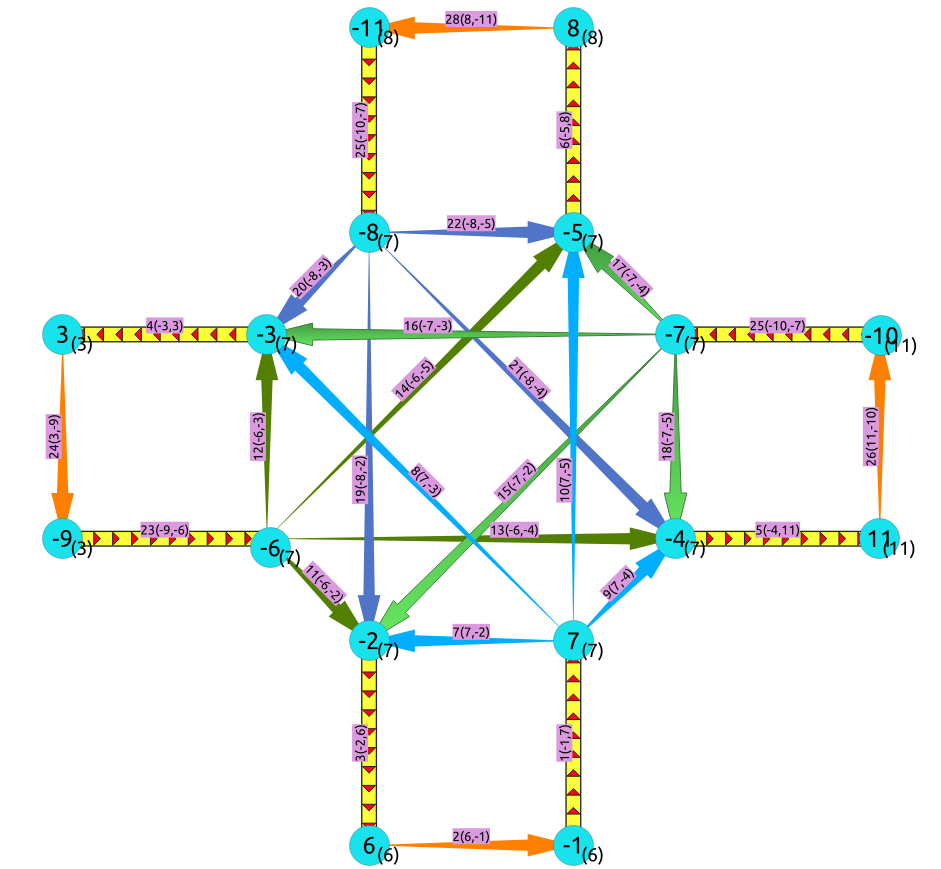
En el grafo transformado, todas las aristas del grafo original siguen presentes (amarillos), pero ahora hay aristas adicionales para cada giro que se podría hacer a través del vértice 7 (naranja).

Crear una tabla que identifica los vértices transformados ¶

Los vértices del grafo transformado se crean dividiendo los vértices en el grafo original. A menos que un vértice en el grafo original sea un vértice hoja, generará más de un vértice en el grafo transformado. A uno de los vértices recién creados en el grafo transformado se le dará el mismo identificador del vértice desde el cual se creó en el grafo original, pero el resto de los vértices recién creados tendrán identificadores de vértices negativos.

Following is an example of how to generate a table that maps the ids of the newly created vertices with the original vertex that they were created from

Store edge results ¶

The first step is to store the results of the pgr_lineGraphFull call into a table

SELECT seq AS id, source, target, cost, edge
INTO lineGraph_edges
FROM pgr_lineGraphFull(
  $$SELECT id, source, target, cost, reverse_cost
  FROM edges
  WHERE id IN (4, 7, 8, 10)$$);
SELECT 28

Create the mapping table ¶

From the original graph’s vertex information

SELECT id, NULL::BIGINT original_id
INTO vertex_map
FROM vertices;
SELECT 17

Add the new vertices

INSERT INTO vertex_map (id)
(SELECT id
FROM pgr_extractVertices(
  $$SELECT id, source, target FROM lineGraph_edges$$) WHERE id < 0);
INSERT 0 11

Filling the mapping table ¶

The positive vertex identifiers are the original identifiers

UPDATE vertex_map
SET original_id = id
WHERE id > 0;
UPDATE 17

Inspecting the vertices map

SELECT *
FROM vertex_map ORDER BY id DESC;
 id  | original_id
-----+-------------
  17 |          17
  16 |          16
  15 |          15
  14 |          14
  13 |          13
  12 |          12
  11 |          11
  10 |          10
   9 |           9
   8 |           8
   7 |           7
   6 |           6
   5 |           5
   4 |           4
   3 |           3
   2 |           2
   1 |           1
  -1 |
  -2 |
  -3 |
  -4 |
  -5 |
  -6 |
  -7 |
  -8 |
  -9 |
 -10 |
 -11 |
(28 rows)

The self loops happen when there is no cost traveling to the target and the source has an original value.

SELECT *, source AS targets_original_id
  FROM lineGraph_edges
  WHERE cost = 0 and source > 0;
 id | source | target | cost | edge | targets_original_id
----+--------+--------+------+------+---------------------
  2 |      6 |     -1 |    0 |    0 |                   6
  7 |      7 |     -2 |    0 |    0 |                   7
  8 |      7 |     -3 |    0 |    0 |                   7
  9 |      7 |     -4 |    0 |    0 |                   7
 10 |      7 |     -5 |    0 |    0 |                   7
 24 |      3 |     -9 |    0 |    0 |                   3
 26 |     11 |    -10 |    0 |    0 |                  11
 28 |      8 |    -11 |    0 |    0 |                   8
(8 rows)

Updating values from self loops

WITH
self_loops AS (
  SELECT DISTINCT source, target, source AS targets_original_id
  FROM lineGraph_edges
  WHERE cost = 0 and source > 0)
UPDATE vertex_map SET original_id = targets_original_id
FROM self_loops WHERE target = id;
UPDATE 8

Inspecting the vertices table

SELECT *
FROM vertex_map WHERE id < 0
ORDER BY id DESC;
 id  | original_id
-----+-------------
  -1 |           6
  -2 |           7
  -3 |           7
  -4 |           7
  -5 |           7
  -6 |
  -7 |
  -8 |
  -9 |           3
 -10 |          11
 -11 |           8
(11 rows)

Updating from inner self loops

WITH
assigned_vertices
AS (SELECT id, original_id
  FROM vertex_map
  WHERE original_id IS NOT NULL),
cross_edges
AS (SELECT DISTINCT e.source, v.original_id AS source_original_id
  FROM lineGraph_edges AS e
  JOIN vertex_map AS v ON (e.target = v.id)
  WHERE source NOT IN (SELECT id FROM assigned_vertices)
)
UPDATE vertex_map SET original_id = source_original_id
FROM cross_edges WHERE source = id;
UPDATE 3

Inspecting the vertices map

SELECT *
FROM vertex_map WHERE id < 0
ORDER BY id DESC;
 id  | original_id
-----+-------------
  -1 |           6
  -2 |           7
  -3 |           7
  -4 |           7
  -5 |           7
  -6 |           7
  -7 |           7
  -8 |           7
  -9 |           3
 -10 |          11
 -11 |           8
(11 rows)

Adding a soft restriction ¶

A soft restriction going from vertex 6 to vertex 3 using edges 4 -> 7 is wanted.

Idenifying the restriction ¶

Running a pgr_dijkstraNear - Propuesto the edge with cost 0, edge 8, is where the cost will be increased

SELECT seq, path_seq, start_vid, end_vid, node, original_id, edge, cost, agg_cost
FROM (SELECT * FROM pgr_dijkstraNear(
  $$SELECT * FROM lineGraph_edges$$,
  (SELECT array_agg(id) FROM vertex_map where original_id = 6),
  (SELECT array_agg(id) FROM vertex_map where original_id = 3))) dn
JOIN vertex_map AS v1 ON (node = v1.id);
 seq | path_seq | start_vid | end_vid | node | original_id | edge | cost | agg_cost
-----+----------+-----------+---------+------+-------------+------+------+----------
   3 |        3 |        -1 |       3 |   -3 |           7 |    4 |    1 |        1
   1 |        1 |        -1 |       3 |   -1 |           6 |    1 |    1 |        0
   4 |        4 |        -1 |       3 |    3 |           3 |   -1 |    0 |        2
   2 |        2 |        -1 |       3 |    7 |           7 |    8 |    0 |        1
(4 rows)

The edge to be altered is WHERE cost = 0 AND seq != 1 AND edge != -1 from the previus query:

SELECT edge FROM pgr_dijkstraNear(
  $$SELECT * FROM lineGraph_edges$$,
  (SELECT array_agg(id) FROM vertex_map where original_id = 6),
  (SELECT array_agg(id) FROM vertex_map where original_id = 3))
WHERE cost = 0 AND seq != 1 AND edge != -1;
 edge
------
    8
(1 row)

Adding a value to the restriction ¶

Updating the cost to the edge:

UPDATE lineGraph_edges
SET cost = 100
WHERE id IN (
SELECT edge FROM pgr_dijkstraNear(
  $$SELECT * FROM lineGraph_edges$$,
  (SELECT array_agg(id) FROM vertex_map where original_id = 6),
  (SELECT array_agg(id) FROM vertex_map where original_id = 3))
WHERE cost = 0 AND seq != 1 AND edge != -1);
UPDATE 1

Ejemplo:: Routing from \(6\) to \(3\)

Now the route does not use edge 8 and does a U turn on a leaf vertex.

WITH
results AS (
  SELECT * FROM pgr_dijkstraNear(
    $$SELECT * FROM lineGraph_edges$$,
    (SELECT array_agg(id) FROM vertex_map where original_id = 6),
    (SELECT array_agg(id) FROM vertex_map where original_id = 3)))
SELECT seq, path_seq, start_vid, end_vid, node, original_id, edge, cost, agg_cost
FROM results
LEFT JOIN vertex_map AS v1 ON (node = v1.id) ORDER BY seq;
 seq | path_seq | start_vid | end_vid | node | original_id | edge | cost | agg_cost
-----+----------+-----------+---------+------+-------------+------+------+----------
   1 |        1 |        -1 |       3 |   -1 |           6 |    1 |    1 |        0
   2 |        2 |        -1 |       3 |    7 |           7 |   10 |    0 |        1
   3 |        3 |        -1 |       3 |   -5 |           7 |    6 |    1 |        1
   4 |        4 |        -1 |       3 |    8 |           8 |   28 |    0 |        2
   5 |        5 |        -1 |       3 |  -11 |           8 |   27 |    1 |        2
   6 |        6 |        -1 |       3 |   -8 |           7 |   20 |    0 |        3
   7 |        7 |        -1 |       3 |   -3 |           7 |    4 |    1 |        3
   8 |        8 |        -1 |       3 |    3 |           3 |   -1 |    0 |        4
(8 rows)

Simplifying leaf vertices ¶

In this example, there is no additional cost for traversing a leaf vertex.

Using the vertex map give the leaf verices their original value.¶

On the source column

WITH
u_turns AS (
SELECT e.id AS eid, v1.original_id
FROM linegraph_edges as e
JOIN vertex_map AS v1 ON (source = v1.id)
AND v1.original_id IN (3, 6, 8, 11))
UPDATE lineGraph_edges
SET source = original_id
FROM u_turns
WHERE id = eid;
UPDATE 8

On the target column

WITH
u_turns AS (
SELECT e.id AS eid, v1.original_id
FROM linegraph_edges as e
JOIN vertex_map AS v1 ON (target = v1.id)
AND v1.original_id IN (3, 6, 8, 11))
UPDATE lineGraph_edges
SET target = original_id
FROM u_turns
WHERE id = eid;
UPDATE 8

Removing self loops on leaf nodes ¶

The self loops of the leaf nodes are

SELECT * FROM linegraph_edges
WHERE source = target
ORDER BY id;
 id | source | target | cost | edge
----+--------+--------+------+------
  2 |      6 |      6 |    0 |    0
 24 |      3 |      3 |    0 |    0
 26 |     11 |     11 |    0 |    0
 28 |      8 |      8 |    0 |    0
(4 rows)

Which can be removed

DELETE FROM linegraph_edges
WHERE source = target;
DELETE 4

Ejemplo:: Routing from \(6\) to \(3\)

Routing can be done now using the original vertices id using pgr_dijkstra

WITH
results AS (
  SELECT * FROM pgr_dijkstra(
    $$SELECT * FROM lineGraph_edges$$, 6, 3))
SELECT seq, path_seq, node, original_id, edge, cost, agg_cost
FROM results
LEFT JOIN vertex_map AS v1 ON (node = v1.id) ORDER BY seq;
 seq | path_seq | node | original_id | edge | cost | agg_cost
-----+----------+------+-------------+------+------+----------
   1 |        1 |    6 |           6 |    1 |    1 |        0
   2 |        2 |    7 |           7 |    9 |    0 |        1
   3 |        3 |   -4 |           7 |    5 |    1 |        1
   4 |        4 |   11 |          11 |   25 |    1 |        2
   5 |        5 |   -7 |           7 |   16 |    0 |        3
   6 |        6 |   -3 |           7 |    4 |    1 |        3
   7 |        7 |    3 |           3 |   -1 |    0 |        4
(7 rows)

Complete routing graph ¶

Add edges from the original graph ¶

Add all the edges that are not involved in the line graph process to the new table

SELECT id, source, target, cost, reverse_cost
INTO new_graph from edges
WHERE id NOT IN (4, 7, 8, 10);
SELECT 14

Some administrative tasks to get new identifiers for the edges

CREATE SEQUENCE new_graph_id_seq;
CREATE SEQUENCE
ALTER TABLE new_graph ALTER COLUMN id SET DEFAULT nextval('new_graph_id_seq');
ALTER TABLE
ALTER TABLE new_graph ALTER COLUMN id SET NOT NULL;
ALTER TABLE
ALTER SEQUENCE new_graph_id_seq OWNED BY new_graph.id;
ALTER SEQUENCE
SELECT setval('new_graph_id_seq', (SELECT max(id) FROM new_graph));
 setval
--------
     18
(1 row)

Add the newly calculated edges ¶

INSERT INTO new_graph (source, target, cost, reverse_cost)
SELECT source, target, cost, -1 FROM lineGraph_edges;
INSERT 0 24

Using the routing graph ¶

When using this method for routing with soft restrictions there will be uturns

Ejemplo:: Routing from \(6\) to \(3\)

WITH
results AS (
  SELECT * FROM pgr_dijkstra(
    $$SELECT * FROM new_graph$$, 6, 3))
SELECT seq, path_seq, node, original_id, edge, cost, agg_cost
FROM results
LEFT JOIN vertex_map AS v1 ON (node = v1.id) ORDER BY seq;
 seq | path_seq | node | original_id | edge | cost | agg_cost
-----+----------+------+-------------+------+------+----------
   1 |        1 |    6 |           6 |   35 |    1 |        0
   2 |        2 |    7 |           7 |   20 |    0 |        1
   3 |        3 |   -4 |           7 |   41 |    1 |        1
   4 |        4 |   11 |          11 |   37 |    1 |        2
   5 |        5 |   -7 |           7 |   27 |    0 |        3
   6 |        6 |   -3 |           7 |   40 |    1 |        3
   7 |        7 |    3 |           3 |   -1 |    0 |        4
(7 rows)

Ejemplo:: Routing from \(5\) to \(1\)

WITH
results AS (
  SELECT * FROM pgr_dijkstra(
    $$SELECT * FROM new_graph$$, 5, 1))
SELECT seq, path_seq, node, original_id, edge, cost, agg_cost
FROM results
LEFT JOIN vertex_map AS v1 ON (node = v1.id) ORDER BY seq;
 seq | path_seq | node | original_id | edge | cost | agg_cost
-----+----------+------+-------------+------+------+----------
   1 |        1 |    5 |           5 |    1 |    1 |        0
   2 |        2 |    6 |           6 |   35 |    1 |        1
   3 |        3 |    7 |           7 |   20 |    0 |        2
   4 |        4 |   -4 |           7 |   41 |    1 |        2
   5 |        5 |   11 |          11 |   37 |    1 |        3
   6 |        6 |   -7 |           7 |   27 |    0 |        4
   7 |        7 |   -3 |           7 |   40 |    1 |        4
   8 |        8 |    3 |           3 |    6 |    1 |        5
   9 |        9 |    1 |           1 |   -1 |    0 |        6
(9 rows)

Ver también¶

Índices y tablas

pgr_lineGraphFull - Experimental¶

Descripción¶

Firmas¶

Parámetros¶

Consultas Internas¶

SQL aristas¶

Columnas de Resultados¶

Ejemplos Adicionales¶

Ver también¶

`pgr_lineGraphFull` - Experimental¶