收缩 - 函数族

• pgr_contraction

介绍

在大型图中，例如道路图或电网，图收缩可用于加速某些图算法。 收缩通过删除一些顶点和边来减小图的大小，例如，可能会添加表示原始边序列的边，从而减少图算法中使用的总时间和空间。

该实现为将来添加收缩算法提供了灵活的框架，目前它支持两种算法：

1. 死端收缩

2. 线性收缩

允许用户：

• 禁止在一组节点上收缩。

• 决定收缩算法的顺序并设置它们要执行的最大次数。

死端收缩

图的叶节点的收缩。

死端

当一个节点被认为是 死端 节点时

• 在无向图上：

  • 相邻顶点的个数为1。

• 在有向图上：

  • 相邻顶点的个数为1。

  • 没有传出边缘，但至少有一个传入边缘。

  • 没有传入边缘，但至少有一个传出边缘。

当条件成立时，可以进行当条件成立时，可以进行 操作: 死端收缩 。

无向图上的死端顶点

• 绿色节点是 死端 节点

• 蓝色节点具有无限数量的边。

节点	相邻节点	相邻节点数
\(a\)	\(\{u\}\)	1
\(b\)	\(\{v\}\)	1

有向图上的死端顶点

• 绿色节点是 死端 节点

• 蓝色节点具有无限数量的传入和/或传出边缘。

节点	相邻节点	相邻节点数	传入边数	传出边数
\(a\)	\(\{u\}\)	1
\(b\)	\(\{v\}\)	1
\(c\)	\(\{v, w\}\)	2	2	0
\(d\)	\(\{x\}\)	1
\(e\)	\(\{x, y\}\)	2	0	2

从上面来看，节点 \(\{a, b, d\}\) 是死端，因为相邻顶点的数量为 1。不需要对这些节点进行进一步检查。

下表中，节点 \(\{c, e\}\) 因为相邻顶点数不为1的偶数为

• \(c\)

  • 没有传出边缘，但至少有一个传入边缘。

• \(e\)

  • 没有传入边缘，但至少有一个传出边缘。

操作：死端收缩

死端收缩将停止，直到不再有死端节点。 例如，从下图中，其中 \(w\) 是 死端 节点：

收缩 \(w\) 后，节点 \(v\) 现在是一个 死端 节点并且已收缩：

在收缩 \(v\) 之后，停止。节点 \(u\) 有已收缩节点的信息。

节点 \(u\) 有已收缩节点的信息。

线性收缩

算法中，线性收缩用2表示。

线性

在无向图的情况下，当满足以下条件时，节点被视为`线性`节点

• 相邻顶点的数量为2。

在有向图的情况下，当满足以下条件时，节点被视为`线性`节点

• 相邻顶点的数量为2。

• 线性是对称的

无向图上的线性顶点

• 绿色节点是 线性 节点

• 蓝色节点具有无限数量的传入和传出边缘。

无向

节点	相邻节点	相邻节点数
\(v\)	\(\{u, w\}\)	2

有向图上的线性顶点

• 绿色节点是 线性 节点

• 蓝色节点具有无限数量的传入和传出边缘。

• 白色节点不是线性的，因为线性不对称。

  • 它是可能去走 \(y \rightarrow c \rightarrow z\)

  • 不可能走 \(z \rightarrow c \rightarrow y\)

节点	相邻节点	相邻节点数	是对称的吗？
\(a\)	\(\{u, v\}\)	2	是
\(b\)	\(\{w, x\}\)	2	是
\(c\)	\(\{y, z\}\)	2	否

操作：线性收缩

当不再有线性节点时，线性收缩将停止。 例如，在下图中，其中 \(v\) 和 \(w\) 是 线性 节点：

收缩 \(w\)，

• 顶点 \(w\) 已从图中移除

• 从图中删除边 \(v \rightarrow w\) 和 \(w \rightarrow z\)。

• 插入一条新边 \(v \rightarrow z\)，以红色表示。

收缩 \(v\)：

• 顶点 \(v\) 已从图中移除

• 从图中删除边 \(u \rightarrow v\) 和 \(v \rightarrow z\)。

• 插入一条新边 \(u \rightarrow z\)，以红色表示。

边 \(u \rightarrow z\) 有收缩点的信息。

循环

收缩一张图可以通过多个操作来完成。 操作的顺序会影响生成的收缩图，在应用一个操作后，可以由另一操作收缩的顶点集会发生变化。

此实现通过 operations_order``循环 ``max_cycles 次。

<input>
do max_cycles times {
    for (operation in operations_order)
     { do operation }
}
<output>

收缩示例数据

在本节中，将通过示例展示构建和使用收缩图。

• 使用无向图的 示例数据

• 首先是死端操作，然后是线性操作。

数据库中图的构建

原始数据

以下查询显示了收缩操作所涉及的原始数据。

SELECT id, source, target, cost, reverse_cost
FROM edges ORDER BY id;
 id | source | target | cost | reverse_cost
----+--------+--------+------+--------------
  1 |      5 |      6 |    1 |            1
  2 |      6 |     10 |   -1 |            1
  3 |     10 |     15 |   -1 |            1
  4 |      6 |      7 |    1 |            1
  5 |     10 |     11 |    1 |           -1
  6 |      1 |      3 |    1 |            1
  7 |      3 |      7 |    1 |            1
  8 |      7 |     11 |    1 |            1
  9 |     11 |     16 |    1 |            1
 10 |      7 |      8 |    1 |            1
 11 |     11 |     12 |    1 |           -1
 12 |      8 |     12 |    1 |           -1
 13 |     12 |     17 |    1 |           -1
 14 |      8 |      9 |    1 |            1
 15 |     16 |     17 |    1 |            1
 16 |     15 |     16 |    1 |            1
 17 |      2 |      4 |    1 |            1
 18 |     13 |     14 |    1 |            1
(18 rows)

原始图：

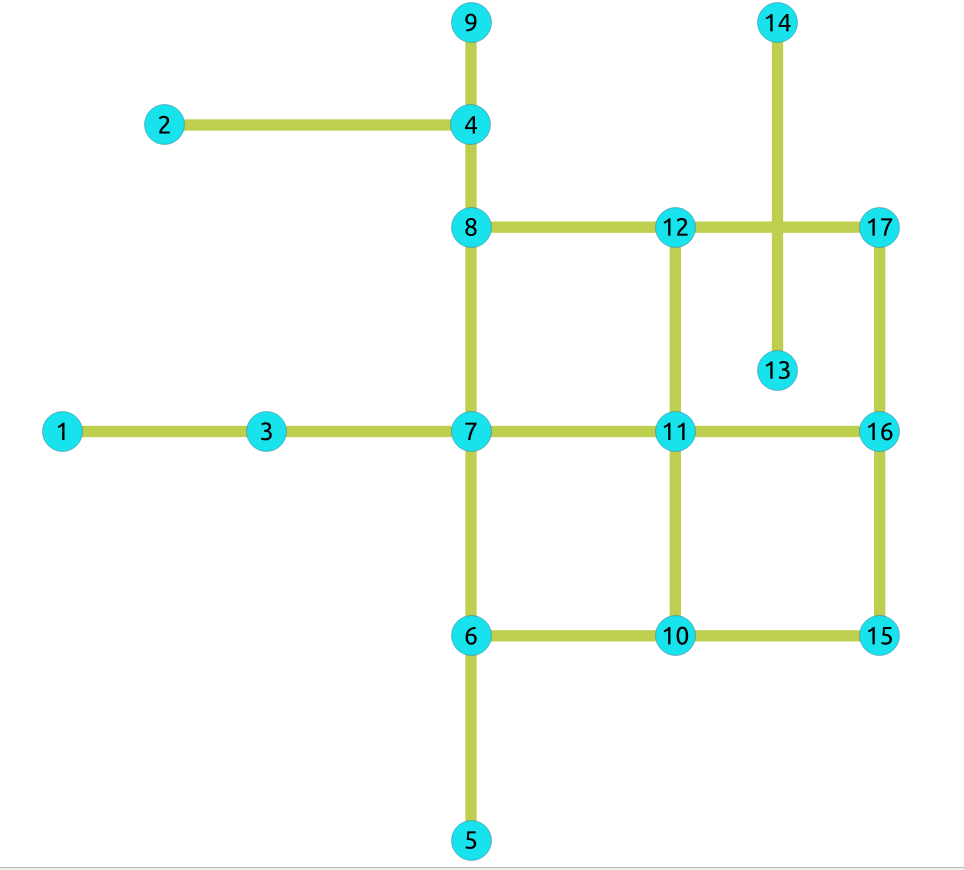
收缩结果

结果不代表收缩图。 它们表示应用收缩算法后对图所做的更改。

例如，观察到顶点 \(6\) 没有出现在结果中，因为它不受收缩算法的影响。

SELECT * FROM pgr_contraction(
  'SELECT id, source, target, cost, reverse_cost FROM edges',
  array[1, 2], directed => false);
 type | id | contracted_vertices | source | target | cost
------+----+---------------------+--------+--------+------
 v    |  4 | {2}                 |     -1 |     -1 |   -1
 v    |  7 | {1,3}               |     -1 |     -1 |   -1
 v    | 14 | {13}                |     -1 |     -1 |   -1
 e    | -1 | {5,6}               |      7 |     10 |    2
 e    | -2 | {8,9}               |      7 |     12 |    2
 e    | -3 | {17}                |     12 |     16 |    2
 e    | -4 | {15}                |     10 |     16 |    2
(7 rows)

进行死端收缩操作后：

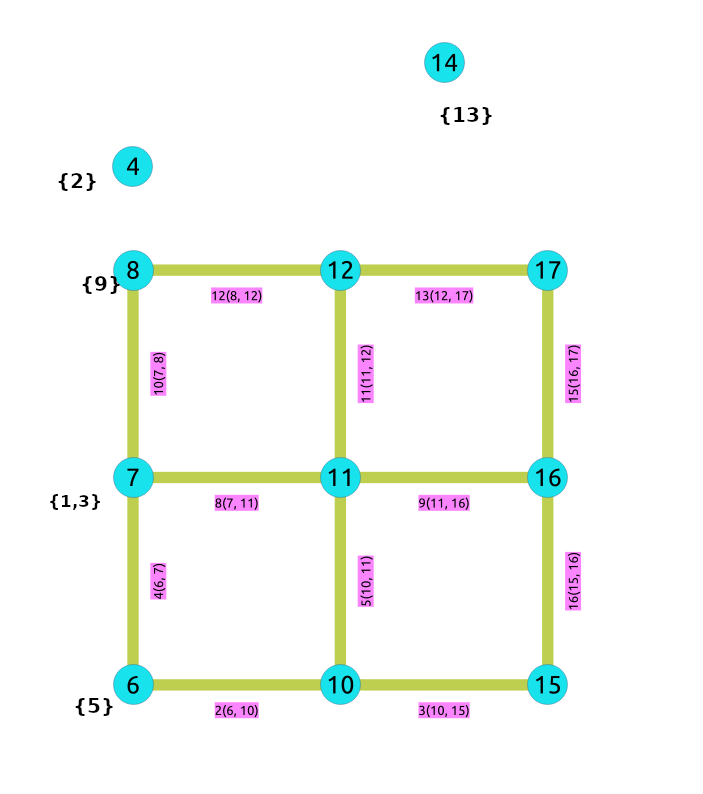
对上图进行线性收缩运算后：

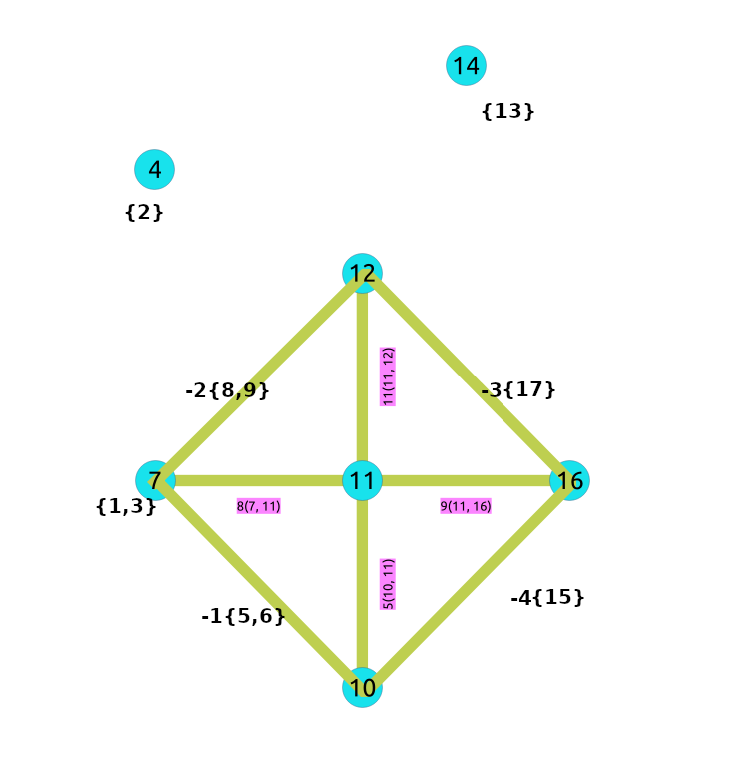
在数据库上创建收缩图的过程：

添加附加列

向 edge_table 和``edge_table_vertices_pgr`` 表添加额外的列，其中：

列	描述
contracted_vertices	属于顶点/边的顶点集
is_contracted	在顶点表上 当 true 时，顶点收缩，它不是收缩图的一部分。 当 false 时，顶点不收缩，它是收缩图的一部分。
is_new	在边表上 当 true 时，边缘由收缩算法生成。 它是收缩图的一部分。 当 false 时，边是原始边，可能是也可能不是收缩图的一部分。

ALTER TABLE vertices ADD is_contracted BOOLEAN DEFAULT false;
ALTER TABLE
ALTER TABLE vertices ADD contracted_vertices BIGINT[];
ALTER TABLE
ALTER TABLE edges ADD is_new BOOLEAN DEFAULT false;
ALTER TABLE
ALTER TABLE edges ADD contracted_vertices BIGINT[];
ALTER TABLE

存储收缩信息

将 收缩结果 存储在表中

SELECT * INTO contraction_results
FROM pgr_contraction(
  'SELECT id, source, target, cost, reverse_cost FROM edges',
  array[1, 2], directed => false);
SELECT 7

顶点表更新

使用 is_contracted 列来指示收缩的顶点。

UPDATE vertices
SET is_contracted = true
WHERE id IN (SELECT  unnest(contracted_vertices) FROM  contraction_results);
UPDATE 10

使用属于顶点的结果中的信息填充 contracted_vertices。

UPDATE vertices
SET contracted_vertices = contraction_results.contracted_vertices
FROM contraction_results
WHERE type = 'v' AND vertices.id = contraction_results.id;
UPDATE 3

修改后的顶点表：

SELECT id, contracted_vertices, is_contracted
FROM vertices
ORDER BY id;
 id | contracted_vertices | is_contracted
----+---------------------+---------------
  1 |                     | t
  2 |                     | t
  3 |                     | t
  4 | {2}                 | f
  5 |                     | t
  6 |                     | t
  7 | {1,3}               | f
  8 |                     | t
  9 |                     | t
 10 |                     | f
 11 |                     | f
 12 |                     | f
 13 |                     | t
 14 | {13}                | f
 15 |                     | t
 16 |                     | f
 17 |                     | t
(17 rows)

边缘表更新

插入由 pgr_contraction 生成的新边。

INSERT INTO edges(source, target, cost, reverse_cost, contracted_vertices, is_new)
SELECT source, target, cost, -1, contracted_vertices, true
FROM contraction_results
WHERE type = 'e';
INSERT 0 4

修改后的 edge_table。

SELECT id, source, target, cost, reverse_cost, contracted_vertices, is_new
FROM edges
ORDER BY id;
 id | source | target | cost | reverse_cost | contracted_vertices | is_new
----+--------+--------+------+--------------+---------------------+--------
  1 |      5 |      6 |    1 |            1 |                     | f
  2 |      6 |     10 |   -1 |            1 |                     | f
  3 |     10 |     15 |   -1 |            1 |                     | f
  4 |      6 |      7 |    1 |            1 |                     | f
  5 |     10 |     11 |    1 |           -1 |                     | f
  6 |      1 |      3 |    1 |            1 |                     | f
  7 |      3 |      7 |    1 |            1 |                     | f
  8 |      7 |     11 |    1 |            1 |                     | f
  9 |     11 |     16 |    1 |            1 |                     | f
 10 |      7 |      8 |    1 |            1 |                     | f
 11 |     11 |     12 |    1 |           -1 |                     | f
 12 |      8 |     12 |    1 |           -1 |                     | f
 13 |     12 |     17 |    1 |           -1 |                     | f
 14 |      8 |      9 |    1 |            1 |                     | f
 15 |     16 |     17 |    1 |            1 |                     | f
 16 |     15 |     16 |    1 |            1 |                     | f
 17 |      2 |      4 |    1 |            1 |                     | f
 18 |     13 |     14 |    1 |            1 |                     | f
 19 |      7 |     10 |    2 |           -1 | {5,6}               | t
 20 |      7 |     12 |    2 |           -1 | {8,9}               | t
 21 |     12 |     16 |    2 |           -1 | {17}                | t
 22 |     10 |     16 |    2 |           -1 | {15}                | t
(22 rows)

收缩图

属于收缩图的顶点。

SELECT id
FROM vertices
WHERE is_contracted = false
ORDER BY id;
 id
----
  4
  7
 10
 11
 12
 14
 16
(7 rows)

属于收缩图的边。

WITH
vertices_in_graph AS (
  SELECT id
  FROM vertices
  WHERE is_contracted = false
)
SELECT id, source, target, cost, reverse_cost, contracted_vertices
FROM edges
WHERE source IN (SELECT * FROM vertices_in_graph)
AND target IN (SELECT * FROM vertices_in_graph)
ORDER BY id;
 id | source | target | cost | reverse_cost | contracted_vertices
----+--------+--------+------+--------------+---------------------
  5 |     10 |     11 |    1 |           -1 |
  8 |      7 |     11 |    1 |            1 |
  9 |     11 |     16 |    1 |            1 |
 11 |     11 |     12 |    1 |           -1 |
 19 |      7 |     10 |    2 |           -1 | {5,6}
 20 |      7 |     12 |    2 |           -1 | {8,9}
 21 |     12 |     16 |    2 |           -1 | {17}
 22 |     10 |     16 |    2 |           -1 | {15}
(8 rows)

收缩图

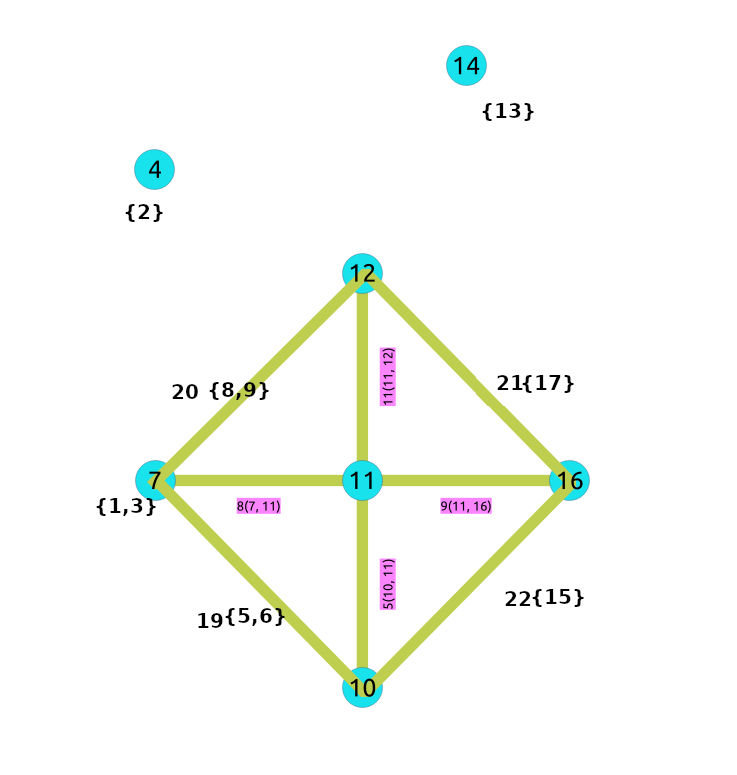
使用收缩图

将收缩图与 pgr_dijkstra 一起使用

计算收缩图中给定源和目标之间的最短路径时，存在三种情况：

• 情况1：源和目标都属于收缩图。

• 情况 2：源和/或目标属于边缘子图。

• 情况 3：源和/或目标属于一个顶点。

情况1：源和目标都属于收缩图。

使用 属于收缩图的边。 第 11 至 20 行。

CREATE OR REPLACE FUNCTION my_dijkstra(
  departure BIGINT, destination BIGINT,
  OUT seq INTEGER, OUT path_seq INTEGER,
  OUT start_vid BIGINT, OUT end_vid BIGINT,
  OUT node BIGINT, OUT edge BIGINT,
  OUT cost FLOAT, OUT agg_cost FLOAT)
RETURNS SETOF RECORD AS
$BODY$
SELECT * FROM pgr_dijkstra(
  $$
  WITH
  vertices_in_graph AS (
    SELECT id
    FROM vertices
    WHERE is_contracted = false
  )
  SELECT id, source, target, cost, reverse_cost
  FROM edges
  WHERE source IN (SELECT * FROM vertices_in_graph)
  AND target IN (SELECT * FROM vertices_in_graph)
  $$,
  departure, destination, false);
$BODY$
LANGUAGE SQL VOLATILE;
CREATE FUNCTION

情况1

当源和目标都属于收缩图时，就找到了一条路径。

SELECT * FROM my_dijkstra(10, 12);
 seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
   1 |        1 |        10 |      12 |   10 |    5 |    1 |        0
   2 |        2 |        10 |      12 |   11 |   11 |    1 |        1
   3 |        3 |        10 |      12 |   12 |   -1 |    0 |        2
(3 rows)

情况2

当源和/或目标属于边缘子图时，则找不到路径。

在这种情况下，收缩图没有与节点 \(4\) 相连的边。

SELECT * FROM my_dijkstra(15, 12);
 seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
(0 rows)

情况3

当源和/或目标属于顶点时，则找不到路径。

在这种情况下，收缩图没有与第二种情况的节点 \(7\) 和节点 \(4\) 连接的边。

SELECT * FROM my_dijkstra(15, 1);
 seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
(0 rows)

情况 2：源和/或目标属于边缘子图。

改进上述函数以包含属于边的节点。

• 需要扩展的顶点在第 11 至 17 行计算。

• 将第 26 至 28 行的附加部分添加到收缩图中。

CREATE OR REPLACE FUNCTION my_dijkstra(
  departure BIGINT, destination BIGINT,
  OUT seq INTEGER, OUT path_seq INTEGER,
  OUT start_vid BIGINT, OUT end_vid BIGINT,
  OUT node BIGINT, OUT edge BIGINT,
  OUT cost FLOAT, OUT agg_cost FLOAT)
RETURNS SETOF RECORD AS
$BODY$
SELECT * FROM pgr_dijkstra(
  $$
  WITH
  edges_to_expand AS (
    SELECT id
    FROM edges
    WHERE ARRAY[$$ || departure || $$]::BIGINT[] <@ contracted_vertices
    OR ARRAY[$$ || destination || $$]::BIGINT[] <@ contracted_vertices
  ),

  vertices_in_graph AS (
    SELECT id
    FROM vertices
    WHERE is_contracted = false

    UNION

    SELECT unnest(contracted_vertices)
    FROM edges
    WHERE id IN (SELECT id FROM edges_to_expand)
  )

  SELECT id, source, target, cost, reverse_cost
  FROM edges
  WHERE source IN (SELECT * FROM vertices_in_graph)
  AND target IN (SELECT * FROM vertices_in_graph)
  $$,
  departure, destination, false);
$BODY$
LANGUAGE SQL VOLATILE;
CREATE FUNCTION

情况1

当源和目标都属于收缩图时，就找到了一条路径。

SELECT * FROM my_dijkstra(10, 12);
 seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
   1 |        1 |        10 |      12 |   10 |    5 |    1 |        0
   2 |        2 |        10 |      12 |   11 |   11 |    1 |        1
   3 |        3 |        10 |      12 |   12 |   -1 |    0 |        2
(3 rows)

情况2

当源和目标都属于收缩图时，就找到了一条路径。

路由图现在有一条与节点 \(4\) 连接的边。

SELECT * FROM my_dijkstra(15, 12);
 seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
   1 |        1 |        15 |      12 |   15 |   16 |    1 |        0
   2 |        2 |        15 |      12 |   16 |   21 |    2 |        1
   3 |        3 |        15 |      12 |   12 |   -1 |    0 |        3
(3 rows)

情况3

当源和/或目标属于顶点时，则找不到路径。

在这种情况下，收缩图没有与节点 \(7\) 相连的边。

SELECT * FROM my_dijkstra(15, 1);
 seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
(0 rows)

情况 3：源和/或目标属于一个顶点。

改进上述函数以包含属于边的节点。

• 需要扩展的顶点在第19到24行计算。

• 将第 38 至 40 行的附加部分添加到收缩图中。

CREATE OR REPLACE FUNCTION my_dijkstra(
  departure BIGINT, destination BIGINT,
  OUT seq INTEGER, OUT path_seq INTEGER,
  OUT start_vid BIGINT, OUT end_vid BIGINT,
  OUT node BIGINT, OUT edge BIGINT,
  OUT cost FLOAT, OUT agg_cost FLOAT)
RETURNS SETOF RECORD AS
$BODY$
SELECT * FROM pgr_dijkstra(
  $$
  WITH
  edges_to_expand AS (
    SELECT id
    FROM edges
    WHERE ARRAY[$$ || departure || $$]::BIGINT[] <@ contracted_vertices
    OR ARRAY[$$ || destination || $$]::BIGINT[] <@ contracted_vertices
  ),

  vertices_to_expand AS (
    SELECT id
    FROM vertices
    WHERE ARRAY[$$ || departure || $$]::BIGINT[] <@ contracted_vertices
    OR ARRAY[$$ || destination || $$]::BIGINT[] <@ contracted_vertices
  ),

  vertices_in_graph AS (
    SELECT id
    FROM vertices
    WHERE is_contracted = false

    UNION

    SELECT unnest(contracted_vertices)
    FROM edges
    WHERE id IN (SELECT id FROM edges_to_expand)

    UNION

    SELECT unnest(contracted_vertices)
    FROM vertices
    WHERE id IN (SELECT id FROM vertices_to_expand)
  )

  SELECT id, source, target, cost, reverse_cost
  FROM edges
  WHERE source IN (SELECT * FROM vertices_in_graph)
  AND target IN (SELECT * FROM vertices_in_graph)
  $$,
  departure, destination, false);
$BODY$
LANGUAGE SQL VOLATILE;
CREATE FUNCTION

情况1

当源和目标都属于收缩图时，就找到了一条路径。

SELECT * FROM my_dijkstra(10, 12);
 seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
   1 |        1 |        10 |      12 |   10 |    5 |    1 |        0
   2 |        2 |        10 |      12 |   11 |   11 |    1 |        1
   3 |        3 |        10 |      12 |   12 |   -1 |    0 |        2
(3 rows)

情况2

代码更改不会影响这种情况，因此当源和/或目标属于边缘子图时，仍然会找到路径。

SELECT * FROM my_dijkstra(15, 12);
 seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
   1 |        1 |        15 |      12 |   15 |   16 |    1 |        0
   2 |        2 |        15 |      12 |   16 |   21 |    2 |        1
   3 |        3 |        15 |      12 |   12 |   -1 |    0 |        3
(3 rows)

情况3

当源和/或目标属于一个顶点时，现在就找到了一条路径。

现在，路由图有一条与节点 \(7\) 连接的边。

SELECT * FROM my_dijkstra(15, 1);
 seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
   1 |        1 |        15 |       1 |   15 |    3 |    1 |        0
   2 |        2 |        15 |       1 |   10 |   19 |    2 |        1
   3 |        3 |        15 |       1 |    7 |    7 |    1 |        3
   4 |        4 |        15 |       1 |    3 |    6 |    1 |        4
   5 |        5 |        15 |       1 |    1 |   -1 |    0 |        5
(5 rows)

另请参阅

• pgr_contraction

• 示例数据

• https://www.cs.cmu.edu/afs/cs/academic/class/15210-f12/www/lectures/lecture16.pdf

• https://algo2.iti.kit.edu/documents/routeplanning/geisberger_dipl.pdf

索引和表格

• Index

• Search Page