pgrouting::contraction::Pgr_linear< G > Class Template Reference

#include "pgr_linearContraction.hpp"

Collaboration diagram for pgrouting::contraction::Pgr_linear< G >:

Public Member Functions
	Pgr_linear ()
void	calculateVertices (G &graph)
void	doContraction (G &graph, Identifiers< V > forbidden_vertices)
bool	is_contractible (G &graph, V v)
void	one_cycle (G &graph, V v)
void	operator() (G &graph, Identifiers< V > &forbidden_vertices)
void	process_shortcut (G &graph, V u, V v, V w)
	u -—e1{v1}-—> v -—e2{v2}-—> w More...
void	setForbiddenVertices (Identifiers< V > forbidden_vertices)

Private Types
typedef G::B_G	B_G
typedef G::V	V
typedef G::V_i	V_i

Private Member Functions
int64_t	get_next_id ()

Private Attributes
int64_t	last_edge_id
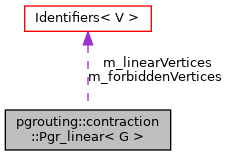
Identifiers< V >	m_forbiddenVertices
Identifiers< V >	m_linearVertices

Detailed Description

template<class G>
class pgrouting::contraction::Pgr_linear< G >

Definition at line 49 of file pgr_linearContraction.hpp.

Member Typedef Documentation

B_G

template<class G >

typedef G::B_G pgrouting::contraction::Pgr_linear< G >::B_G

private

Definition at line 53 of file pgr_linearContraction.hpp.

V

template<class G >

typedef G::V pgrouting::contraction::Pgr_linear< G >::V

private

Definition at line 51 of file pgr_linearContraction.hpp.

V_i

template<class G >

typedef G::V_i pgrouting::contraction::Pgr_linear< G >::V_i

private

Definition at line 52 of file pgr_linearContraction.hpp.

Constructor & Destructor Documentation

Pgr_linear()

template<class G >

pgrouting::contraction::Pgr_linear< G >::Pgr_linear ( )

inline

Definition at line 61 of file pgr_linearContraction.hpp.

:last_edge_id(0) {}

Member Function Documentation

calculateVertices()

template<class G >

void pgrouting::contraction::Pgr_linear< G >::calculateVertices ( G &  graph )

inline

Definition at line 79 of file pgr_linearContraction.hpp.

                                      {
         m_linearVertices.clear();
         V_i vi;
         BGL_FORALL_VERTICES_T(v, graph.graph, B_G) {
             if (is_contractible(graph, v)) {
                 m_linearVertices += v;
             }
         }
     }

References Identifiers< T >::clear(), pgrouting::contraction::Pgr_linear< G >::is_contractible(), and pgrouting::contraction::Pgr_linear< G >::m_linearVertices.

Referenced by pgrouting::contraction::Pgr_linear< G >::doContraction().

doContraction()

template<class G >

void pgrouting::contraction::Pgr_linear< G >::doContraction ( G &  graph, Identifiers< V >  forbidden_vertices  )

inline

Definition at line 91 of file pgr_linearContraction.hpp.

                                                                     {
         m_forbiddenVertices = forbidden_vertices;
         calculateVertices(graph);
 
         while (!m_linearVertices.empty()) {
             V v = m_linearVertices.front();
             m_linearVertices -= v;
             pgassert(is_contractible(graph, v));
             one_cycle(graph, v);
         }
     }

References pgrouting::contraction::Pgr_linear< G >::calculateVertices(), Identifiers< T >::empty(), Identifiers< T >::front(), pgrouting::contraction::Pgr_linear< G >::is_contractible(), pgrouting::contraction::Pgr_linear< G >::m_forbiddenVertices, pgrouting::contraction::Pgr_linear< G >::m_linearVertices, pgrouting::contraction::Pgr_linear< G >::one_cycle(), and pgassert.

Referenced by pgrouting::contraction::Pgr_linear< G >::operator()().

get_next_id()

template<class G >

int64_t pgrouting::contraction::Pgr_linear< G >::get_next_id ( )

inlineprivate

Definition at line 64 of file pgr_linearContraction.hpp.

                           {
         return --last_edge_id;
     }

References pgrouting::contraction::Pgr_linear< G >::last_edge_id.

Referenced by pgrouting::contraction::Pgr_linear< G >::process_shortcut().

is_contractible()

template<class G >

bool pgrouting::contraction::Pgr_linear< G >::is_contractible ( G &  graph, V  v  )

inline

Definition at line 75 of file pgr_linearContraction.hpp.

                                         {
         return graph.is_linear(v) && !m_forbiddenVertices.has(v);
     }

References Identifiers< T >::has(), and pgrouting::contraction::Pgr_linear< G >::m_forbiddenVertices.

Referenced by pgrouting::contraction::Pgr_linear< G >::calculateVertices(), pgrouting::contraction::Pgr_linear< G >::doContraction(), and pgrouting::contraction::Pgr_linear< G >::one_cycle().

one_cycle()

template<class G >

void pgrouting::contraction::Pgr_linear< G >::one_cycle ( G &  graph, V  v  )

inline

Definition at line 103 of file pgr_linearContraction.hpp.

                                   {
         pgassert(is_contractible(graph, v));
 
         Identifiers<V> adjacent_vertices =
             graph.find_adjacent_vertices(v);
         pgassert(adjacent_vertices.size() == 2);
 
         V u = adjacent_vertices.front();
         adjacent_vertices.pop_front();
         V w = adjacent_vertices.front();
         adjacent_vertices.pop_front();
 
         pgassert(v != u);
         pgassert(v != w);
         pgassert(u != w);
 
         if (graph.is_directed()) {
             /*
              *  u --> v --> w
              */
             process_shortcut(graph, u, v, w);
             /*
              *  w --> v --> u
              */
             process_shortcut(graph, w, v, u);
 
         } else {
             pgassert(graph.is_undirected());
             /*
              * u - v - w
              */
             process_shortcut(graph, u, v, w);
         }
 
         graph[v].contracted_vertices().clear();
         boost::clear_vertex(v, graph.graph);
         m_linearVertices -= v;
 
         if (is_contractible(graph, u)) {
             one_cycle(graph, u);
         } else {
             m_linearVertices -= u;
         }
         if (is_contractible(graph, w)) {
             one_cycle(graph, w);
         } else {
             m_linearVertices -= w;
         }
     }

References Identifiers< T >::front(), pgrouting::contraction::Pgr_linear< G >::is_contractible(), pgrouting::contraction::Pgr_linear< G >::m_linearVertices, pgassert, Identifiers< T >::pop_front(), pgrouting::contraction::Pgr_linear< G >::process_shortcut(), and Identifiers< T >::size().

Referenced by pgrouting::contraction::Pgr_linear< G >::doContraction().

operator()()

template<class G >

void pgrouting::contraction::Pgr_linear< G >::operator() ( G &  graph, Identifiers< V > &  forbidden_vertices  )

inline

Definition at line 57 of file pgr_linearContraction.hpp.

                                                                   {
         doContraction(graph, forbidden_vertices);
     }

References pgrouting::contraction::Pgr_linear< G >::doContraction().

process_shortcut()

template<class G >

void pgrouting::contraction::Pgr_linear< G >::process_shortcut ( G &  graph, V  u, V  v, V  w  )

inline

u -—e1{v1}-—> v -—e2{v2}-—> w

e1: min cost edge from u to v e2: min cost edge from v to w

result: u —{v+v1+v2}—> w

Definition at line 166 of file pgr_linearContraction.hpp.

                                                    {
         auto e1 = graph.get_min_cost_edge(u, v);
         auto e2 = graph.get_min_cost_edge(v, w);
 
         if (std::get<2>(e1) && std::get<2>(e2)) {
             auto contracted_vertices = std::get<1>(e1) + std::get<1>(e2);
             double cost = std::get<0>(e1) + std::get<0>(e2);
             contracted_vertices += graph[v].id;
             contracted_vertices += graph[v].contracted_vertices();
 
             // Create shortcut
             CH_edge shortcut(
                     get_next_id(),
                     graph[u].id,
                     graph[w].id,
                     cost);
             shortcut.contracted_vertices() = contracted_vertices;
 
             graph.add_shortcut(shortcut, u, w);
         }
     }

References pgrouting::CH_edge::contracted_vertices(), and pgrouting::contraction::Pgr_linear< G >::get_next_id().

Referenced by pgrouting::contraction::Pgr_linear< G >::one_cycle().

setForbiddenVertices()

template<class G >

void pgrouting::contraction::Pgr_linear< G >::setForbiddenVertices ( Identifiers< V >  forbidden_vertices )

inline

Definition at line 70 of file pgr_linearContraction.hpp.

                                                {
         m_forbiddenVertices = forbidden_vertices;
     }

References pgrouting::contraction::Pgr_linear< G >::m_forbiddenVertices.

Member Data Documentation

last_edge_id

template<class G >

int64_t pgrouting::contraction::Pgr_linear< G >::last_edge_id

private

Definition at line 193 of file pgr_linearContraction.hpp.

Referenced by pgrouting::contraction::Pgr_linear< G >::get_next_id().

m_forbiddenVertices

template<class G >

Identifiers<V> pgrouting::contraction::Pgr_linear< G >::m_forbiddenVertices

private

Definition at line 191 of file pgr_linearContraction.hpp.

Referenced by pgrouting::contraction::Pgr_linear< G >::doContraction(), pgrouting::contraction::Pgr_linear< G >::is_contractible(), and pgrouting::contraction::Pgr_linear< G >::setForbiddenVertices().

m_linearVertices

template<class G >

Identifiers<V> pgrouting::contraction::Pgr_linear< G >::m_linearVertices

private

Definition at line 190 of file pgr_linearContraction.hpp.

Referenced by pgrouting::contraction::Pgr_linear< G >::calculateVertices(), pgrouting::contraction::Pgr_linear< G >::doContraction(), and pgrouting::contraction::Pgr_linear< G >::one_cycle().

---

The documentation for this class was generated from the following file:

• pgr_linearContraction.hpp