pgr_bipartite - Experimental¶
pgr_bipartite — Conjuntos disjuntos tal que ningun par de vertices en el mismo conjunto son adjacentes.
Advertencia
Posible bloqueo del servidor
Estas funciones pueden crear una caída del servidor
Advertencia
Funciones experimentales
No son oficialmente de la versión actual.
Es probable que oficialmente no formen parte de la siguiente versión:
Las funciones no podrían hacer uso de ANY-INTEGER ni ANY-NUMERICAL
El nombre puede cambiar.
La firma puede cambiar.
La funcionalidad puede cambiar.
Las pruebas de pgTap pueden faltar.
Posiblemente necesite codificación c/c++.
Puede carecer documentación.
Hay documentación que, en dado caso, podría ser necesario reescribir.
Puede ser necesario que los ejemplos de documentación se generen automáticamente.
Puede ser necesaria retroalimentación por parte de la comunidad.
Puede depender de una función propuesta de pgRouting
Podría depender de una función obsoleta de pgRouting
Disponibilidad
Versión 3.2.0
Nueva función experimental.
Descripción¶
Un grafo bipartito es un grafo con dos conjuntos de vértices que están conectados entre sí, pero no dentro de sí mismos. Un gráfico bipartito es posible si el color del gráfico es posible utilizando dos colores, de modo que los vértices de un conjunto se colorean con el mismo color.
Las características principales son:
El algoritmo solo funciona en un grafo no dirigido.
Los valores devueltos no están ordenados.
El algoritmo comprueba si el grafo es bipartito o no. Si es bipartito entonces devuelve el nodo junto con dos colores 0 y 1 que representan dos conjuntos diferentes.
Si el grafo no es bipartito, el algoritmo devuelve un conjunto vacío.
Tiempo de ejecución:
Firmas¶
(vertex_id, color_id)- Ejemplo:
Cuando el grafo es bi-partido
SELECT * FROM pgr_bipartite(
$$SELECT id, source, target, cost, reverse_cost FROM edges$$
) ORDER BY vertex_id;
vertex_id | color_id
-----------+----------
1 | 0
2 | 0
3 | 1
4 | 1
5 | 0
6 | 1
7 | 0
8 | 1
9 | 0
10 | 0
11 | 1
12 | 0
13 | 0
14 | 1
15 | 1
16 | 0
17 | 1
(17 rows)
Parámetros¶
Parámetro |
Tipo |
Descripción |
|---|---|---|
|
SQL de aristas descritas más adelante. |
Consultas Internas¶
SQL aristas¶
Columna |
Tipo |
x Defecto |
Descripción |
|---|---|---|---|
|
ENTEROS |
Identificador de la arista. |
|
|
ENTEROS |
Identificador del primer vértice de la arista. |
|
|
ENTEROS |
Identificador del segundo vértice de la arista. |
|
|
FLOTANTES |
Peso de la arista ( |
|
|
FLOTANTES |
-1 |
Peso de la arista (
|
Donde:
- ENTEROS:
SMALLINT,INTEGER,BIGINT- FLOTANTES:
SMALLINT,INTEGER,BIGINT,REAL,FLOAT
Columnas de resultados¶
Regresa el conjunto de (vertex_id, color_id)
Columna |
Tipo |
Descripción |
|---|---|---|
|
|
Identificador del vértice. |
|
|
Identificador del color del vértice.
|
Ejemplo Adicional¶
- Ejemplo:
El gráfico cíclico de longitud impar no puede ser bipartito.
La arista
INSERT INTO edges (source, target, cost, reverse_cost) VALUES
(5, 1, 1, 1);
INSERT 0 1
Aristas en azul representan un grafo de ciclo impar.
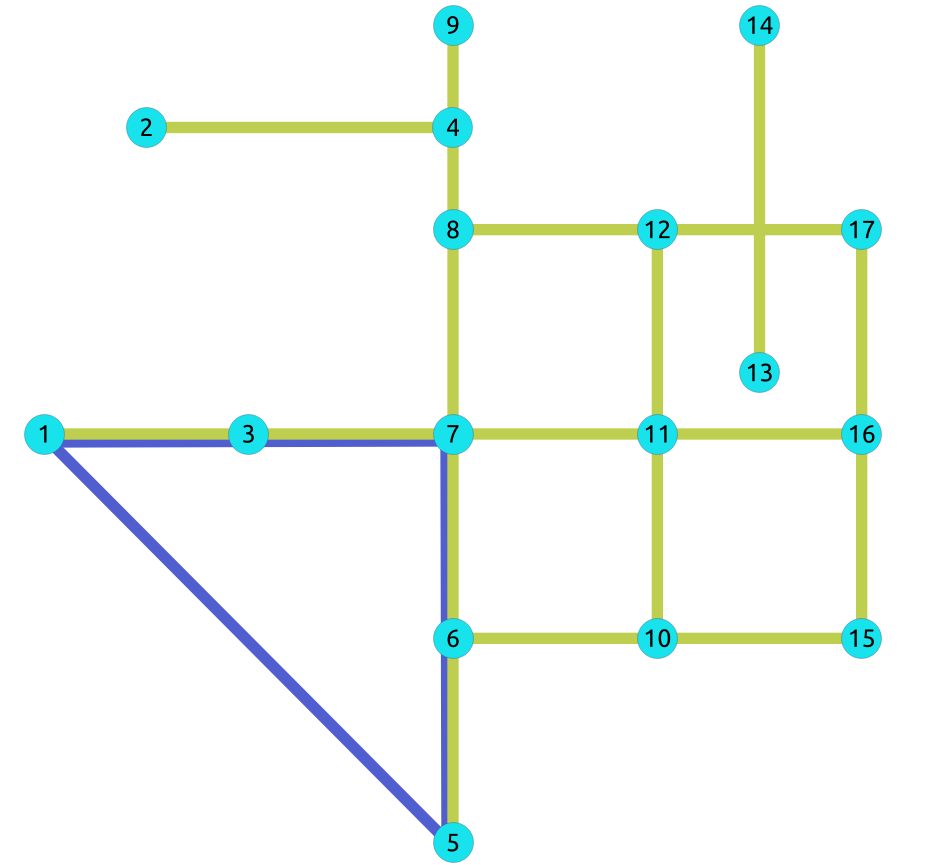
SELECT * FROM pgr_bipartite(
$$SELECT id, source, target, cost, reverse_cost FROM edges$$
);
vertex_id | color_id
-----------+----------
(0 rows)
Ver también¶
Índices y tablas
