pgrouting::graph::Pgr_lineGraph< G, T_V, T_E > Class Template Reference

#include "pgr_lineGraph.hpp"

Inheritance diagram for pgrouting::graph::Pgr_lineGraph< G, T_V, T_E >:

Collaboration diagram for pgrouting::graph::Pgr_lineGraph< G, T_V, T_E >:

Public Types
typedef boost::graph_traits< G >::edge_descriptor	E
typedef boost::graph_traits< G >::in_edge_iterator	EI_i
typedef boost::graph_traits< G >::out_edge_iterator	EO_i
typedef boost::graph_traits< G >::vertex_descriptor	V
typedef boost::graph_traits< G >::vertex_iterator	V_i

Public Member Functions
	Pgr_lineGraph (const pgrouting::DirectedGraph &digraph)
	Pgr_lineGraph (graphType gtype)
std::vector< Line_graph_rt >	get_postgres_results_directed ()
void	insert_vertices (const pgrouting::DirectedGraph &digraph)

Public Attributes
std::ostringstream	log

Private Member Functions
V	add_one_vertex (T_V vertex)
void	create_edges (const pgrouting::DirectedGraph &digraph)
template<typename T >
void	graph_add_edge (const T &source, const T &target)

Private Attributes
std::map< int64_t, pgr_edge_t >	m_edges

Friends
std::ostream &	operator<< (std::ostream &log, const Pgr_lineGraph< G, T_V, T_E > &g)

Graph related types
Type boost meaning pgRouting meaning G boost::adjacency_list Graph V vertex_descriptor Think of it as local ID of a vertex E edge_descriptor Think of it as local ID of an edge V_i vertex_iterator To cycle the vertices of the Graph E_i edge_iterator To cycle the edges of the Graph EO_i out_edge_iterator To cycle the out going edges of a vertex EI_i in_edge_iterator To cycle the in coming edges of a vertex (only in bidirectional graphs)
typedef G	B_G
typedef T_E	G_T_E
typedef T_V	G_T_V
typedef boost::graph_traits< G >::edge_iterator	E_i
typedef boost::graph_traits< G >::vertices_size_type	vertices_size_type
typedef boost::graph_traits< G >::edges_size_type	edges_size_type
typedef boost::graph_traits< G >::degree_size_type	degree_size_type

Id mapping handling
typedef std::map< V, size_t >	IndexMap
id_to_V	vertices_map
	id -> graph id More...
boost::property_map< G, boost::vertex_index_t >::type	vertIndex
IndexMap	mapIndex
boost::associative_property_map< IndexMap >	propmapIndex

Insert edges
template<typename T >
void	insert_edges (const T *edges, size_t count)
	Inserts count edges of type T into the graph. More...
template<typename T >
void	insert_edges (T *edges, size_t count, bool)
template<typename T >
void	insert_edges (const std::vector< T > &edges, bool normal=true)
	Inserts count edges of type pgr_edge_t into the graph The set of edges should not have an illegal vertex defined When the graph is empty calls: More...
template<typename T >
void	insert_edges_neg (const T *edges, size_t count)
template<typename T >
void	insert_negative_edges (const T *edges, int64_t count)
template<typename T >
void	insert_negative_edges (const std::vector< T > &edges, bool normal=true)
template<typename T >
void	insert_min_edges_no_parallel (const T *edges, size_t count)
template<typename T >
void	insert_min_edges_no_parallel (const std::vector< T > &edges)
void	add_vertices (std::vector< T_V > vertices)
	adds the vertices into the graph More...

Detailed Description

template<class G, typename T_V, typename T_E>
class pgrouting::graph::Pgr_lineGraph< G, T_V, T_E >

Definition at line 49 of file pgr_lineGraph.hpp.

Member Typedef Documentation

B_G

template<typename G , typename T_V , typename T_E >

typedef G pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::B_G

inherited

Definition at line 226 of file pgr_base_graph.hpp.

degree_size_type

template<typename G , typename T_V , typename T_E >

typedef boost::graph_traits< G >::degree_size_type pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::degree_size_type

inherited

Definition at line 241 of file pgr_base_graph.hpp.

E

template<class G , typename T_V , typename T_E >

typedef boost::graph_traits< G >::edge_descriptor pgrouting::graph::Pgr_lineGraph< G, T_V, T_E >::E

Definition at line 52 of file pgr_lineGraph.hpp.

E_i

template<typename G , typename T_V , typename T_E >

typedef boost::graph_traits< G >::edge_iterator pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::E_i

inherited

Definition at line 232 of file pgr_base_graph.hpp.

edges_size_type

template<typename G , typename T_V , typename T_E >

typedef boost::graph_traits< G >::edges_size_type pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::edges_size_type

inherited

Definition at line 239 of file pgr_base_graph.hpp.

EI_i

template<class G , typename T_V , typename T_E >

typedef boost::graph_traits< G >::in_edge_iterator pgrouting::graph::Pgr_lineGraph< G, T_V, T_E >::EI_i

Definition at line 55 of file pgr_lineGraph.hpp.

EO_i

template<class G , typename T_V , typename T_E >

typedef boost::graph_traits< G >::out_edge_iterator pgrouting::graph::Pgr_lineGraph< G, T_V, T_E >::EO_i

Definition at line 54 of file pgr_lineGraph.hpp.

G_T_E

template<typename G , typename T_V , typename T_E >

typedef T_E pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::G_T_E

inherited

Definition at line 227 of file pgr_base_graph.hpp.

G_T_V

template<typename G , typename T_V , typename T_E >

typedef T_V pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::G_T_V

inherited

Definition at line 228 of file pgr_base_graph.hpp.

id_to_V

template<typename G , typename T_V , typename T_E >

typedef std::map< int64_t, V > pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::id_to_V

inherited

Definition at line 253 of file pgr_base_graph.hpp.

IndexMap

template<typename G , typename T_V , typename T_E >

typedef std::map<V, size_t> pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::IndexMap

inherited

Definition at line 271 of file pgr_base_graph.hpp.

LI

template<typename G , typename T_V , typename T_E >

typedef id_to_V::const_iterator pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::LI

inherited

Definition at line 254 of file pgr_base_graph.hpp.

V

template<class G , typename T_V , typename T_E >

typedef boost::graph_traits< G >::vertex_descriptor pgrouting::graph::Pgr_lineGraph< G, T_V, T_E >::V

Definition at line 51 of file pgr_lineGraph.hpp.

V_i

template<class G , typename T_V , typename T_E >

typedef boost::graph_traits< G >::vertex_iterator pgrouting::graph::Pgr_lineGraph< G, T_V, T_E >::V_i

Definition at line 53 of file pgr_lineGraph.hpp.

vertices_size_type

template<typename G , typename T_V , typename T_E >

typedef boost::graph_traits< G >::vertices_size_type pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::vertices_size_type

inherited

Definition at line 237 of file pgr_base_graph.hpp.

Constructor & Destructor Documentation

Pgr_lineGraph() [1/2]

template<class G , typename T_V , typename T_E >

pgrouting::graph::Pgr_lineGraph< G, T_V, T_E >::Pgr_lineGraph ( graphType  gtype )

inlineexplicit

Definition at line 58 of file pgr_lineGraph.hpp.

        : Pgr_base_graph< G, T_V, T_E >(gtype) {
        }

Pgr_lineGraph() [2/2]

template<class G , typename T_V , typename T_E >

pgrouting::graph::Pgr_lineGraph< G, T_V, T_E >::Pgr_lineGraph ( const pgrouting::DirectedGraph &  digraph )

inlineexplicit

Definition at line 62 of file pgr_lineGraph.hpp.

        : Pgr_base_graph< G, T_V, T_E >(graphType::DIRECTED) {
            insert_vertices(digraph);
            create_edges(digraph);
        }

References pgrouting::graph::Pgr_lineGraph< G, T_V, T_E >::create_edges(), and pgrouting::graph::Pgr_lineGraph< G, T_V, T_E >::insert_vertices().

Member Function Documentation

add_one_vertex()

template<class G , typename T_V , typename T_E >

V pgrouting::graph::Pgr_lineGraph< G, T_V, T_E >::add_one_vertex ( T_V  vertex )

inlineprivate

Definition at line 202 of file pgr_lineGraph.hpp.

                        {
        auto v =  add_vertex(this->graph);
        this->vertices_map[vertex.id] = v;
        this->graph[v].cp_members(vertex);
 
        pgassert(boost::num_vertices(this->graph) == this->num_vertices());
        return v;
    }

References pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::graph, pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::num_vertices(), pgassert, and pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::vertices_map.

Referenced by pgrouting::graph::Pgr_lineGraph< G, T_V, T_E >::insert_vertices().

add_vertices()

template<typename G , typename T_V , typename T_E >

void pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::add_vertices ( std::vector< T_V >  vertices )

inlineprivateinherited

adds the vertices into the graph

PRECONDITIONS:

• The graph has not being initialized before
• There are no dupicated vertices

precondition(boost::num_vertices(graph) == 0);
for (vertex : vertices)
   precondition(!has_vertex(vertex.id));

POSTCONDITIONS:

postcondition(boost::num_vertices(graph) == vertices.size());
for (vertex : vertices)
   postcondition(has_vertex(vertex.id));

Example use:

pgrouting::DirectedGraph digraph(gType);
auto vertices(pgrouting::extract_vertices(data_edges, total_edges));
digraph.add_vertices(vertices);

Definition at line 462 of file pgr_base_graph.hpp.

                                        {
         pgassert(num_vertices() == 0);
         for (const auto vertex : vertices) {
             pgassert(!has_vertex(vertex.id));
 
             auto v =  add_vertex(graph);
             vertices_map[vertex.id] =  v;
             graph[v].cp_members(vertex);
             // put(propmapIndex, v, num_vertices());
 
             pgassert(has_vertex(vertex.id));
         }
         // pgassert(mapIndex.size() == vertices.size());
         pgassert(num_vertices() == vertices.size());
     }

Referenced by pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::insert_edges().

adjacent()

template<typename G , typename T_V , typename T_E >

V pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::adjacent ( V  v_idx, E  e_idx  ) const

inlineinherited

Definition at line 562 of file pgr_base_graph.hpp.

                                        {
         pgassert(is_source(v_idx, e_idx) || is_target(v_idx, e_idx));
         return is_source(v_idx, e_idx)?
             target(e_idx) :
             source(e_idx);
     }

Referenced by pgrouting::alphashape::Pgr_alphaShape::make_triangles().

create_edges()

template<class G , typename T_V , typename T_E >

void pgrouting::graph::Pgr_lineGraph< G, T_V, T_E >::create_edges ( const pgrouting::DirectedGraph &  digraph )

inlineprivate

Definition at line 169 of file pgr_lineGraph.hpp.

                                                   {
        V_i vertexIt, vertexEnd;
        EO_i e_outIt, e_outEnd;
        EI_i e_inIt, e_inEnd;
 
 
        /* for (each vertex v in original graph) */
        for (boost::tie(vertexIt, vertexEnd) = boost::vertices(digraph.graph);
                vertexIt != vertexEnd; vertexIt++) {
            auto vertex = *vertexIt;
 
           /* for( all incoming edges in to vertex v) */
            for (boost::tie(e_outIt, e_outEnd) =
                    boost::out_edges(vertex, digraph.graph);
                    e_outIt != e_outEnd;
                    e_outIt++) {
                /* for( all outgoing edges out from vertex v) */
                for (boost::tie(e_inIt, e_inEnd) =
                        boost::in_edges(vertex, digraph.graph);
                        e_inIt != e_inEnd; e_inIt++) {
                    /*
                       Prevent self-edges from being created in the Line Graph
                       */
 
                    graph_add_edge(
                            (digraph.graph[*e_inIt]).id,
                            (digraph.graph[*e_outIt]).id);
                }
            }
        }
    }

References pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::graph, and pgrouting::graph::Pgr_lineGraph< G, T_V, T_E >::graph_add_edge().

Referenced by pgrouting::graph::Pgr_lineGraph< G, T_V, T_E >::Pgr_lineGraph().

disconnect_edge()

template<class G , typename T_V , typename T_E >

void pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::disconnect_edge ( int64_t  p_from, int64_t  p_to  )

inherited

Disconnects all edges from p_from to p_to.

• No edge is disconnected if the vertices id's do not exist in the graph
• All removed edges are stored for future reinsertion
• All parallel edges are disconnected (automatically by boost)
  

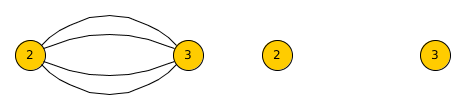
  disconnect_edge(2,3) on an UNDIRECTED graph

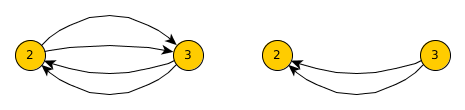
disconnect_edge(2,3) on a DIRECTED graph

Parameters

[in]	p_from	original vertex id of the starting point of the edge
[in]	p_to	original vertex id of the ending point of the edge

Definition at line 765 of file pgr_base_graph.hpp.

                                                                           {
    T_E d_edge;
 
    // nothing to do, the vertex doesn't exist
    if (!has_vertex(p_from) || !has_vertex(p_to)) return;
 
    EO_i out, out_end;
    V g_from(get_V(p_from));
    V g_to(get_V(p_to));
 
    // store the edges that are going to be removed
    for (boost::tie(out, out_end) = out_edges(g_from, graph);
            out != out_end; ++out) {
        if (target(*out) == g_to) {
            d_edge.id = graph[*out].id;
            d_edge.source = graph[source(*out)].id;
            d_edge.target = graph[target(*out)].id;
            d_edge.cost = graph[*out].cost;
            removed_edges.push_back(d_edge);
        }
    }
    // the actual removal
    boost::remove_edge(g_from, g_to, graph);
}

disconnect_out_going_edge()

template<class G , typename T_V , typename T_E >

void pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::disconnect_out_going_edge ( int64_t  vertex_id, int64_t  edge_id  )

inherited

Disconnects the outgoing edges of a vertex.

• No edge is disconnected if it doesn't exist in the graph
• Removed edges are stored for future reinsertion
• all outgoing edges with the edge_id are removed if they exist

  Parameters

  [in]	vertex_id	original vertex
  [in]	edge_id	original edge_id

Definition at line 794 of file pgr_base_graph.hpp.

                                            {
    T_E d_edge;
 
    // nothing to do, the vertex doesn't exist
    if (!has_vertex(vertex_id)) return;
    auto v_from(get_V(vertex_id));
 
    EO_i out, out_end;
    bool change = true;
    // store the edge that are going to be removed
    while (change) {
        change = false;
        for (boost::tie(out, out_end) = out_edges(v_from, graph);
                out != out_end; ++out) {
            if (graph[*out].id  == edge_id) {
                d_edge.id = graph[*out].id;
                d_edge.source = graph[source(*out)].id;
                d_edge.target = graph[target(*out)].id;
                d_edge.cost = graph[*out].cost;
                removed_edges.push_back(d_edge);
                boost::remove_edge((*out), graph);
                change = true;
                break;
            }
        }
    }
}

disconnect_vertex() [1/2]

template<class G , typename T_V , typename T_E >

void pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::disconnect_vertex ( int64_t  p_vertex )

inherited

Disconnects all incoming and outgoing edges from the vertex.

boost::graph doesn't recommend th to insert/remove vertices, so a vertex removal is simulated by disconnecting the vertex from the graph

• No edge is disconnected if the vertices id's do not exist in the graph
• All removed edges are stored for future reinsertion
• All parallel edges are disconnected (automatically by boost)
  

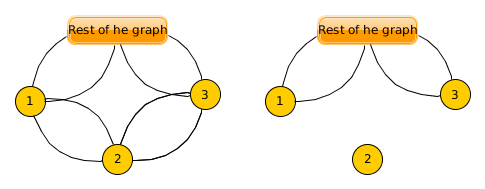
  disconnect_vertex(2) on an UNDIRECTED graph

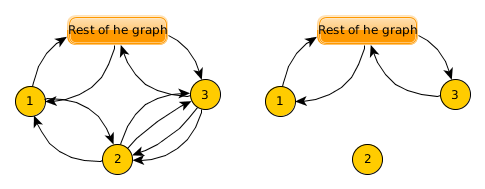
disconnect_vertex(2) on a DIRECTED graph

Parameters

[in]

p_vertex

original vertex id of the starting point of the edge

Definition at line 826 of file pgr_base_graph.hpp.

                                                               {
    if (!has_vertex(vertex)) return;
    disconnect_vertex(get_V(vertex));
}

disconnect_vertex() [2/2]

template<class G , typename T_V , typename T_E >

void pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::disconnect_vertex ( V  vertex )

inherited

Definition at line 833 of file pgr_base_graph.hpp.

                                                         {
    T_E d_edge;
 
    EO_i out, out_end;
    // store the edges that are going to be removed
    for (boost::tie(out, out_end) = out_edges(vertex, graph);
            out != out_end; ++out) {
        d_edge.id = graph[*out].id;
        d_edge.source = graph[source(*out)].id;
        d_edge.target = graph[target(*out)].id;
        d_edge.cost = graph[*out].cost;
        removed_edges.push_back(d_edge);
    }
 
    // special case
    if (m_gType == DIRECTED) {
        EI_i in, in_end;
        for (boost::tie(in, in_end) = in_edges(vertex, graph);
                in != in_end; ++in) {
            d_edge.id = graph[*in].id;
            d_edge.source = graph[source(*in)].id;
            d_edge.target = graph[target(*in)].id;
            d_edge.cost = graph[*in].cost;
            removed_edges.push_back(d_edge);
        }
    }
 
    // delete incoming and outgoing edges from the vertex
    boost::clear_vertex(vertex, graph);
}

get_edge()

template<typename G , typename T_V , typename T_E >

E pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::get_edge ( V  from, V  to, double &  distance  ) const

inlineinherited

Definition at line 671 of file pgr_base_graph.hpp.

                                     {
         E e;
         EO_i out_i, out_end;
         V v_source, v_target;
         double minCost =  (std::numeric_limits<double>::max)();
         E minEdge;
         bool valid = false;
         for (boost::tie(out_i, out_end) = boost::out_edges(from, graph);
                 out_i != out_end; ++out_i) {
             e = *out_i;
             if (!valid) {
                 minEdge = e;
                 valid = true;
             }
             v_target = target(e);
             v_source = source(e);
             if ((from == v_source) && (to == v_target)
                     && (distance == graph[e].cost)) {
                 return e;
             }
             if ((from == v_source) && (to == v_target)
                     && (minCost > graph[e].cost)) {
                 minCost = graph[e].cost;
                 minEdge = e;
             }
         }
         return minEdge;
     }

get_edge_id()

template<class G , typename T_V , typename T_E >

int64_t pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::get_edge_id ( V  from, V  to, double &  distance  ) const

inherited

Definition at line 878 of file pgr_base_graph.hpp.

                                {
    E e;
    EO_i out_i, out_end;
    V v_source, v_target;
    double minCost =  (std::numeric_limits<double>::max)();
    int64_t minEdge = -1;
    for (boost::tie(out_i, out_end) = boost::out_edges(from, graph);
            out_i != out_end; ++out_i) {
        e = *out_i;
        v_target = target(e);
        v_source = source(e);
        if ((from == v_source) && (to == v_target)
                && (distance == graph[e].cost))
            return graph[e].id;
        if ((from == v_source) && (to == v_target)
                && (minCost > graph[e].cost)) {
            minCost = graph[e].cost;
            minEdge = graph[e].id;
        }
    }
    distance = minEdge == -1? 0: minCost;
    return minEdge;
}

get_postgres_results_directed()

template<class G , typename T_V , typename T_E >

std::vector< Line_graph_rt > pgrouting::graph::Pgr_lineGraph< G, T_V, T_E >::get_postgres_results_directed ( )

inline

Definition at line 91 of file pgr_lineGraph.hpp.

                                        {
            std::vector< Line_graph_rt > results;
 
            typename boost::graph_traits < G >::edge_iterator edgeIt, edgeEnd;
            std::map < std::pair<int64_t, int64_t >, Line_graph_rt > unique;
            int64_t count = 0;
 
            for (boost::tie(edgeIt, edgeEnd) = boost::edges(this->graph);
                    edgeIt != edgeEnd; edgeIt++) {
                E e = *edgeIt;
                auto e_source = this->graph[this->source(e)].vertex_id;
                auto e_target = this->graph[this->target(e)].vertex_id;
 
                if (unique.find({e_target, e_source}) != unique.end()) {
                    unique[std::pair<int64_t, int64_t>(e_target,
                            e_source)].reverse_cost = 1.0;
                    continue;
                }
                e_source *= -1;
                e_target *= -1;
                if (unique.find({e_target, e_source}) != unique.end()) {
                    unique[std::pair<int64_t, int64_t>(e_target,
                            e_source)].reverse_cost = 1.0;
                    continue;
                }
                e_source *= -1;
                e_target *= -1;
 
                Line_graph_rt edge = {
                    ++count,
                    e_source,
                    e_target,
                    1.0,
                    -1.0
                };
                unique[std::pair<int64_t, int64_t>(e_source, e_target)] = edge;
            }
            for (const auto &edge : unique) {
                results.push_back(edge.second);
            }
            return results;
        }

References pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::graph, pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::source(), and pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::target().

get_V() [1/2]

template<typename G , typename T_V , typename T_E >

V pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::get_V ( const T_V &  vertex )

inlineinherited

get the vertex descriptor of the vertex When the vertex does not exist

• creates a new vetex

  Returns

  V: The vertex descriptor of the vertex

Definition at line 512 of file pgr_base_graph.hpp.

                                {
         auto vm_s(vertices_map.find(vertex.id));
         if (vm_s == vertices_map.end()) {
             auto v =  add_vertex(graph);
             graph[v].cp_members(vertex);
             vertices_map[vertex.id] =  v;
             put(propmapIndex, v, num_vertices());
             return v;
         }
         return vm_s->second;
     }

Referenced by pgrouting::graph::Pgr_lineGraph< G, T_V, T_E >::graph_add_edge(), pgrouting::graph::Pgr_lineGraphFull< G, T_V, T_E >::graph_add_edge(), pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::graph_add_edge_no_create_vertex(), pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::in_degree(), and pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::out_degree().

get_V() [2/2]

template<typename G , typename T_V , typename T_E >

V pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::get_V ( int64_t  vid ) const

inlineinherited

get the vertex descriptor of the vid Call has_vertex(vid) before calling this function

Returns

V: The vertex descriptor of the vertex

Definition at line 528 of file pgr_base_graph.hpp.

                                {
         pgassert(has_vertex(vid));
         return vertices_map.find(vid)->second;
     }

graph_add_edge() [1/3]

template<class G , typename T_V , typename T_E >

template<typename T >

void pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::graph_add_edge ( const T &  edge, bool  normal = true  )

inherited

Definition at line 936 of file pgr_base_graph.hpp.

                                                                        {
    bool inserted;
    typename Pgr_base_graph< G, T_V, T_E >::E e;
    if ((edge.cost < 0) && (edge.reverse_cost < 0))
        return;
 
    /*
     * true: for source
     * false: for target
     */
    auto vm_s = get_V(T_V(edge, true));
    auto vm_t = get_V(T_V(edge, false));
 
    pgassert(vertices_map.find(edge.source) != vertices_map.end());
    pgassert(vertices_map.find(edge.target) != vertices_map.end());
    if (edge.cost >= 0) {
        boost::tie(e, inserted) =
            boost::add_edge(vm_s, vm_t, graph);
        graph[e].cost = edge.cost;
        graph[e].id = edge.id;
    }
 
    if (edge.reverse_cost >= 0
            && (m_gType == DIRECTED
                || (m_gType == UNDIRECTED && edge.cost != edge.reverse_cost))) {
        boost::tie(e, inserted) =
            boost::add_edge(vm_t, vm_s, graph);
 
        graph[e].cost = edge.reverse_cost;
        graph[e].id = normal? edge.id : -edge.id;
    }
}

graph_add_edge() [2/3]

template<class G , typename T_V , typename T_E >

template<typename T >

void pgrouting::graph::Pgr_lineGraph< G, T_V, T_E >::graph_add_edge ( const T &  source, const T &  target  )

inlineprivate

Definition at line 154 of file pgr_lineGraph.hpp.

                                 {
            bool inserted;
            E e;
 
            auto vm_s = this->get_V(source);
            auto vm_t = this->get_V(target);
 
            boost::tie(e, inserted) =
                boost::add_edge(vm_s, vm_t, this->graph);
 
            this->graph[e].id = static_cast<int64_t>(this->num_edges());
        }

References pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::get_V(), pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::graph, and pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::num_edges().

Referenced by pgrouting::graph::Pgr_lineGraph< G, T_V, T_E >::create_edges().

graph_add_edge() [3/3]

template<class G , typename T_V , typename T_E >

void pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::graph_add_edge ( const T_E &  edge )

inherited

Definition at line 908 of file pgr_base_graph.hpp.

                                                              {
    typename Pgr_base_graph< G, T_V, T_E >::LI vm_s, vm_t;
    typename Pgr_base_graph< G, T_V, T_E >::E e;
 
    vm_s = vertices_map.find(edge.source);
    if (vm_s == vertices_map.end()) {
        vertices_map[edge.source]=  num_vertices();
        vm_s = vertices_map.find(edge.source);
    }
 
    vm_t = vertices_map.find(edge.target);
    if (vm_t == vertices_map.end()) {
        vertices_map[edge.target]=  num_vertices();
        vm_t = vertices_map.find(edge.target);
    }
 
    if (edge.cost >= 0) {
        bool inserted;
        boost::tie(e, inserted) =
            boost::add_edge(vm_s->second, vm_t->second, graph);
        graph[e].cp_members(edge);
    }
}

Referenced by pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::insert_edges().

graph_add_edge_no_create_vertex()

template<typename G , typename T_V , typename T_E >

template<typename T >

void pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::graph_add_edge_no_create_vertex ( const T &  edge )

inlineinherited

Use this function when the vertices are already inserted in the graph.

Definition at line 721 of file pgr_base_graph.hpp.

                                                         {
         bool inserted;
         E e;
         if ((edge.cost < 0) && (edge.reverse_cost < 0))
             return;
 
#if 0
         std::ostringstream log;
         for (auto iter = vertices_map.begin();
                 iter != vertices_map.end();
                 iter++) {
             log << "Key: " << iter->first <<"\tValue:" << iter->second << "\n";
         }
         pgassertwm(has_vertex(edge.source), log.str().c_str());
         pgassert(has_vertex(edge.target));
#endif
 
         auto vm_s = get_V(edge.source);
         auto vm_t = get_V(edge.target);
 
 
         if (edge.cost >= 0) {
             boost::tie(e, inserted) =
                 boost::add_edge(vm_s, vm_t, graph);
             graph[e].cost = edge.cost;
             graph[e].id = edge.id;
         }
 
 
         if (edge.reverse_cost >= 0 && (is_directed()
                     || (is_undirected() && edge.cost != edge.reverse_cost))) {
             boost::tie(e, inserted) =
                 boost::add_edge(vm_t, vm_s, graph);
             graph[e].cost = edge.reverse_cost;
             graph[e].id = edge.id;
         }
     }

Referenced by pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::insert_edges().

graph_add_min_edge_no_parallel()

template<class G , typename T_V , typename T_E >

template<typename T >

void pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::graph_add_min_edge_no_parallel ( const T &  edge )

inherited

Definition at line 972 of file pgr_base_graph.hpp.

                                                                           {
    bool inserted;
    typename Pgr_base_graph< G, T_V, T_E >::E e;
    if ((edge.cost < 0) && (edge.reverse_cost < 0))
        return;
 
    /*
     * true: for source
     * false: for target
     */
    auto vm_s = get_V(T_V(edge, true));
    auto vm_t = get_V(T_V(edge, false));
 
    pgassert(vertices_map.find(edge.source) != vertices_map.end());
    pgassert(vertices_map.find(edge.target) != vertices_map.end());
    if (edge.cost >= 0) {
        E e1;
        bool found;
        boost::tie(e1, found) = edge(vm_s, vm_t, graph);
        if (found) {
            if (edge.cost < graph[e1].cost) {
                graph[e1].cost = edge.cost;
                graph[e1].id = edge.id;
            }
        } else {
            boost::tie(e, inserted) =
                boost::add_edge(vm_s, vm_t, graph);
            graph[e].cost = edge.cost;
            graph[e].id = edge.id;
        }
    }
 
    if (edge.reverse_cost >= 0
            && (m_gType == DIRECTED
                || (m_gType == UNDIRECTED && edge.cost != edge.reverse_cost))) {
        E e1;
        bool found;
        boost::tie(e1, found) = edge(vm_t, vm_s, graph);
        if (found) {
            if (edge.reverse_cost < graph[e1].cost) {
                graph[e1].cost = edge.reverse_cost;
                graph[e1].id = edge.id;
            }
        } else {
            boost::tie(e, inserted) =
                boost::add_edge(vm_t, vm_s, graph);
 
            graph[e].cost = edge.reverse_cost;
            graph[e].id = edge.id;
        }
    }
}

Referenced by pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::insert_min_edges_no_parallel().

graph_add_neg_edge()

template<class G , typename T_V , typename T_E >

template<typename T >

void pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::graph_add_neg_edge ( const T &  edge, bool  normal = true  )

inherited

Definition at line 1035 of file pgr_base_graph.hpp.

                                                                            {
    bool inserted;
    typename Pgr_base_graph< G, T_V, T_E >::E e;
 
    auto vm_s = get_V(T_V(edge, true));
    auto vm_t = get_V(T_V(edge, false));
 
    pgassert(vertices_map.find(edge.source) != vertices_map.end());
    pgassert(vertices_map.find(edge.target) != vertices_map.end());
 
    boost::tie(e, inserted) =
            boost::add_edge(vm_s, vm_t, graph);
        if (edge.cost < 0) {
            // reading negative edges as positive
            graph[e].cost = (-0.5)*edge.cost;
        } else {
            graph[e].cost = edge.cost;
        }
        graph[e].id = edge.id;
 
    if (m_gType == DIRECTED
              || (m_gType == UNDIRECTED && edge.cost > edge.reverse_cost)) {
        boost::tie(e, inserted) =
            boost::add_edge(vm_t, vm_s, graph);
        if (edge.reverse_cost < 0) {
            // reading negative edges as positive
            graph[e].cost = (-0.5)*edge.reverse_cost;
        } else {
            graph[e].cost = edge.reverse_cost;
        }
 
        graph[e].id = normal? edge.id : -edge.id;
      }
}

Referenced by pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::insert_negative_edges().

has_vertex()

template<typename G , typename T_V , typename T_E >

bool pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::has_vertex ( int64_t  vid ) const

inlineinherited

True when vid is in the graph.

Definition at line 534 of file pgr_base_graph.hpp.

                                        {
         return vertices_map.find(vid) != vertices_map.end();
     }

Referenced by pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::add_vertices(), pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::get_V(), pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::graph_add_edge_no_create_vertex(), pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::in_degree(), pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::insert_edges(), pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::out_degree(), and pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::Pgr_base_graph().

in_degree() [1/2]

template<typename G , typename T_V , typename T_E >

degree_size_type pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::in_degree ( int64_t  vertex_id ) const

inlineinherited

Definition at line 497 of file pgr_base_graph.hpp.

                                                         {
         if (!has_vertex(vertex_id)) {
             return 0;
         }
         return is_directed()?
             in_degree(get_V(vertex_id))
             :  out_degree(get_V(vertex_id));
     }

Referenced by pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::in_degree().

in_degree() [2/2]

template<typename G , typename T_V , typename T_E >

degree_size_type pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::in_degree ( V &  v ) const

inlineinherited

in degree of a vertex

• when its undirected there is no "concept" of in degree
  • out degree is returned
• on directed in degree of vertex is returned

Definition at line 576 of file pgr_base_graph.hpp.

                                            {
         return is_directed()?
             boost::in_degree(v, graph) :
             boost::out_degree(v, graph);
     }

insert_edges() [1/3]

template<typename G , typename T_V , typename T_E >

template<typename T >

void pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::insert_edges ( const std::vector< T > &  edges, bool  normal = true  )

inlineinherited

Inserts count edges of type pgr_edge_t into the graph The set of edges should not have an illegal vertex defined When the graph is empty calls:

• extract_vertices and throws an exception if there are illegal vertices. When developing:
  • if an illegal vertex is found an exception is thrown
  • That means that the set of vertices should be checked in the code that is being developed No edge is inserted when there is an error on the vertices

    Parameters

    edges
    normal

Definition at line 395 of file pgr_base_graph.hpp.

                                                                 {
#if 0
         // This code does not work with contraction
         if (num_vertices() == 0) {
             auto vertices = pgrouting::extract_vertices(edges);
             pgassert(pgrouting::check_vertices(vertices) == 0);
             add_vertices(vertices);
         }
#endif
         for (const auto edge : edges) {
             graph_add_edge(edge, normal);
         }
     }

insert_edges() [2/3]

template<typename G , typename T_V , typename T_E >

template<typename T >

void pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::insert_edges ( const T *  edges, size_t  count  )

inlineinherited

Inserts count edges of type T into the graph.

Converts the edges to a std::vector<T> & calls the overloaded twin function.

Parameters

edges
count

Definition at line 357 of file pgr_base_graph.hpp.

                                                         {
             insert_edges(std::vector < T >(edges, edges + count));
         }

Referenced by do_pgr_articulationPoints(), do_pgr_astarManyToMany(), do_pgr_bdAstar(), do_pgr_bdDijkstra(), do_pgr_bellman_ford(), do_pgr_bellman_ford_neg(), do_pgr_biconnectedComponents(), do_pgr_binaryBreadthFirstSearch(), do_pgr_bipartite(), do_pgr_boyerMyrvold(), do_pgr_breadthFirstSearch(), do_pgr_bridges(), do_pgr_combinations_dijkstra(), do_pgr_connectedComponents(), do_pgr_dagShortestPath(), do_pgr_depthFirstSearch(), do_pgr_dijkstraVia(), do_pgr_driving_many_to_dist(), do_pgr_edwardMoore(), do_pgr_floydWarshall(), do_pgr_isPlanar(), do_pgr_johnson(), do_pgr_kruskal(), do_pgr_ksp(), do_pgr_LTDTree(), do_pgr_makeConnected(), do_pgr_many_to_many_dijkstra(), do_pgr_many_withPointsDD(), do_pgr_randomSpanningTree(), do_pgr_sequentialVertexColoring(), do_pgr_stoerWagner(), do_pgr_strongComponents(), do_pgr_topologicalSort(), do_pgr_transitiveClosure(), do_pgr_turnRestrictedPath(), do_pgr_withPoints(), do_pgr_withPointsKsp(), pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::insert_edges(), pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::insert_edges_neg(), pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::insert_min_edges_no_parallel(), and pgrouting::alphashape::Pgr_alphaShape::Pgr_alphaShape().

insert_edges() [3/3]

template<typename G , typename T_V , typename T_E >

template<typename T >

void pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::insert_edges ( T *  edges, size_t  count, bool    )

inlineinherited

Definition at line 367 of file pgr_base_graph.hpp.

                                                         {
             for (size_t i = 0; i < count; ++i) {
                 pgassert(has_vertex(edges[i].source));
                 pgassert(has_vertex(edges[i].target));
                 graph_add_edge_no_create_vertex(edges[i]);
             }
         }

insert_edges_neg()

template<typename G , typename T_V , typename T_E >

template<typename T >

void pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::insert_edges_neg ( const T *  edges, size_t  count  )

inlineinherited

Definition at line 362 of file pgr_base_graph.hpp.

                                                             {
             insert_edges(std::vector < T >(edges, edges + count), false);
         }

Referenced by do_pgr_lineGraph(), and do_pgr_lineGraphFull().

insert_min_edges_no_parallel() [1/2]

template<typename G , typename T_V , typename T_E >

template<typename T >

void pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::insert_min_edges_no_parallel ( const std::vector< T > &  edges )

inlineinherited

Definition at line 416 of file pgr_base_graph.hpp.

                                                             {
         for (const auto edge : edges) {
             graph_add_min_edge_no_parallel(edge);
         }
     }

insert_min_edges_no_parallel() [2/2]

template<typename G , typename T_V , typename T_E >

template<typename T >

void pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::insert_min_edges_no_parallel ( const T *  edges, size_t  count  )

inlineinherited

Definition at line 410 of file pgr_base_graph.hpp.

                                                                     {
         insert_edges(std::vector<T>(edges, edges + count));
     }

Referenced by do_pgr_prim().

insert_negative_edges() [1/2]

template<typename G , typename T_V , typename T_E >

template<typename T >

void pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::insert_negative_edges ( const std::vector< T > &  edges, bool  normal = true  )

inlineinherited

Definition at line 423 of file pgr_base_graph.hpp.

                                 {
         for (const auto edge : edges) {
             graph_add_neg_edge(edge, normal);
         }
     }

insert_negative_edges() [2/2]

template<typename G , typename T_V , typename T_E >

template<typename T >

void pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::insert_negative_edges ( const T *  edges, int64_t  count  )

inlineinherited

Definition at line 376 of file pgr_base_graph.hpp.

                                                                   {
             insert_negative_edges(std::vector < T >(edges, edges + count));
         }

Referenced by do_pgr_bellman_ford_neg(), and pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::insert_negative_edges().

insert_vertices()

template<class G , typename T_V , typename T_E >

void pgrouting::graph::Pgr_lineGraph< G, T_V, T_E >::insert_vertices ( const pgrouting::DirectedGraph &  digraph )

inline

Definition at line 134 of file pgr_lineGraph.hpp.

                                                   {
        auto es = boost::edges(digraph.graph);
        for (auto eit = es.first; eit != es.second; ++eit) {
            auto edge = *eit;
            Line_vertex vertex({
                    digraph[edge].id,
                    digraph[boost::source(edge, digraph.graph)].id,
                    digraph[boost::target(edge, digraph.graph)].id,
                    digraph[edge].cost,
                    -1});
            add_one_vertex(vertex);
        }
    }

References pgrouting::graph::Pgr_lineGraph< G, T_V, T_E >::add_one_vertex(), and pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::graph.

Referenced by pgrouting::graph::Pgr_lineGraph< G, T_V, T_E >::Pgr_lineGraph().

is_directed()

template<typename G , typename T_V , typename T_E >

bool pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::is_directed ( ) const

inlineinherited

Definition at line 543 of file pgr_base_graph.hpp.

{return m_gType == DIRECTED;}

Referenced by pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::graph_add_edge_no_create_vertex(), and pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::in_degree().

is_source()

template<typename G , typename T_V , typename T_E >

bool pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::is_source ( V  v_idx, E  e_idx  ) const

inlineinherited

Definition at line 545 of file pgr_base_graph.hpp.

{return v_idx == source(e_idx);}

Referenced by pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::adjacent().

is_target()

template<typename G , typename T_V , typename T_E >

bool pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::is_target ( V  v_idx, E  e_idx  ) const

inlineinherited

Definition at line 546 of file pgr_base_graph.hpp.

{return v_idx == target(e_idx);}

Referenced by pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::adjacent().

is_undirected()

template<typename G , typename T_V , typename T_E >

bool pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::is_undirected ( ) const

inlineinherited

Definition at line 544 of file pgr_base_graph.hpp.

{return m_gType == UNDIRECTED;}

Referenced by pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::graph_add_edge_no_create_vertex().

num_edges()

template<typename G , typename T_V , typename T_E >

size_t pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::num_edges ( ) const

inlineinherited

Definition at line 704 of file pgr_base_graph.hpp.

{ return boost::num_edges(graph);}

Referenced by pgrouting::graph::Pgr_lineGraph< G, T_V, T_E >::graph_add_edge().

num_vertices()

template<typename G , typename T_V , typename T_E >

size_t pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::num_vertices ( ) const

inlineinherited

Definition at line 703 of file pgr_base_graph.hpp.

{ return boost::num_vertices(graph);}

Referenced by pgrouting::graph::Pgr_lineGraph< G, T_V, T_E >::add_one_vertex(), pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::add_vertices(), pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::get_V(), pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::insert_edges(), and pgrouting::graph::Pgr_lineGraphFull< G, T_V, T_E >::insert_vertex().

operator[]() [1/4]

template<typename G , typename T_V , typename T_E >

T_E& pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::operator[] ( E  e_idx )

inlineinherited

Definition at line 554 of file pgr_base_graph.hpp.

{return graph[e_idx];}

operator[]() [2/4]

template<typename G , typename T_V , typename T_E >

const T_E& pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::operator[] ( E  e_idx ) const

inlineinherited

Definition at line 555 of file pgr_base_graph.hpp.

{return graph[e_idx];}

operator[]() [3/4]

template<typename G , typename T_V , typename T_E >

T_V& pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::operator[] ( V  v_idx )

inlineinherited

Definition at line 557 of file pgr_base_graph.hpp.

{return graph[v_idx];}

operator[]() [4/4]

template<typename G , typename T_V , typename T_E >

const T_V& pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::operator[] ( V  v_idx ) const

inlineinherited

Definition at line 558 of file pgr_base_graph.hpp.

{return graph[v_idx];}

out_degree() [1/2]

template<typename G , typename T_V , typename T_E >

degree_size_type pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::out_degree ( int64_t  vertex_id ) const

inlineinherited

get the out-degree of a vertex

Returns

0: The out degree of a vertex that its not in the graph

Parameters

[in]

vertex_id

original vertex id

Definition at line 489 of file pgr_base_graph.hpp.

                                                          {
         if (!has_vertex(vertex_id)) {
             return 0;
         }
         auto v = get_V(vertex_id);
         auto d = out_degree(v);
         return d;
     }

Referenced by pgrouting::algorithms::bridges(), pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::in_degree(), and pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::out_degree().

out_degree() [2/2]

template<typename G , typename T_V , typename T_E >

degree_size_type pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::out_degree ( V &  v ) const

inlineinherited

out degree of a vertex

regardles of undirected or directed graph

• out degree is returned

Definition at line 587 of file pgr_base_graph.hpp.

                                             {
         return boost::out_degree(v, graph);
     }

restore_graph()

template<class G , typename T_V , typename T_E >

void pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::restore_graph

inherited

Reconnects all edges that were removed.

Definition at line 866 of file pgr_base_graph.hpp.

                                             {
    while (removed_edges.size() != 0) {
        graph_add_edge(removed_edges[0]);
        removed_edges.pop_front();
    }
}

source()

template<typename G , typename T_V , typename T_E >

V pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::source ( E  e_idx ) const

inlineinherited

Definition at line 560 of file pgr_base_graph.hpp.

{return boost::source(e_idx, graph);}

Referenced by pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::adjacent(), pgrouting::graph::Pgr_lineGraphFull< G, T_V, T_E >::apply_transformation(), pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::get_edge(), pgrouting::graph::Pgr_lineGraphFull< G, T_V, T_E >::get_postgres_results_directed(), pgrouting::graph::Pgr_lineGraph< G, T_V, T_E >::get_postgres_results_directed(), pgrouting::graph::Pgr_lineGraphFull< G, T_V, T_E >::graph_add_edge(), pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::insert_edges(), pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::is_source(), pgrouting::alphashape::Pgr_alphaShape::make_triangles(), and pgrouting::alphashape::Pgr_alphaShape::radius().

target()

template<typename G , typename T_V , typename T_E >

V pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::target ( E  e_idx ) const

inlineinherited

Definition at line 561 of file pgr_base_graph.hpp.

{return boost::target(e_idx, graph);}

Referenced by pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::adjacent(), pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::get_edge(), pgrouting::graph::Pgr_lineGraphFull< G, T_V, T_E >::get_postgres_results_directed(), pgrouting::graph::Pgr_lineGraph< G, T_V, T_E >::get_postgres_results_directed(), pgrouting::graph::Pgr_lineGraphFull< G, T_V, T_E >::graph_add_edge(), pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::insert_edges(), pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::is_target(), pgrouting::alphashape::Pgr_alphaShape::make_triangles(), and pgrouting::alphashape::Pgr_alphaShape::radius().

Friends And Related Function Documentation

operator<<

template<class G , typename T_V , typename T_E >

std::ostream& operator<< ( std::ostream &  log, const Pgr_lineGraph< G, T_V, T_E > &  g  )

friend

Definition at line 69 of file pgr_lineGraph.hpp.

                                                                    {
        typename Pgr_base_graph< G, T_V, T_E >::EO_i out, out_end;
 
        for (auto vi = vertices(g.graph).first;
                vi != vertices(g.graph).second; ++vi) {
            if ((*vi) >= g.num_vertices()) break;
            log << (*vi) << ": " << " out_edges_of(" << g.graph[(*vi)] << "):";
            for (boost::tie(out, out_end) = out_edges(*vi, g.graph);
                    out != out_end; ++out) {
                log << ' '
                    << g.graph[*out].id << "=("
                    << g[g.source(*out)].id << ", "
                    << g[g.target(*out)].id << ")\t";
            }
            log << std::endl;
        }
        return log;
    }

Member Data Documentation

graph

template<typename G , typename T_V , typename T_E >

G pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::graph

inherited

The graph.

Definition at line 260 of file pgr_base_graph.hpp.

Referenced by pgrouting::graph::Pgr_lineGraph< G, T_V, T_E >::add_one_vertex(), pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::add_vertices(), pgrouting::graph::Pgr_lineGraphFull< G, T_V, T_E >::apply_transformation(), pgrouting::algorithms::articulationPoints(), pgrouting::algorithms::biconnectedComponents(), pgrouting::algorithms::bridges(), pgrouting::graph::Pgr_lineGraph< G, T_V, T_E >::create_edges(), pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::get_edge(), pgrouting::graph::Pgr_lineGraphFull< G, T_V, T_E >::get_postgres_results_directed(), pgrouting::graph::Pgr_lineGraph< G, T_V, T_E >::get_postgres_results_directed(), pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::get_V(), pgrouting::graph::Pgr_lineGraph< G, T_V, T_E >::graph_add_edge(), pgrouting::graph::Pgr_lineGraphFull< G, T_V, T_E >::graph_add_edge(), pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::graph_add_edge_no_create_vertex(), pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::in_degree(), pgrouting::graph::Pgr_lineGraphFull< G, T_V, T_E >::insert_vertex(), pgrouting::graph::Pgr_lineGraph< G, T_V, T_E >::insert_vertices(), pgrouting::alphashape::Pgr_alphaShape::make_triangles(), pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::num_edges(), pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::num_vertices(), pgrouting::alphashape::Pgr_alphaShape::operator()(), pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::operator[](), pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::out_degree(), pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::Pgr_base_graph(), pgrouting::algorithms::pgr_connectedComponents(), pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::source(), pgrouting::graph::Pgr_lineGraphFull< G, T_V, T_E >::store_edge_costs(), pgrouting::algorithms::strongComponents(), and pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::target().

log

template<class G , typename T_V , typename T_E >

std::ostringstream pgrouting::graph::Pgr_lineGraph< G, T_V, T_E >::log

Definition at line 216 of file pgr_lineGraph.hpp.

m_edges

template<class G , typename T_V , typename T_E >

std::map< int64_t, pgr_edge_t > pgrouting::graph::Pgr_lineGraph< G, T_V, T_E >::m_edges

private

Definition at line 213 of file pgr_lineGraph.hpp.

m_gType

template<typename G , typename T_V , typename T_E >

graphType pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::m_gType

inherited

type (DIRECTED or UNDIRECTED)

Definition at line 261 of file pgr_base_graph.hpp.

Referenced by pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::is_directed(), and pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::is_undirected().

mapIndex

template<typename G , typename T_V , typename T_E >

IndexMap pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::mapIndex

inherited

Definition at line 272 of file pgr_base_graph.hpp.

propmapIndex

template<typename G , typename T_V , typename T_E >

boost::associative_property_map<IndexMap> pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::propmapIndex

inherited

Definition at line 273 of file pgr_base_graph.hpp.

Referenced by pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::get_V().

removed_edges

template<typename G , typename T_V , typename T_E >

std::deque< T_E > pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::removed_edges

inherited

Used for storing the removed_edges.

Definition at line 281 of file pgr_base_graph.hpp.

vertices_map

template<typename G , typename T_V , typename T_E >

id_to_V pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::vertices_map

inherited

id -> graph id

Definition at line 267 of file pgr_base_graph.hpp.

Referenced by pgrouting::graph::Pgr_lineGraph< G, T_V, T_E >::add_one_vertex(), pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::add_vertices(), pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::get_V(), pgrouting::graph::Pgr_lineGraphFull< G, T_V, T_E >::graph_add_edge(), pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::graph_add_edge_no_create_vertex(), pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::has_vertex(), pgrouting::graph::Pgr_lineGraphFull< G, T_V, T_E >::insert_vertex(), and pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::Pgr_base_graph().

vertIndex

template<typename G , typename T_V , typename T_E >

boost::property_map<G, boost::vertex_index_t>::type pgrouting::graph::Pgr_base_graph< G, T_V, T_E >::vertIndex

inherited

Definition at line 269 of file pgr_base_graph.hpp.

Referenced by pgrouting::graph::Pgr_base_graph< BG, XY_vertex, Basic_edge >::Pgr_base_graph().

---

The documentation for this class was generated from the following file:

• pgr_lineGraph.hpp