pgr_depthFirstSearch - Proposed

pgr_depthFirstSearch — Returns a depth first search traversal of the graph. The graph can be directed or undirected.

Boost Graph Inside

Warning

Proposed functions for next mayor release.

• They are not officially in the current release.

• They will likely officially be part of the next mayor release:

  • The functions make use of ANY-INTEGER and ANY-NUMERICAL

  • Name might not change. (But still can)

  • Signature might not change. (But still can)

  • Functionality might not change. (But still can)

  • pgTap tests have being done. But might need more.

  • Documentation might need refinement.

Availability

• Version 3.3.0

  • Promoted to proposed function

• Version 3.2.0

  • New experimental signatures:

    • pgr_depthFirstSearch (Single Vertex)

    • pgr_depthFirstSearch (Multiple Vertices)

Description

Depth First Search algorithm is a traversal algorithm which starts from a root vertex, goes as deep as possible, and backtracks once a vertex is reached with no adjacent vertices or with all visited adjacent vertices. The traversal continues until all the vertices reachable from the root vertex are visited.

The main Characteristics are:

• The implementation works for both directed and undirected graphs.

• Provides the Depth First Search traversal order from a root vertex or from a set of root vertices.

• An optional non-negative maximum depth parameter to limit the results up to a particular depth.

• For optimization purposes, any duplicated values in the Root vids are ignored.

• It does not produce the shortest path from a root vertex to a target vertex.

• The aggregate cost of traversal is not guaranteed to be minimal.

• The returned values are ordered in ascending order of start_vid.

• Depth First Search Running time: \(O(E + V)\)

Signatures

Summary

pgr_depthFirstSearch(Edges SQL, root vid, [options])

pgr_depthFirstSearch(Edges SQL, root vids, [options])

options: [directed, max_depth]

Returns set of (seq, depth, start_vid, node, edge, cost, agg_cost)

Single vertex

pgr_depthFirstSearch(Edges SQL, root vid, [options])

options: [directed, max_depth]

Returns set of (seq, depth, start_vid, node, edge, cost, agg_cost)

Example:

From root vertex \(6\) on a directed graph with edges in ascending order of id

SELECT * FROM pgr_depthFirstSearch(
  'SELECT id, source, target, cost, reverse_cost FROM edges
  ORDER BY id',
  6);
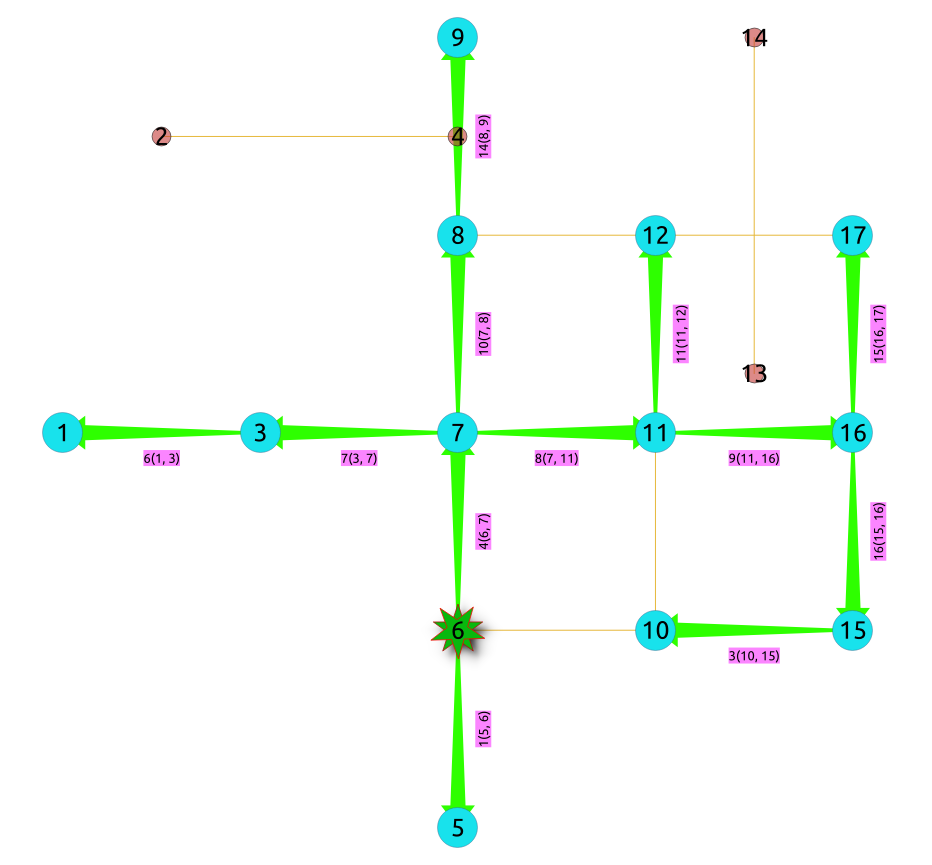
 seq | depth | start_vid | node | edge | cost | agg_cost
-----+-------+-----------+------+------+------+----------
   1 |     0 |         6 |    6 |   -1 |    0 |        0
   2 |     1 |         6 |    5 |    1 |    1 |        1
   3 |     1 |         6 |    7 |    4 |    1 |        1
   4 |     2 |         6 |    3 |    7 |    1 |        2
   5 |     3 |         6 |    1 |    6 |    1 |        3
   6 |     2 |         6 |   11 |    8 |    1 |        2
   7 |     3 |         6 |   16 |    9 |    1 |        3
   8 |     4 |         6 |   17 |   15 |    1 |        4
   9 |     4 |         6 |   15 |   16 |    1 |        4
  10 |     5 |         6 |   10 |    3 |    1 |        5
  11 |     3 |         6 |   12 |   11 |    1 |        3
  12 |     2 |         6 |    8 |   10 |    1 |        2
  13 |     3 |         6 |    9 |   14 |    1 |        3
(13 rows)

Multiple vertices

pgr_depthFirstSearch(Edges SQL, root vids, [options])

options: [directed, max_depth]

Returns set of (seq, depth, start_vid, node, edge, cost, agg_cost)

Example:

From root vertices \(\{12, 6\}\) on an undirected graph with depth \(<= 2\) and edges in ascending order of id

SELECT * FROM pgr_depthFirstSearch(
  'SELECT id, source, target, cost, reverse_cost FROM edges
  ORDER BY id',
  ARRAY[12, 6], directed => false, max_depth => 2);
 seq | depth | start_vid | node | edge | cost | agg_cost
-----+-------+-----------+------+------+------+----------
   1 |     0 |         6 |    6 |   -1 |    0 |        0
   2 |     1 |         6 |    5 |    1 |    1 |        1
   3 |     1 |         6 |   10 |    2 |    1 |        1
   4 |     2 |         6 |   15 |    3 |    1 |        2
   5 |     2 |         6 |   11 |    5 |    1 |        2
   6 |     1 |         6 |    7 |    4 |    1 |        1
   7 |     2 |         6 |    3 |    7 |    1 |        2
   8 |     2 |         6 |    8 |   10 |    1 |        2
   9 |     0 |        12 |   12 |   -1 |    0 |        0
  10 |     1 |        12 |   11 |   11 |    1 |        1
  11 |     2 |        12 |   10 |    5 |    1 |        2
  12 |     2 |        12 |    7 |    8 |    1 |        2
  13 |     2 |        12 |   16 |    9 |    1 |        2
  14 |     1 |        12 |    8 |   12 |    1 |        1
  15 |     2 |        12 |    9 |   14 |    1 |        2
  16 |     1 |        12 |   17 |   13 |    1 |        1
(16 rows)

Parameters

Parameter	Type	Description
Edges SQL	TEXT	Edges SQL as described below.
root vid	BIGINT	Identifier of the root vertex of the tree. When value is \(0\) then gets the spanning forest starting in aleatory nodes for each tree in the forest.
root vids	ARRAY [ ANY-INTEGER ]	Array of identifiers of the root vertices. \(0\) values are ignored For optimization purposes, any duplicated value is ignored.

Where:

ANY-INTEGER:

SMALLINT, INTEGER, BIGINT

ANY-NUMERIC:

SMALLINT, INTEGER, BIGINT, REAL, FLOAT, NUMERIC

Optional parameters

Column	Type	Default	Description
directed	BOOLEAN	true	When true the graph is considered Directed When false the graph is considered as Undirected.

DFS optional parameters

Parameter	Type	Default	Description
max_depth	BIGINT	\(9223372036854775807\)	Upper limit of the depth of the tree. When negative throws an error.

Inner Queries

Edges SQL

Column	Type	Default	Description
id	ANY-INTEGER		Identifier of the edge.
source	ANY-INTEGER		Identifier of the first end point vertex of the edge.
target	ANY-INTEGER		Identifier of the second end point vertex of the edge.
cost	ANY-NUMERICAL		Weight of the edge (source, target)
reverse_cost	ANY-NUMERICAL	-1	Weight of the edge (target, source) When negative: edge (target, source) does not exist, therefore it’s not part of the graph.

Where:

ANY-INTEGER:

SMALLINT, INTEGER, BIGINT

ANY-NUMERICAL:

SMALLINT, INTEGER, BIGINT, REAL, FLOAT

Result columns

Returns set of (seq, depth, start_vid, node, edge, cost, agg_cost)

Parameter	Type	Description
seq	BIGINT	Sequential value starting from \(1\).
depth	BIGINT	Depth of the node. \(0\) when node = start_vid.
start_vid	BIGINT	Identifier of the root vertex.
node	BIGINT	Identifier of node reached using edge.
edge	BIGINT	Identifier of the edge used to arrive to node. \(-1\) when node = start_vid.
cost	FLOAT	Cost to traverse edge.
agg_cost	FLOAT	Aggregate cost from start_vid to node.

Where:

ANY-INTEGER:

SMALLINT, INTEGER, BIGINT

ANY-NUMERIC:

SMALLINT, INTEGER, BIGINT, REAL, FLOAT, NUMERIC

Additional Examples

Example:

Same as Single vertex but with edges in descending order of id.

SELECT * FROM pgr_depthFirstSearch(
  'SELECT id, source, target, cost, reverse_cost FROM edges
  ORDER BY id DESC',
  6);
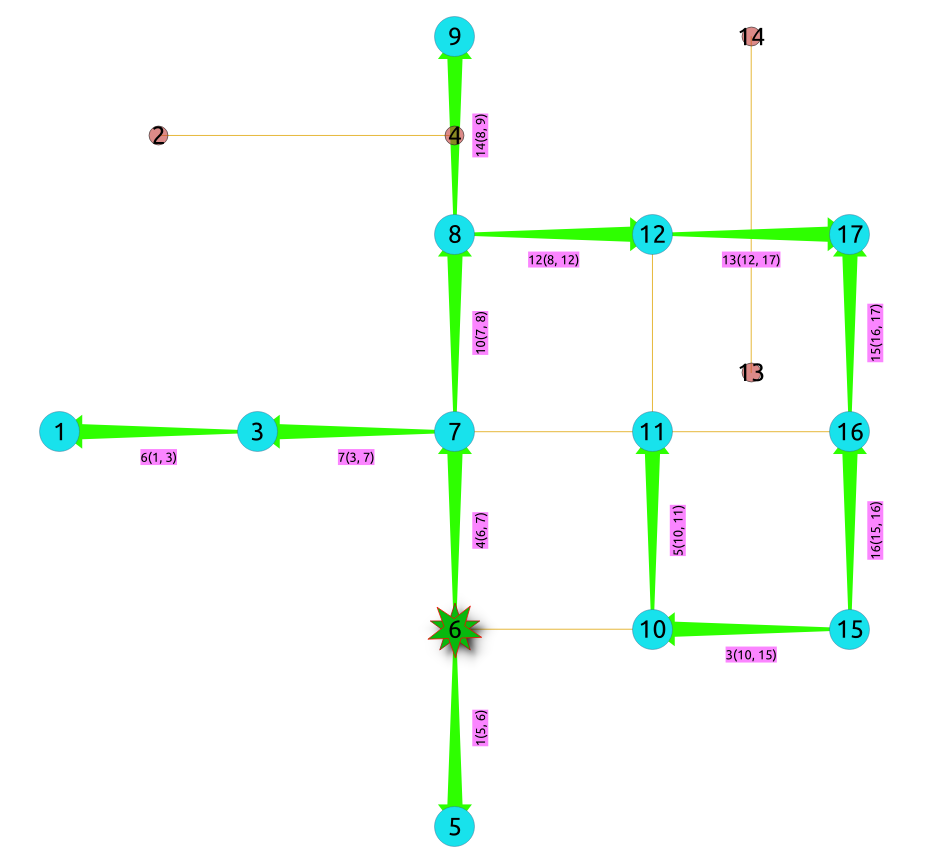
 seq | depth | start_vid | node | edge | cost | agg_cost
-----+-------+-----------+------+------+------+----------
   1 |     0 |         6 |    6 |   -1 |    0 |        0
   2 |     1 |         6 |    7 |    4 |    1 |        1
   3 |     2 |         6 |    8 |   10 |    1 |        2
   4 |     3 |         6 |    9 |   14 |    1 |        3
   5 |     3 |         6 |   12 |   12 |    1 |        3
   6 |     4 |         6 |   17 |   13 |    1 |        4
   7 |     5 |         6 |   16 |   15 |    1 |        5
   8 |     6 |         6 |   15 |   16 |    1 |        6
   9 |     7 |         6 |   10 |    3 |    1 |        7
  10 |     8 |         6 |   11 |    5 |    1 |        8
  11 |     2 |         6 |    3 |    7 |    1 |        2
  12 |     3 |         6 |    1 |    6 |    1 |        3
  13 |     1 |         6 |    5 |    1 |    1 |        1
(13 rows)

The resulting traversal is different.

The left image shows the result with ascending order of ids and the right image shows with descending order of the edge identifiers.

See Also

• DFS - Category

• Sample Data

• Boost: Depth First Search algorithm documentation

• Boost: Undirected DFS algorithm documentation

• Wikipedia: Depth First Search algorithm

Indices and tables

• Index

• Search Page