pgr_dijkstra¶
pgr_dijkstra — Ruta(s) más corta(s) usando el algoritmo Dijkstra.
Adentro: Boost Graph¶
Disponibilidad
Versión 3.5.0
Standarizing output columns to
(seq, path_seq, start_vid, end_vid, node, edge, cost, agg_cost)pgr_dijkstra(Uno a Uno) ha añadido las columnas start_vid y end_vid.pgr_dijkstra(Uno a Muchos) ha añadido la columnaend_vid.pgr_dijkstra(Muchos a Uno) ha añadido la columna start_vid.
Versión 3.1.0
Nuevas funciones Propuestas:
pgr_dijkstra(Combinaciones)
Versión 3.0.0
Funciones oficiales
Version 2.2.0
Nuevas funciones propuestas:
pgr_dijkstra(Uno a Muchos)pgr_dijkstra(Muchos a Uno)pgr_dijkstra(Muchos a Muchos)
Versión 2.1.0
Cambio de firma en
pgr_dijkstra(Uno a Uno)
Versión 2.0.0
Oficial
pgr_dijkstra(Uno a Uno)
Descripción¶
Algoritmo de Dijkstra, concebido por el informático holandés Edsger Dijkstra en 1956. Es un algoritmo de búsqueda en grafos que resuelve el problema de ruta más corta para un grafo con costos de aristas no negativos, produciendo la ruta más corta desde un vértice inicial a un vértice final . Esta implementación se puede utilizar con un grafos dirigidos y no dirigidos.
El proceso se realiza sólo en aristas con costos positivos.
Valor no negativo en una columna de costo se interpreta como la arista no exite.
Los valores se devuelven cuando hay una ruta.
Cuando no hay ruta:
Cuando el vértice de salida y el vértice destino son iguales.
El costo agregado de los valores no incluídos \((v, v)\) es \(0\)
Cuando el vértice de salida y el vértice destino son diferentes y no hay ninguna ruta:
El costo agregado de los valores no incluídos \((u, v)\) es :math: infty
Para fines de optimización, se ignora cualquier valor duplicado en los vertices de salida o destino.
Tiempo de ejecución: \(O(| start\_vids | * (V \log V + E))\)
Firmas¶
Resumen
pgr_dijkstra(Edges SQL, start vid, end vid, [
directed])pgr_dijkstra(Edges SQL, start vid, end vids, [
directed])pgr_dijkstra(Edges SQL, start vids, end vid, [
directed])pgr_dijkstra(Edges SQL, start vids, end vids, [
directed])RETURNS SET OF
(seq, path_seq, start_vid, end_vid, node, edge, cost, agg_cost)OR EMPTY SET
Advertencia
Cambio de ruptura en 3.5.0
Leer Guía de migración sobre como migrar de las columnas de resultados anteriores a las nuevas columnas de resultados.
Uno a Uno¶
pgr_dijkstra(Edges SQL, start vid, end vid, [
directed])RETURNS SET OF
(seq, path_seq, start_vid, end_vid, node, edge, cost, agg_cost)OR EMPTY SET
- Ejemplo:
Del vértice \(6\) al vértice \(10\) en un grafo dirigido
SELECT * FROM pgr_Dijkstra(
'select id, source, target, cost, reverse_cost from edges',
6, 10, true);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 10 | 6 | 4 | 1 | 0
2 | 2 | 6 | 10 | 7 | 8 | 1 | 1
3 | 3 | 6 | 10 | 11 | 9 | 1 | 2
4 | 4 | 6 | 10 | 16 | 16 | 1 | 3
5 | 5 | 6 | 10 | 15 | 3 | 1 | 4
6 | 6 | 6 | 10 | 10 | -1 | 0 | 5
(6 rows)
Uno a Muchos¶
pgr_dijkstra(Edges SQL, start vid, end vids, [
directed])RETURNS SET OF
(seq, path_seq, start_vid, end_vid, node, edge, cost, agg_cost)OR EMPTY SET
- Ejemplo:
Del vértice \(6\) a los vértices \(\{10, 17\}\) en un grafo no dirigido
SELECT * FROM pgr_Dijkstra(
'select id, source, target, cost, reverse_cost from edges',
6, ARRAY[10, 17]);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 10 | 6 | 4 | 1 | 0
2 | 2 | 6 | 10 | 7 | 8 | 1 | 1
3 | 3 | 6 | 10 | 11 | 9 | 1 | 2
4 | 4 | 6 | 10 | 16 | 16 | 1 | 3
5 | 5 | 6 | 10 | 15 | 3 | 1 | 4
6 | 6 | 6 | 10 | 10 | -1 | 0 | 5
7 | 1 | 6 | 17 | 6 | 4 | 1 | 0
8 | 2 | 6 | 17 | 7 | 8 | 1 | 1
9 | 3 | 6 | 17 | 11 | 9 | 1 | 2
10 | 4 | 6 | 17 | 16 | 15 | 1 | 3
11 | 5 | 6 | 17 | 17 | -1 | 0 | 4
(11 rows)
Muchos a Uno¶
pgr_dijkstra(Edges SQL, start vids, end vid, [
directed])RETURNS SET OF
(seq, path_seq, start_vid, end_vid, node, edge, cost, agg_cost)OR EMPTY SET
- Ejemplo:
De los vértices \(\{6, 1\}\) al vertice \(17\) en un grafo dirigido
SELECT * FROM pgr_Dijkstra(
'select id, source, target, cost, reverse_cost from edges',
ARRAY[6, 1], 17);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 1 | 17 | 1 | 6 | 1 | 0
2 | 2 | 1 | 17 | 3 | 7 | 1 | 1
3 | 3 | 1 | 17 | 7 | 8 | 1 | 2
4 | 4 | 1 | 17 | 11 | 11 | 1 | 3
5 | 5 | 1 | 17 | 12 | 13 | 1 | 4
6 | 6 | 1 | 17 | 17 | -1 | 0 | 5
7 | 1 | 6 | 17 | 6 | 4 | 1 | 0
8 | 2 | 6 | 17 | 7 | 8 | 1 | 1
9 | 3 | 6 | 17 | 11 | 11 | 1 | 2
10 | 4 | 6 | 17 | 12 | 13 | 1 | 3
11 | 5 | 6 | 17 | 17 | -1 | 0 | 4
(11 rows)
Muchos a Muchos¶
pgr_dijkstra(Edges SQL, start vids, end vids, [
directed])RETURNS SET OF
(seq, path_seq, start_vid, end_vid, node, edge, cost, agg_cost)OR EMPTY SET
- Ejemplo:
De los vértices \(\{6, 1\}\) a los vértices \(\{10, 17\}\) en un grafo no dirigido
SELECT * FROM pgr_Dijkstra(
'select id, source, target, cost, reverse_cost from edges',
ARRAY[6, 1], ARRAY[10, 17],
directed => false);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 1 | 10 | 1 | 6 | 1 | 0
2 | 2 | 1 | 10 | 3 | 7 | 1 | 1
3 | 3 | 1 | 10 | 7 | 4 | 1 | 2
4 | 4 | 1 | 10 | 6 | 2 | 1 | 3
5 | 5 | 1 | 10 | 10 | -1 | 0 | 4
6 | 1 | 1 | 17 | 1 | 6 | 1 | 0
7 | 2 | 1 | 17 | 3 | 7 | 1 | 1
8 | 3 | 1 | 17 | 7 | 8 | 1 | 2
9 | 4 | 1 | 17 | 11 | 9 | 1 | 3
10 | 5 | 1 | 17 | 16 | 15 | 1 | 4
11 | 6 | 1 | 17 | 17 | -1 | 0 | 5
12 | 1 | 6 | 10 | 6 | 2 | 1 | 0
13 | 2 | 6 | 10 | 10 | -1 | 0 | 1
14 | 1 | 6 | 17 | 6 | 4 | 1 | 0
15 | 2 | 6 | 17 | 7 | 8 | 1 | 1
16 | 3 | 6 | 17 | 11 | 11 | 1 | 2
17 | 4 | 6 | 17 | 12 | 13 | 1 | 3
18 | 5 | 6 | 17 | 17 | -1 | 0 | 4
(18 rows)
Combinaciones¶
RETURNS SET OF
(seq, path_seq, start_vid, end_vid, node, edge, cost, agg_cost)OR EMPTY SET
- Ejemplo:
Usando una tabla de combinaciones en un grafo no dirigido
La tabla de combinaciones:
SELECT source, target FROM combinations;
source | target
--------+--------
5 | 6
5 | 10
6 | 5
6 | 15
6 | 14
(5 rows)
La consulta:
SELECT * FROM pgr_Dijkstra(
'SELECT id, source, target, cost, reverse_cost FROM edges',
'SELECT source, target FROM combinations',
false);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 5 | 6 | 5 | 1 | 1 | 0
2 | 2 | 5 | 6 | 6 | -1 | 0 | 1
3 | 1 | 5 | 10 | 5 | 1 | 1 | 0
4 | 2 | 5 | 10 | 6 | 2 | 1 | 1
5 | 3 | 5 | 10 | 10 | -1 | 0 | 2
6 | 1 | 6 | 5 | 6 | 1 | 1 | 0
7 | 2 | 6 | 5 | 5 | -1 | 0 | 1
8 | 1 | 6 | 15 | 6 | 2 | 1 | 0
9 | 2 | 6 | 15 | 10 | 3 | 1 | 1
10 | 3 | 6 | 15 | 15 | -1 | 0 | 2
(10 rows)
Parámetros¶
Columna |
Tipo |
Descripción |
|---|---|---|
|
SQL de aristas como se describe a continuación |
|
|
SQL de combinaciones como se describe a abajo |
|
salida |
|
Identificador del vértice inicial de la ruta. |
salidas |
|
Arreglo de identificadores de vértices iniciales. |
destino |
|
Identificador del vértice final de la ruta. |
destinos |
|
Arreglo de identificadores de vértices finales. |
Parámetros opcionales¶
Columna |
Tipo |
x Defecto |
Descripción |
|---|---|---|---|
|
|
|
|
Consultas Internas¶
SQL aristas¶
Columna |
Tipo |
x Defecto |
Descripción |
|---|---|---|---|
|
ENTEROS |
Identificador de la arista. |
|
|
ENTEROS |
Identificador del primer vértice de la arista. |
|
|
ENTEROS |
Identificador del segundo vértice de la arista. |
|
|
FLOTANTES |
Peso de la arista ( |
|
|
FLOTANTES |
-1 |
Peso de la arista (
|
Donde:
- ENTEROS:
SMALLINT,INTEGER,BIGINT- FLOTANTES:
SMALLINT,INTEGER,BIGINT,REAL,FLOAT
SQL Combinaciones¶
Parámetro |
Tipo |
Descripción |
|---|---|---|
|
ENTEROS |
Identificador del vértice de salida. |
|
ENTEROS |
Identificador del vértice de llegada. |
Donde:
- ENTEROS:
SMALLINT,INTEGER,BIGINT
Columnas de Resultados¶
Devuelve el conjunto de (seq, path_seq [, start_vid] [, end_vid], node, edge, cost, agg_cost)
Columna |
Tipo |
Descripción |
|---|---|---|
|
|
Valor secuencial a partir de 1. |
|
|
Posición relativa en la ruta. Tiene el valor 1 para el inicio de una ruta. |
|
|
Identificador del vértice inicial. Se devuelve cuando hay varias vetrices iniciales en la consulta. |
|
|
Identificador del vértice final. Se devuelve cuando hay varios vértices finales en la consulta. |
|
|
Identificador del nodo en la ruta de |
|
|
Identificador de la arista utilizado para ir del |
|
|
Costo para atravesar desde |
|
|
Costo agregado desde |
Ejemplos Adicionales¶
- Ejemplo:
Demostración de ignorar los valores repertidos, y resultado ordenado.
SELECT * FROM pgr_Dijkstra(
'select id, source, target, cost, reverse_cost from edges',
ARRAY[7, 10, 15, 10, 10, 15], ARRAY[10, 7, 10, 15]);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 7 | 10 | 7 | 8 | 1 | 0
2 | 2 | 7 | 10 | 11 | 9 | 1 | 1
3 | 3 | 7 | 10 | 16 | 16 | 1 | 2
4 | 4 | 7 | 10 | 15 | 3 | 1 | 3
5 | 5 | 7 | 10 | 10 | -1 | 0 | 4
6 | 1 | 7 | 15 | 7 | 8 | 1 | 0
7 | 2 | 7 | 15 | 11 | 9 | 1 | 1
8 | 3 | 7 | 15 | 16 | 16 | 1 | 2
9 | 4 | 7 | 15 | 15 | -1 | 0 | 3
10 | 1 | 10 | 7 | 10 | 5 | 1 | 0
11 | 2 | 10 | 7 | 11 | 8 | 1 | 1
12 | 3 | 10 | 7 | 7 | -1 | 0 | 2
13 | 1 | 10 | 15 | 10 | 5 | 1 | 0
14 | 2 | 10 | 15 | 11 | 9 | 1 | 1
15 | 3 | 10 | 15 | 16 | 16 | 1 | 2
16 | 4 | 10 | 15 | 15 | -1 | 0 | 3
17 | 1 | 15 | 7 | 15 | 16 | 1 | 0
18 | 2 | 15 | 7 | 16 | 9 | 1 | 1
19 | 3 | 15 | 7 | 11 | 8 | 1 | 2
20 | 4 | 15 | 7 | 7 | -1 | 0 | 3
21 | 1 | 15 | 10 | 15 | 3 | 1 | 0
22 | 2 | 15 | 10 | 10 | -1 | 0 | 1
(22 rows)
- Ejemplo 2:
Haciendo vértices de salida igual que vértices destino
SELECT * FROM pgr_Dijkstra(
'select id, source, target, cost, reverse_cost from edges',
ARRAY[7, 10, 15], ARRAY[7, 10, 15]);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 7 | 10 | 7 | 8 | 1 | 0
2 | 2 | 7 | 10 | 11 | 9 | 1 | 1
3 | 3 | 7 | 10 | 16 | 16 | 1 | 2
4 | 4 | 7 | 10 | 15 | 3 | 1 | 3
5 | 5 | 7 | 10 | 10 | -1 | 0 | 4
6 | 1 | 7 | 15 | 7 | 8 | 1 | 0
7 | 2 | 7 | 15 | 11 | 9 | 1 | 1
8 | 3 | 7 | 15 | 16 | 16 | 1 | 2
9 | 4 | 7 | 15 | 15 | -1 | 0 | 3
10 | 1 | 10 | 7 | 10 | 5 | 1 | 0
11 | 2 | 10 | 7 | 11 | 8 | 1 | 1
12 | 3 | 10 | 7 | 7 | -1 | 0 | 2
13 | 1 | 10 | 15 | 10 | 5 | 1 | 0
14 | 2 | 10 | 15 | 11 | 9 | 1 | 1
15 | 3 | 10 | 15 | 16 | 16 | 1 | 2
16 | 4 | 10 | 15 | 15 | -1 | 0 | 3
17 | 1 | 15 | 7 | 15 | 16 | 1 | 0
18 | 2 | 15 | 7 | 16 | 9 | 1 | 1
19 | 3 | 15 | 7 | 11 | 8 | 1 | 2
20 | 4 | 15 | 7 | 7 | -1 | 0 | 3
21 | 1 | 15 | 10 | 15 | 3 | 1 | 0
22 | 2 | 15 | 10 | 10 | -1 | 0 | 1
(22 rows)
- Ejemplo:
Manualmente asignar combinaciones de vértices.
SELECT * FROM pgr_Dijkstra(
'SELECT id, source, target, cost, reverse_cost FROM edges',
'SELECT * FROM (VALUES (6, 10), (6, 7), (12, 10)) AS combinations (source, target)');
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 7 | 6 | 4 | 1 | 0
2 | 2 | 6 | 7 | 7 | -1 | 0 | 1
3 | 1 | 6 | 10 | 6 | 4 | 1 | 0
4 | 2 | 6 | 10 | 7 | 8 | 1 | 1
5 | 3 | 6 | 10 | 11 | 9 | 1 | 2
6 | 4 | 6 | 10 | 16 | 16 | 1 | 3
7 | 5 | 6 | 10 | 15 | 3 | 1 | 4
8 | 6 | 6 | 10 | 10 | -1 | 0 | 5
9 | 1 | 12 | 10 | 12 | 13 | 1 | 0
10 | 2 | 12 | 10 | 17 | 15 | 1 | 1
11 | 3 | 12 | 10 | 16 | 16 | 1 | 2
12 | 4 | 12 | 10 | 15 | 3 | 1 | 3
13 | 5 | 12 | 10 | 10 | -1 | 0 | 4
(13 rows)
Los ejemplos de esta sección se basan en la red Datos Muestra.
Para grafos dirigidos con columnas cost and reverse_cost¶
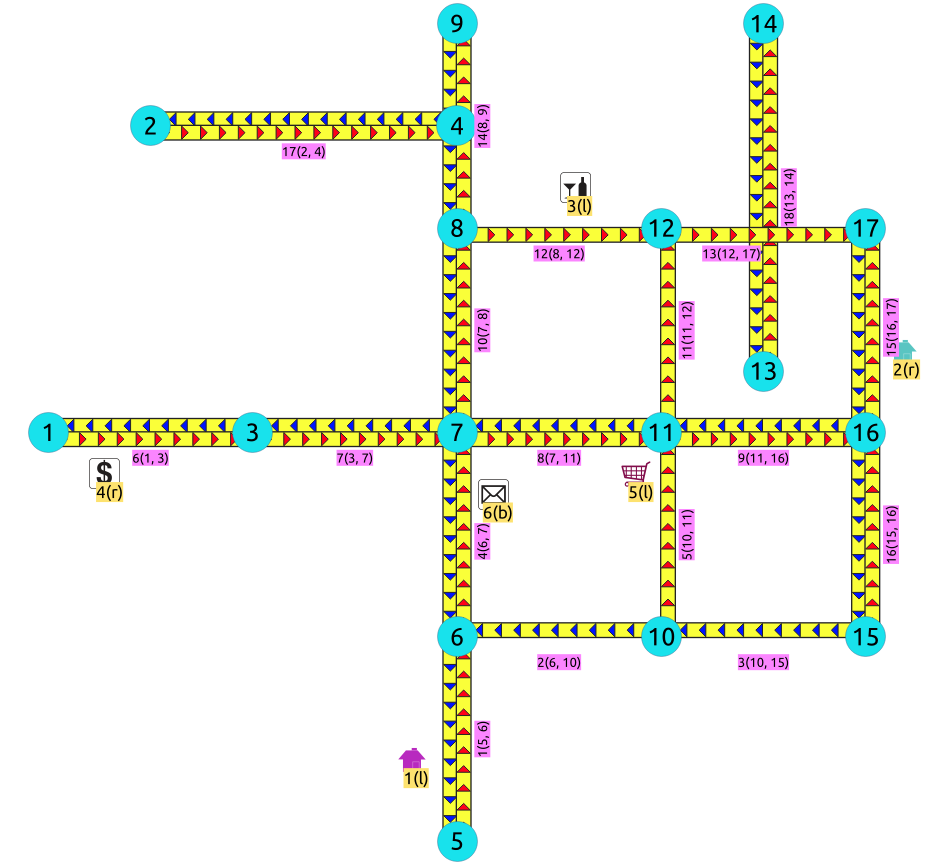
Grafo dirigido con columnas de costo y costo de regreso¶
1) Ruta de \(6\) a \(10\)¶
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost, reverse_cost FROM edges',
6, 10
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 10 | 6 | 4 | 1 | 0
2 | 2 | 6 | 10 | 7 | 8 | 1 | 1
3 | 3 | 6 | 10 | 11 | 9 | 1 | 2
4 | 4 | 6 | 10 | 16 | 16 | 1 | 3
5 | 5 | 6 | 10 | 15 | 3 | 1 | 4
6 | 6 | 6 | 10 | 10 | -1 | 0 | 5
(6 rows)
2) Ruta de \(6\) a \(7\)¶
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost, reverse_cost FROM edges',
6, 7
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 7 | 6 | 4 | 1 | 0
2 | 2 | 6 | 7 | 7 | -1 | 0 | 1
(2 rows)
3) Ruta de \(12\) a \(10\)¶
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost, reverse_cost FROM edges',
12, 10
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 12 | 10 | 12 | 13 | 1 | 0
2 | 2 | 12 | 10 | 17 | 15 | 1 | 1
3 | 3 | 12 | 10 | 16 | 16 | 1 | 2
4 | 4 | 12 | 10 | 15 | 3 | 1 | 3
5 | 5 | 12 | 10 | 10 | -1 | 0 | 4
(5 rows)
4) Ruta de \(12\) a \(7\)¶
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost, reverse_cost FROM edges',
12, 7
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 12 | 7 | 12 | 13 | 1 | 0
2 | 2 | 12 | 7 | 17 | 15 | 1 | 1
3 | 3 | 12 | 7 | 16 | 9 | 1 | 2
4 | 4 | 12 | 7 | 11 | 8 | 1 | 3
5 | 5 | 12 | 7 | 7 | -1 | 0 | 4
(5 rows)
5) Usando Uno a Muchos para obtener la solución de los ejemplos 1 y 2¶
Rutas \(\{6\}\rightarrow\{10, 7\}\)
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost, reverse_cost FROM edges',
6, ARRAY[10, 7]
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 7 | 6 | 4 | 1 | 0
2 | 2 | 6 | 7 | 7 | -1 | 0 | 1
3 | 1 | 6 | 10 | 6 | 4 | 1 | 0
4 | 2 | 6 | 10 | 7 | 8 | 1 | 1
5 | 3 | 6 | 10 | 11 | 9 | 1 | 2
6 | 4 | 6 | 10 | 16 | 16 | 1 | 3
7 | 5 | 6 | 10 | 15 | 3 | 1 | 4
8 | 6 | 6 | 10 | 10 | -1 | 0 | 5
(8 rows)
6) Usando Muchos a Uno para obtener la solución de los ejemplos 2 y 4¶
Rutas \(\{6, 12\}\rightarrow\{7\}\)
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost, reverse_cost FROM edges',
ARRAY[6, 12], 7
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 7 | 6 | 4 | 1 | 0
2 | 2 | 6 | 7 | 7 | -1 | 0 | 1
3 | 1 | 12 | 7 | 12 | 13 | 1 | 0
4 | 2 | 12 | 7 | 17 | 15 | 1 | 1
5 | 3 | 12 | 7 | 16 | 9 | 1 | 2
6 | 4 | 12 | 7 | 11 | 8 | 1 | 3
7 | 5 | 12 | 7 | 7 | -1 | 0 | 4
(7 rows)
7) Usando Muchos a Muchos para obtener la solución de los ejemplos 1 y 4¶
Rutas \(\{6, 12\}\rightarrow\{10, 7\}\)
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost, reverse_cost FROM edges',
ARRAY[6, 12], ARRAY[10,7]
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 7 | 6 | 4 | 1 | 0
2 | 2 | 6 | 7 | 7 | -1 | 0 | 1
3 | 1 | 6 | 10 | 6 | 4 | 1 | 0
4 | 2 | 6 | 10 | 7 | 8 | 1 | 1
5 | 3 | 6 | 10 | 11 | 9 | 1 | 2
6 | 4 | 6 | 10 | 16 | 16 | 1 | 3
7 | 5 | 6 | 10 | 15 | 3 | 1 | 4
8 | 6 | 6 | 10 | 10 | -1 | 0 | 5
9 | 1 | 12 | 7 | 12 | 13 | 1 | 0
10 | 2 | 12 | 7 | 17 | 15 | 1 | 1
11 | 3 | 12 | 7 | 16 | 9 | 1 | 2
12 | 4 | 12 | 7 | 11 | 8 | 1 | 3
13 | 5 | 12 | 7 | 7 | -1 | 0 | 4
14 | 1 | 12 | 10 | 12 | 13 | 1 | 0
15 | 2 | 12 | 10 | 17 | 15 | 1 | 1
16 | 3 | 12 | 10 | 16 | 16 | 1 | 2
17 | 4 | 12 | 10 | 15 | 3 | 1 | 3
18 | 5 | 12 | 10 | 10 | -1 | 0 | 4
(18 rows)
8) Usando Combinaciones para obtener la solución de los ejemplos 1 a 3¶
Rutas \(\{6\}\rightarrow\{10, 7\}\cup\{12\}\rightarrow\{10\}\)
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost, reverse_cost FROM edges',
'SELECT * FROM (VALUES (6, 10), (6, 7), (12, 10)) AS combinations (source, target)'
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 7 | 6 | 4 | 1 | 0
2 | 2 | 6 | 7 | 7 | -1 | 0 | 1
3 | 1 | 6 | 10 | 6 | 4 | 1 | 0
4 | 2 | 6 | 10 | 7 | 8 | 1 | 1
5 | 3 | 6 | 10 | 11 | 9 | 1 | 2
6 | 4 | 6 | 10 | 16 | 16 | 1 | 3
7 | 5 | 6 | 10 | 15 | 3 | 1 | 4
8 | 6 | 6 | 10 | 10 | -1 | 0 | 5
9 | 1 | 12 | 10 | 12 | 13 | 1 | 0
10 | 2 | 12 | 10 | 17 | 15 | 1 | 1
11 | 3 | 12 | 10 | 16 | 16 | 1 | 2
12 | 4 | 12 | 10 | 15 | 3 | 1 | 3
13 | 5 | 12 | 10 | 10 | -1 | 0 | 4
(13 rows)
Para grafos no dirigidos con columnas cost y reverse_cost¶
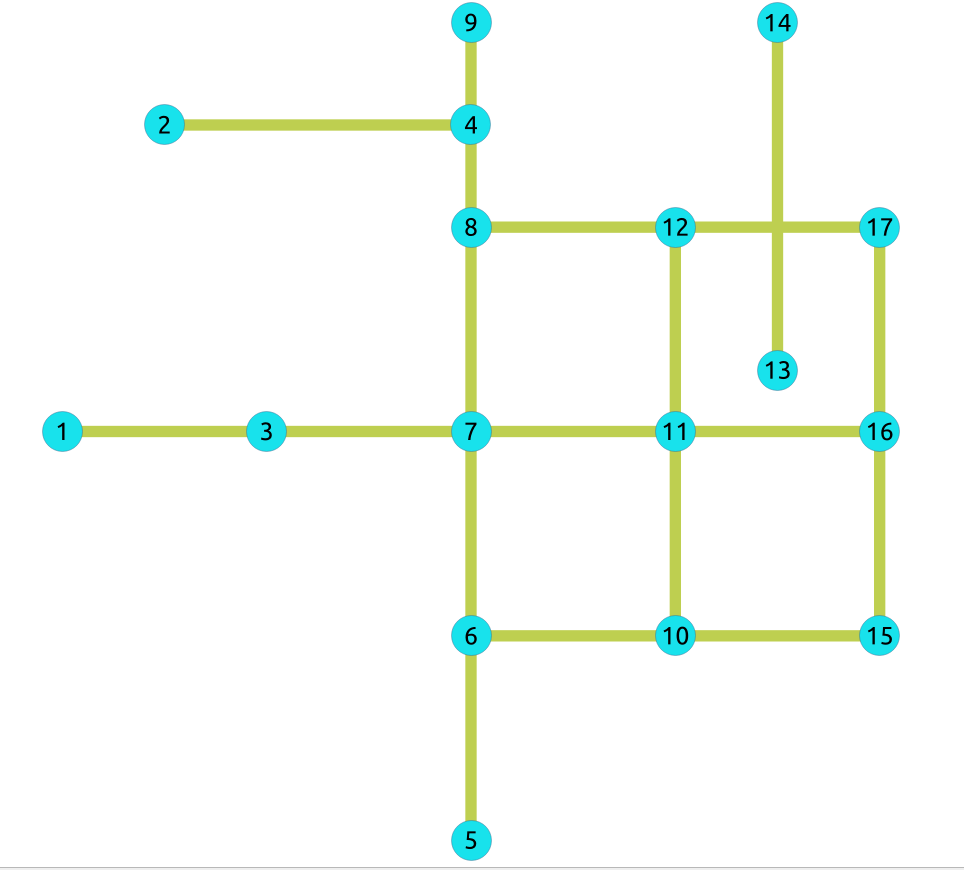
Grafo no dirigido con columnas de costo y costo de regreso¶
9) Ruta de \(6\) a \(10\)¶
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost, reverse_cost FROM edges',
6, 10,
false
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 10 | 6 | 2 | 1 | 0
2 | 2 | 6 | 10 | 10 | -1 | 0 | 1
(2 rows)
10) Ruta de \(6\) a \(7\)¶
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost, reverse_cost FROM edges',
6, 7,
false
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 7 | 6 | 4 | 1 | 0
2 | 2 | 6 | 7 | 7 | -1 | 0 | 1
(2 rows)
11) Ruta de \(12\) a \(10\)¶
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost, reverse_cost FROM edges',
12, 10,
false
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 12 | 10 | 12 | 11 | 1 | 0
2 | 2 | 12 | 10 | 11 | 5 | 1 | 1
3 | 3 | 12 | 10 | 10 | -1 | 0 | 2
(3 rows)
12) Ruta de \(12\) a \(7\)¶
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost, reverse_cost FROM edges',
12, 7,
false
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 12 | 7 | 12 | 12 | 1 | 0
2 | 2 | 12 | 7 | 8 | 10 | 1 | 1
3 | 3 | 12 | 7 | 7 | -1 | 0 | 2
(3 rows)
13) Usando Uno a Muchos para obtener la solución de los ejemplos 9 y 10¶
Rutas \(\{6\}\rightarrow\{10, 7\}\)
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost, reverse_cost FROM edges',
6, ARRAY[10,7],
false
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 7 | 6 | 4 | 1 | 0
2 | 2 | 6 | 7 | 7 | -1 | 0 | 1
3 | 1 | 6 | 10 | 6 | 2 | 1 | 0
4 | 2 | 6 | 10 | 10 | -1 | 0 | 1
(4 rows)
14) Usando Muchos a Uno para obtener la solución de los ejemplos 10 y 12¶
Rutas \(\{6, 12\}\rightarrow\{7\}\)
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost, reverse_cost FROM edges',
ARRAY[6,12], 7,
false
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 7 | 6 | 4 | 1 | 0
2 | 2 | 6 | 7 | 7 | -1 | 0 | 1
3 | 1 | 12 | 7 | 12 | 12 | 1 | 0
4 | 2 | 12 | 7 | 8 | 10 | 1 | 1
5 | 3 | 12 | 7 | 7 | -1 | 0 | 2
(5 rows)
15) Usando Muchos a Muchos para obtener la solución de los ejemplos 9 y 12¶
Rutas \(\{6, 12\}\rightarrow\{10, 7\}\)
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost, reverse_cost FROM edges',
ARRAY[6, 12], ARRAY[10,7],
false
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 7 | 6 | 4 | 1 | 0
2 | 2 | 6 | 7 | 7 | -1 | 0 | 1
3 | 1 | 6 | 10 | 6 | 2 | 1 | 0
4 | 2 | 6 | 10 | 10 | -1 | 0 | 1
5 | 1 | 12 | 7 | 12 | 12 | 1 | 0
6 | 2 | 12 | 7 | 8 | 10 | 1 | 1
7 | 3 | 12 | 7 | 7 | -1 | 0 | 2
8 | 1 | 12 | 10 | 12 | 11 | 1 | 0
9 | 2 | 12 | 10 | 11 | 5 | 1 | 1
10 | 3 | 12 | 10 | 10 | -1 | 0 | 2
(10 rows)
16) Usando Combinaciones para obtener la solución de los ejemplos 9 a 13¶
Rutas \(\{6\}\rightarrow\{10, 7\}\cup\{12\}\rightarrow\{10\}\)
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost, reverse_cost FROM edges',
'SELECT * FROM (VALUES (6, 10), (6, 7), (12, 10)) AS combinations (source, target)',
false
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 7 | 6 | 4 | 1 | 0
2 | 2 | 6 | 7 | 7 | -1 | 0 | 1
3 | 1 | 6 | 10 | 6 | 2 | 1 | 0
4 | 2 | 6 | 10 | 10 | -1 | 0 | 1
5 | 1 | 12 | 10 | 12 | 11 | 1 | 0
6 | 2 | 12 | 10 | 11 | 5 | 1 | 1
7 | 3 | 12 | 10 | 10 | -1 | 0 | 2
(7 rows)
Para grafos dirigidos con columna``cost``¶
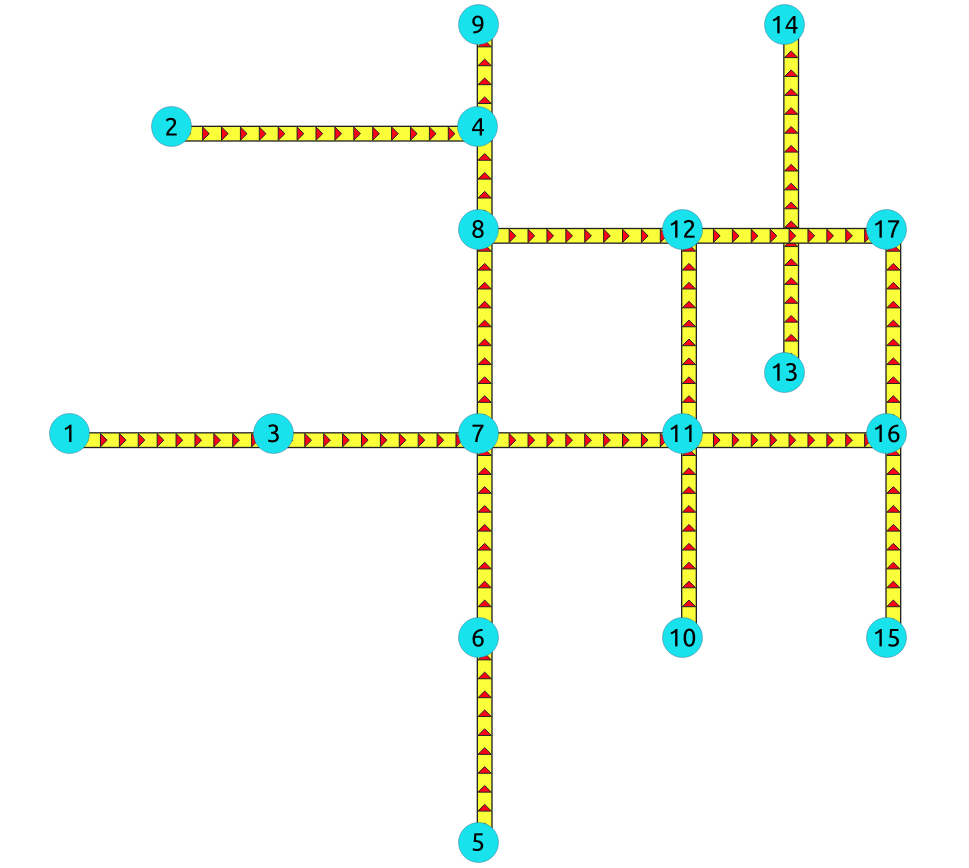
Grafo dirigido con solo la columna costo¶
17) Ruta de \(6\) a \(10\)¶
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost FROM edges',
6, 10
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
(0 rows)
18) Ruta de \(6\) a \(7\)¶
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost FROM edges',
6, 7
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 7 | 6 | 4 | 1 | 0
2 | 2 | 6 | 7 | 7 | -1 | 0 | 1
(2 rows)
19) Ruta de \(12\) a \(10\)¶
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost FROM edges',
12, 10
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
(0 rows)
20) Ruta de \(12\) a \(7\)¶
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost FROM edges',
12, 7
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
(0 rows)
21) Usando Uno a Muchos para obtener la solución de los ejemplos 17 y 18¶
Rutas \(\{6\}\rightarrow\{10, 7\}\)
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost FROM edges',
6, ARRAY[10,7]
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 7 | 6 | 4 | 1 | 0
2 | 2 | 6 | 7 | 7 | -1 | 0 | 1
(2 rows)
22) Usando Muchos a Uno para obtener la solución de los ejemplos 18 y 20¶
Rutas \(\{6, 12\}\rightarrow\{7\}\)
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost FROM edges',
ARRAY[6,12], 7
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 7 | 6 | 4 | 1 | 0
2 | 2 | 6 | 7 | 7 | -1 | 0 | 1
(2 rows)
23) Usando Muchos a Muchos para obtener la solución de los ejemplos 17 y 20¶
Rutas \(\{6, 12\}\rightarrow\{10, 7\}\)
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost FROM edges',
ARRAY[6, 12], ARRAY[10,7]
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 7 | 6 | 4 | 1 | 0
2 | 2 | 6 | 7 | 7 | -1 | 0 | 1
(2 rows)
24) Usando Combinaciones para obtener la solución de los ejemplos 17 a 19¶
Rutas \(\{6\}\rightarrow\{10, 7\}\cup\{12\}\rightarrow\{10\}\)
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost FROM edges',
'SELECT * FROM (VALUES (6, 10), (6, 7), (12, 10)) AS combinations (source, target)'
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 7 | 6 | 4 | 1 | 0
2 | 2 | 6 | 7 | 7 | -1 | 0 | 1
(2 rows)
Para grafos no dirigidos con columna``cost``¶
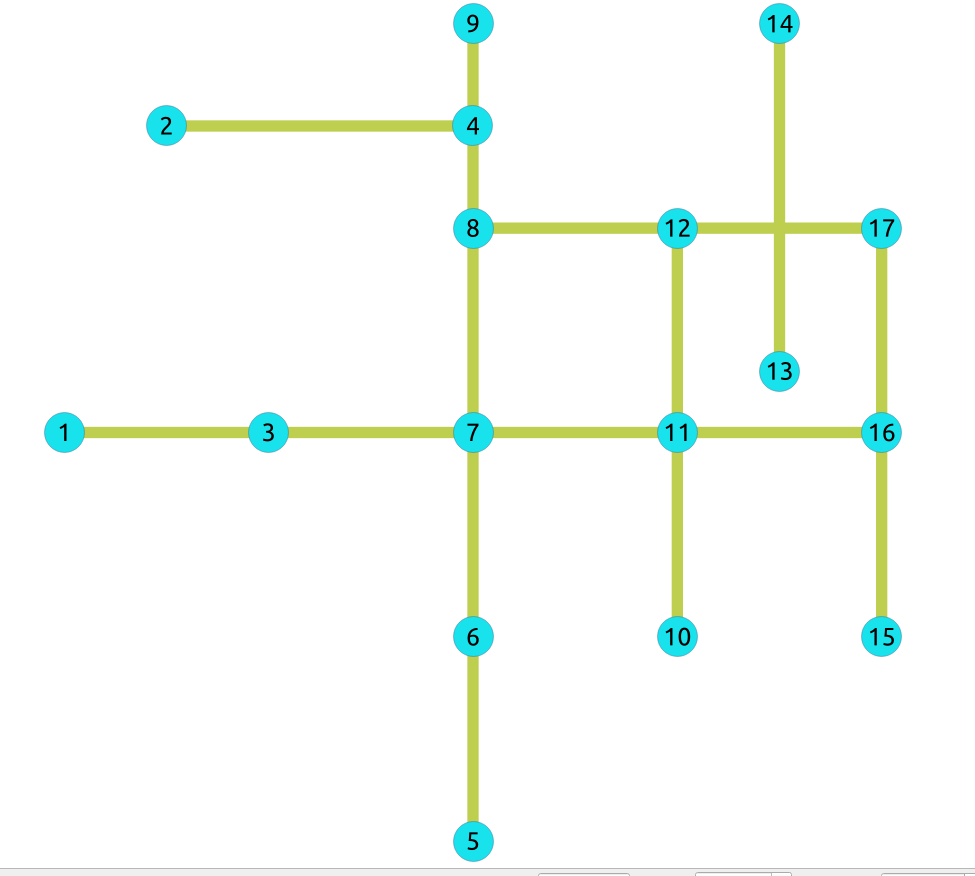
Grafo no dirigido con solo la columna costo¶
25) Ruta de \(6\) a \(10\)¶
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost FROM edges',
6, 10,
false
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 10 | 6 | 4 | 1 | 0
2 | 2 | 6 | 10 | 7 | 8 | 1 | 1
3 | 3 | 6 | 10 | 11 | 5 | 1 | 2
4 | 4 | 6 | 10 | 10 | -1 | 0 | 3
(4 rows)
26) Ruta de \(6\) a \(7\)¶
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost FROM edges',
6, 7,
false
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 7 | 6 | 4 | 1 | 0
2 | 2 | 6 | 7 | 7 | -1 | 0 | 1
(2 rows)
27) Ruta de \(12\) a \(10\)¶
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost FROM edges',
12, 10,
false
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 12 | 10 | 12 | 11 | 1 | 0
2 | 2 | 12 | 10 | 11 | 5 | 1 | 1
3 | 3 | 12 | 10 | 10 | -1 | 0 | 2
(3 rows)
28) Ruta de \(12\) a \(7\)¶
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost FROM edges',
12, 7,
false
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 12 | 7 | 12 | 12 | 1 | 0
2 | 2 | 12 | 7 | 8 | 10 | 1 | 1
3 | 3 | 12 | 7 | 7 | -1 | 0 | 2
(3 rows)
29) Usando Uno a Muchos para obtener la solución de los ejemplos 25 y 26¶
Rutas \(\{6\}\rightarrow\{10, 7\}\)
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost FROM edges',
6, ARRAY[10,7],
false
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 7 | 6 | 4 | 1 | 0
2 | 2 | 6 | 7 | 7 | -1 | 0 | 1
3 | 1 | 6 | 10 | 6 | 4 | 1 | 0
4 | 2 | 6 | 10 | 7 | 8 | 1 | 1
5 | 3 | 6 | 10 | 11 | 5 | 1 | 2
6 | 4 | 6 | 10 | 10 | -1 | 0 | 3
(6 rows)
30) Usando Muchos a Uno para obtener la solución de los ejemplos 26 y 28¶
Rutas \(\{6, 12\}\rightarrow\{7\}\)
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost FROM edges',
ARRAY[6,12], 7,
false
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 7 | 6 | 4 | 1 | 0
2 | 2 | 6 | 7 | 7 | -1 | 0 | 1
3 | 1 | 12 | 7 | 12 | 12 | 1 | 0
4 | 2 | 12 | 7 | 8 | 10 | 1 | 1
5 | 3 | 12 | 7 | 7 | -1 | 0 | 2
(5 rows)
31) Usando Muchos a Muchos para obtener la solución de los ejemplos 25 y 28¶
Rutas \(\{6, 12\}\rightarrow\{10, 7\}\)
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost FROM edges',
ARRAY[6, 12], ARRAY[10,7],
false
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 7 | 6 | 4 | 1 | 0
2 | 2 | 6 | 7 | 7 | -1 | 0 | 1
3 | 1 | 6 | 10 | 6 | 4 | 1 | 0
4 | 2 | 6 | 10 | 7 | 8 | 1 | 1
5 | 3 | 6 | 10 | 11 | 5 | 1 | 2
6 | 4 | 6 | 10 | 10 | -1 | 0 | 3
7 | 1 | 12 | 7 | 12 | 12 | 1 | 0
8 | 2 | 12 | 7 | 8 | 10 | 1 | 1
9 | 3 | 12 | 7 | 7 | -1 | 0 | 2
10 | 1 | 12 | 10 | 12 | 11 | 1 | 0
11 | 2 | 12 | 10 | 11 | 5 | 1 | 1
12 | 3 | 12 | 10 | 10 | -1 | 0 | 2
(12 rows)
32) Usando Combinaciones para obtener la solución de los ejemplos 25 a 27¶
Rutas \(\{6\}\rightarrow\{10, 7\}\cup\{12\}\rightarrow\{10\}\)
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost FROM edges',
'SELECT * FROM (VALUES (6, 10), (6, 7), (12, 10)) AS combinations (source, target)',
false
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 7 | 6 | 4 | 1 | 0
2 | 2 | 6 | 7 | 7 | -1 | 0 | 1
3 | 1 | 6 | 10 | 6 | 4 | 1 | 0
4 | 2 | 6 | 10 | 7 | 8 | 1 | 1
5 | 3 | 6 | 10 | 11 | 5 | 1 | 2
6 | 4 | 6 | 10 | 10 | -1 | 0 | 3
7 | 1 | 12 | 10 | 12 | 11 | 1 | 0
8 | 2 | 12 | 10 | 11 | 5 | 1 | 1
9 | 3 | 12 | 10 | 10 | -1 | 0 | 2
(9 rows)
Equivalencias entre firmas¶
Los siguientes ejemplos son para la ruta \(\{6\}\rightarrow\{10\}\)
33) Usando Uno a Uno¶
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost, reverse_cost FROM edges',
6, 10
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 10 | 6 | 4 | 1 | 0
2 | 2 | 6 | 10 | 7 | 8 | 1 | 1
3 | 3 | 6 | 10 | 11 | 9 | 1 | 2
4 | 4 | 6 | 10 | 16 | 16 | 1 | 3
5 | 5 | 6 | 10 | 15 | 3 | 1 | 4
6 | 6 | 6 | 10 | 10 | -1 | 0 | 5
(6 rows)
34) Usando Uno a Muchos¶
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost, reverse_cost FROM edges',
6, ARRAY[10]
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 10 | 6 | 4 | 1 | 0
2 | 2 | 6 | 10 | 7 | 8 | 1 | 1
3 | 3 | 6 | 10 | 11 | 9 | 1 | 2
4 | 4 | 6 | 10 | 16 | 16 | 1 | 3
5 | 5 | 6 | 10 | 15 | 3 | 1 | 4
6 | 6 | 6 | 10 | 10 | -1 | 0 | 5
(6 rows)
35) Usando Muchos a Uno¶
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost, reverse_cost FROM edges',
ARRAY[6], 10
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 10 | 6 | 4 | 1 | 0
2 | 2 | 6 | 10 | 7 | 8 | 1 | 1
3 | 3 | 6 | 10 | 11 | 9 | 1 | 2
4 | 4 | 6 | 10 | 16 | 16 | 1 | 3
5 | 5 | 6 | 10 | 15 | 3 | 1 | 4
6 | 6 | 6 | 10 | 10 | -1 | 0 | 5
(6 rows)
36) Usando Muchos a Muchos¶
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost, reverse_cost FROM edges',
ARRAY[6], ARRAY[10]
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 10 | 6 | 4 | 1 | 0
2 | 2 | 6 | 10 | 7 | 8 | 1 | 1
3 | 3 | 6 | 10 | 11 | 9 | 1 | 2
4 | 4 | 6 | 10 | 16 | 16 | 1 | 3
5 | 5 | 6 | 10 | 15 | 3 | 1 | 4
6 | 6 | 6 | 10 | 10 | -1 | 0 | 5
(6 rows)
37) Usando Combinaciones¶
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost, reverse_cost FROM edges',
'SELECT * FROM (VALUES(6, 10)) AS combinations (source, target)'
);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 10 | 6 | 4 | 1 | 0
2 | 2 | 6 | 10 | 7 | 8 | 1 | 1
3 | 3 | 6 | 10 | 11 | 9 | 1 | 2
4 | 4 | 6 | 10 | 16 | 16 | 1 | 3
5 | 5 | 6 | 10 | 15 | 3 | 1 | 4
6 | 6 | 6 | 10 | 10 | -1 | 0 | 5
(6 rows)
Ver también¶
Las consultas utilizan la red Datos Muestra .
Índices y tablas