Unsupported versions:2.6 2.5 2.4 2.3 2.2 2.1 2.0
pgRouting 基本概念¶
这是一个简单的指南,介绍了 pgRouting 入门的一些步骤。 本指南涵盖:
图¶
图定义¶
图是一个有序对
有不同类型的图:
无向图
无向简单图
有向图
有向简单图
图:
没有几何图形。
一些图论问题需要图具有权重,在 pgRouting 中称为 成本 。
在 pgRouting 中,有多种方法来表示数据库上的图:
使用
cost(
id,source,target,cost)
使用
cost和reverse_cost(
id,source,target,cost,reverse_cost)
其中:
列 |
描述 |
|---|---|
|
边的标识符。要求在数据库中以一致的方式使用。 |
|
顶点的标识符。 |
|
顶点的标识符。 |
|
边 (
|
|
边(
|
图是 有向 图还是 无向 图的决定是在执行 pgRouting 算法时完成的。
成本 图¶
加权有向图,
通过查询获取图数据
SELECT id, source, target, cost FROM edges边集
成本非负的边是图的一部分。
顶点集
source和``target`` 中的所有顶点都是图的一部分。
有向图
在有向图中,边
对于以下数据:
SELECT *
FROM (VALUES (1, 1, 2, 5), (2, 1, 3, -3))
AS t(id, source, target, cost);
id | source | target | cost
----+--------+--------+------
1 | 1 | 2 | 5
2 | 1 | 3 | -3
(2 rows)
边
数据代表下图:
![digraph G {
1 -> 2 [label="1(5)"];
3;
}](_images/graphviz-6a22e17e4c49cbe911a2c3c04aea2e93942005ce.png)
无向图
在无向图中,边
在有向图的术语中,这相当于有两条边:
对于以下数据:
SELECT *
FROM (VALUES (1, 1, 2, 5), (2, 1, 3, -3))
AS t(id, source, target, cost);
id | source | target | cost
----+--------+--------+------
1 | 1 | 2 | 5
2 | 1 | 3 | -3
(2 rows)
边
数据代表下图:
![graph G {
1 -- 2 [label="1(5)"];
3;
}](_images/graphviz-a9ff7d505ee3aa8158a1f3439d4325a71f0dbcae.png)
带有 cost 和``reverse_cost`` 的图¶
加权有向图,
通过查询获取图数据
SELECT id, source, target, cost, reverse_cost FROM edges边的集合
边
cost是非负数的都属于图的一部分。边
reverse_cost是非负数的都属于图的一部分。
顶点集
source和``target`` 中的所有顶点都是图的一部分。
有向图
在有向图中,两条边都有方向性
边
边
对于以下数据:
SELECT *
FROM (VALUES (1, 1, 2, 5, 2), (2, 1, 3, -3, 4), (3, 2, 3, 7, -1))
AS t(id, source, target, cost, reverse_cost);
id | source | target | cost | reverse_cost
----+--------+--------+------+--------------
1 | 1 | 2 | 5 | 2
2 | 1 | 3 | -3 | 4
3 | 2 | 3 | 7 | -1
(3 rows)
边不是图的一部分:
数据代表下图:
![digraph G {
1 -> 2 [label="1(5)"];
2 -> 1 [label="1(2)"];
3 -> 1 [label="2(4)"];
2 -> 3 [label="3(7)"];
}](_images/graphviz-cf2723f26bd1c3ee60f314423c76e21eb5708d4e.png)
无向图
在有向图中,两条边都没有方向性
边
边
就有向图而言,就像有四个边:
对于以下数据:
SELECT *
FROM (VALUES (1, 1, 2, 5, 2), (2, 1, 3, -3, 4), (3, 2, 3, 7, -1))
AS t(id, source, target, cost, reverse_cost);
id | source | target | cost | reverse_cost
----+--------+--------+------+--------------
1 | 1 | 2 | 5 | 2
2 | 1 | 3 | -3 | 4
3 | 2 | 3 | 7 | -1
(3 rows)
边不是图的一部分:
数据代表下图:
![graph G {
1 -- 2 [label="1(5)"];
2 -- 1 [label="1(2)"];
3 -- 1 [label="2(4)"];
2 -- 3 [label="3(7)"];
}](_images/graphviz-7cf300b7d69445756b30b2135af90e936a5dd9e4.png)
没有几何信息的图¶
使用 pgRouting 可以解决个人关系、家谱和文件依赖性问题。这些问题通常不会与图形相关的几何图形一起出现。
维基示例¶
解决来自 维基百科 )的示例问题 :
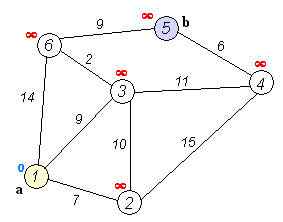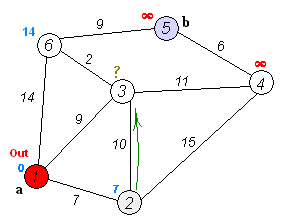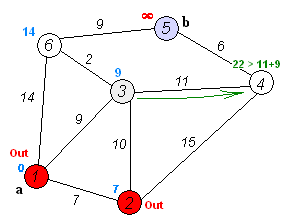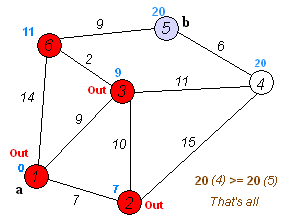
其中:
问题是找到从
是一个无向图。
虽然视觉上看起来有几何形状,但该图并不是按比例绘制的。
没有与顶点或边关联的几何图形
有6个顶点
有九个边:
该图可以用多种方式表示,例如:
![graph G {
rankdir="LR";
1 [color="red"];
5 [color="green"];
1 -- 2 [label="(7)"];
5 -- 6 [label="(9)"];
1 -- 3 [label="(9)"];
1 -- 6 [label="(14)"];
2 -- 3 [label="(10)"];
2 -- 4 [label="(13)"];
3 -- 4 [label="(11)"];
3 -- 6 [label="(2)"];
4 -- 5 [label="(6)"];
}](_images/graphviz-aa83b370a30d7a5c2be123929174e31044bca152.png)
准备数据库¶
为示例创建一个数据库,访问数据库并安装 pgRouting::
$ createdb wiki
$ psql wiki
wiki =# CREATE EXTENSION pgRouting CASCADE;
创建表¶
在无向图上执行基本路由所需的基本元素是:
列 |
类型 |
描述 |
|---|---|---|
|
ANY-INTEGER |
边的标识符。 |
|
ANY-INTEGER |
边的第一个端点顶点的标识符。 |
|
ANY-INTEGER |
边的第二个端点顶点的标识符。 |
|
ANY-NUMERICAL |
边( |
其中:
- ANY-INTEGER:
SMALLINT, INTEGER, BIGINT
- ANY-NUMERICAL:
SMALLINT, INTEGER, BIGINT, REAL, FLOAT
本示例使用此表设计:
CREATE TABLE wiki (
id SERIAL,
source INTEGER,
target INTEGER,
cost INTEGER);
CREATE TABLE
插入数据¶
INSERT INTO wiki (source, target, cost) VALUES
(1, 2, 7), (1, 3, 9), (1, 6, 14),
(2, 3, 10), (2, 4, 15),
(3, 6, 2), (3, 4, 11),
(4, 5, 6),
(5, 6, 9);
INSERT 0 9
寻找最短路径¶
为了解决这个例子,使用了 pgr_dijkstra`:
SELECT * FROM pgr_dijkstra(
'SELECT id, source, target, cost FROM wiki',
1, 5, false);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 1 | 5 | 1 | 2 | 9 | 0
2 | 2 | 1 | 5 | 3 | 6 | 2 | 9
3 | 3 | 1 | 5 | 6 | 9 | 9 | 11
4 | 4 | 1 | 5 | 5 | -1 | 0 | 20
(4 rows)
从
![graph G {
rankdir="LR";
1 [color="red"];
5 [color="green"];
1 -- 2 [label="(7)"];
5 -- 6 [label="(9)", color="blue"];
1 -- 3 [label="(9)", color="blue"];
1 -- 6 [label="(14)"];
2 -- 3 [label="(10)"];
2 -- 4 [label="(13)"];
3 -- 4 [label="(11)"];
3 -- 6 [label="(2)", color="blue"];
4 -- 5 [label="(6)"];
}](_images/graphviz-2be84fbb8166d4e067f5592a16b83c30776ea85c.png)
顶点信息¶
要获取顶点信息,请使用 pgr_extractVertices
SELECT id, in_edges, out_edges
FROM pgr_extractVertices('SELECT id, source, target FROM wiki');
id | in_edges | out_edges
----+----------+-----------
3 | {2,4} | {6,7}
5 | {8} | {9}
4 | {5,7} | {8}
2 | {1} | {4,5}
1 | | {1,2,3}
6 | {3,6,9} |
(6 rows)
具有几何图形的图¶
创建路由数据库¶
第一步是创建数据库并在数据库中加载 pgRouting。
通常为每个项目创建一个数据库。
一旦数据库可以工作,加载数据并在该数据库中构建路由应用程序。
createdb sampledata
psql sampledata -c "CREATE EXTENSION pgrouting CASCADE"
加载数据¶
有多种方法可以将数据加载到 pgRouting 中。
手动创建数据库。
有多种开源工具可以提供帮助,例如:
- shp2pgsql:
postgresql shapefile 加载器
- ogr2ogr:
矢量数据转换实用程序
- osm2pgsql:
将OSM数据加载到postgresql中
请注意,这些工具 不会 导入与 pgRouting 兼容的结构中的数据,当发生这种情况时,需要调整拓扑。
在每个线段-线段交叉点上分解线段
如果缺少,请添加列并为
source,target,cost,reverse_cost分配值。连接断开的图。
创建完整的图拓扑
根据要开发的应用程序创建一个或多个图。
为高速道路创建收缩图
创建每个州/国家的图
简而言之:
准备图
准备什么以及如何准备图将取决于应用程序和/或数据质量和/或信息与 pgRouting 可用的拓扑的接近程度和/或未提及的一些其他因素。
准备图的步骤涉及使用`PostGIS <https://postgis.net/>`__ 进行几何操作,其他一些步骤涉及诸如 pgr_contraction 之类的图操作来收缩图。
该 workshop 逐步介绍了如何使用开放街道地图数据为小型应用程序准备图。
数据库设计上索引的使用一般:
对几何图形进行索引。
对标识符列建立索引。
请查阅`PostgreSQL <https://www.postgresql.org/docs/>`__ 文档和 PostGIS 文档。
构建路由拓扑¶
使用大多数 pgRouting 函数的基本信息``id, source, target, cost, [reverse_cost]`` 在 pgRouting 中被称为路由拓扑。
reverse_cost 是可选的,但强烈建议使用,以便由于几何列的大小而减小数据库的大小。 话虽如此,在本文档中使用了 reverse_cost。
当数据带有几何图形并且没有路由拓扑时,则需要此步骤。
几何图的所有开始和结束顶点都需要一个标识符,该标识符将存储在数据表的``source``列和``target``列中。 同样,cost 和 reverse_cost 需要具有在两个方向上遍历边的值。
如果这些列不存在,则需要将它们添加到相关表中。 (参见`ALTER TABLE <https://www.postgresql.org/docs/current/sql-altertable.html>`__ )
函数 pgr_extractVertices 用于根据边标识符和图边的几何形状创建顶点表。
SELECT * INTO vertices
FROM pgr_extractVertices('SELECT id, geom FROM edges ORDER BY id');
SELECT 18
最后使用存储在顶点表上的数据填充 source 和``target``。
/* -- set the source information */
UPDATE edges AS e
SET source = v.id, x1 = x, y1 = y
FROM vertices AS v
WHERE ST_StartPoint(e.geom) = v.geom;
UPDATE 24
/* -- set the target information */
UPDATE edges AS e
SET target = v.id, x2 = x, y2 = y
FROM vertices AS v
WHERE ST_EndPoint(e.geom) = v.geom;
UPDATE 24
来自 OSM 并使用 osm2pgrouting 作为导入工具的数据附带路由拓扑。 请参阅 workshop 上使用 osm2pgrouting 的示例。
调整成本¶
对于本示例, cost 和 reverse_cost 值将是几何体长度的两倍。
将成本更新为几何形状的长度¶
假设样本数据中的 cost 和 reverse_cost 列表示:
当边存在于图中时为
当图中不存在边时为
使用该信息更新几何形状的长度:
UPDATE edges SET
cost = sign(cost) * ST_length(geom) * 2,
reverse_cost = sign(reverse_cost) * ST_length(geom) * 2;
UPDATE 18
给出以下结果:
SELECT id, cost, reverse_cost FROM edges;
id | cost | reverse_cost
----+--------------------+--------------------
6 | 2 | 2
7 | 2 | 2
4 | 2 | 2
5 | 2 | -2
8 | 2 | 2
12 | 2 | -2
11 | 2 | -2
10 | 2 | 2
17 | 2.999999999998 | 2.999999999998
14 | 2 | 2
18 | 3.4000000000000004 | 3.4000000000000004
13 | 2 | -2
15 | 2 | 2
16 | 2 | 2
9 | 2 | 2
3 | -2 | 2
1 | 2 | 2
2 | -2 | 2
(18 rows)
请注意,为了能够遵循文档示例,一切都基于原始图。
回到原始数据:
UPDATE edges SET
cost = sign(cost),
reverse_cost = sign(reverse_cost);
UPDATE 18
根据代码更新成本¶
其他数据集可以有一列包含如下值
FT几何方向上的车流TF车流与几何方向相反B双向车流
为示例准备代码列:
ALTER TABLE edges ADD COLUMN direction TEXT;
ALTER TABLE
UPDATE edges SET
direction = CASE WHEN (cost>0 AND reverse_cost>0) THEN 'B' /* both ways */
WHEN (cost>0 AND reverse_cost<0) THEN 'FT' /* direction of the LINESSTRING */
WHEN (cost<0 AND reverse_cost>0) THEN 'TF' /* reverse direction of the LINESTRING */
ELSE '' END;
UPDATE 18
/* unknown */
根据代码调整成本:
UPDATE edges SET
cost = CASE WHEN (direction = 'B' OR direction = 'FT')
THEN ST_length(geom) * 2
ELSE -1 END,
reverse_cost = CASE WHEN (direction = 'B' OR direction = 'TF')
THEN ST_length(geom) * 2
ELSE -1 END;
UPDATE 18
给出以下结果:
SELECT id, cost, reverse_cost FROM edges;
id | cost | reverse_cost
----+--------------------+--------------------
6 | 2 | 2
7 | 2 | 2
4 | 2 | 2
5 | 2 | -1
8 | 2 | 2
12 | 2 | -1
11 | 2 | -1
10 | 2 | 2
17 | 2.999999999998 | 2.999999999998
14 | 2 | 2
18 | 3.4000000000000004 | 3.4000000000000004
13 | 2 | -1
15 | 2 | 2
16 | 2 | 2
9 | 2 | 2
3 | -1 | 2
1 | 2 | 2
2 | -1 | 2
(18 rows)
回到原始数据:
UPDATE edges SET
cost = sign(cost),
reverse_cost = sign(reverse_cost);
UPDATE 18
ALTER TABLE edges DROP COLUMN direction;
ALTER TABLE
检查路由拓扑¶
图中可能存在很多问题。
使用的数据在设计时可能没有考虑路由。
图有一些非常具体的要求。
该图已断开连接。
存在不需要的交叉点。
图太大,需要收缩。
该应用程序需要一个子图。
以及 pgRouting 用户(即应用程序开发人员)可能遇到的许多其他问题。
交叉边¶
要获取交叉边:
SELECT a.id, b.id
FROM edges AS a, edges AS b
WHERE a.id < b.id AND st_crosses(a.geom, b.geom);
id | id
----+----
13 | 18
(1 row)
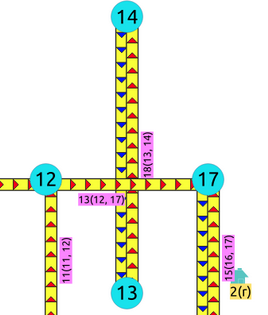
这些信息是正确的,例如,就车辆而言,是隧道还是横跨另一条道路的桥梁。
它可能是不正确的,例如:
当它实际上是道路交叉口时,车辆可以转弯。
在电力线路方面,电力线能够在隧道或桥梁上甚至切换道路。
当不正确时,需要修复:
对于车辆和行人
如果数据来自 OSM 并使用
osm2pgrouting导入到数据库,则需要在 OSM portal 中完成修复并再次导入数据。一般来说,当数据来自为车辆路线准备数据的供应商时,并且出现问题时,需要从供应商处修复数据
对于非常具体的应用
从路线车辆或行人的角度来看,数据是正确的。
数据需要针对特定应用程序进行本地修复。
对交叉点进行一一分析后,对于需要局部修复的交叉点,需要 分割 边。
需要将新边添加到边表中,需要更新新边中的其余属性,需要删除旧边并需要更新路由拓扑。
Fixing an intersection¶
In this example the original edge table will be used to store the additional geometries.
An example use without results
Routing from
SELECT *
FROM pgr_dijkstra('SELECT id, source, target, cost, reverse_cost FROM edges', 1, 18);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
(0 rows)
Analyze the network for intersections.
SELECT
e1.id id1, e2.id id2,
ST_AsText(ST_Intersection(e1.geom, e2.geom)) AS point
FROM edges e1, edges e2
WHERE e1.id < e2.id AND ST_Crosses(e1.geom, e2.geom);
id1 | id2 | point
-----+-----+--------------
13 | 18 | POINT(3.5 3)
(1 row)
The analysis tell us that the network has an intersection.
Prepare tables
Additional columns to control the origin of the segments.
ALTER TABLE edges ADD old_id BIGINT;
ALTER TABLE
Adding new segments.
Calling pgr_separateCrossing and adding the new segments to the edges table.
INSERT INTO edges (old_id, geom)
SELECT id, geom
FROM pgr_separateCrossing('SELECT id, geom FROM edges');
INSERT 0 4
Update other values
In this example only cost and reverse_cost are updated, where they are
based on the length of the geometry and the directionality is kept using the
sign function.
WITH
costs AS (
SELECT e2.id, sign(e1.cost) * ST_Length(e2.geom) AS cost,
sign(e1.reverse_cost) * ST_Length(e2.geom) AS reverse_cost
FROM edges e1 JOIN edges e2 ON (e1.id = e2.old_id)
)
UPDATE edges e
SET (cost, reverse_cost) = (c.cost, c.reverse_cost)
FROM costs AS c WHERE e.id = c.id;
UPDATE 4
Update the topology
Insert the new vertices if any.
WITH
new_vertex AS (
SELECT ev.*
FROM pgr_extractVertices('SELECT id, geom FROM edges WHERE old_id IS NOT NULL') ev
LEFT JOIN vertices v using(geom)
WHERE v IS NULL)
INSERT INTO vertices (in_edges, out_edges,x,y,geom)
SELECT in_edges, out_edges,x,y,geom FROM new_vertex;
INSERT 0 1
Update source and target information on the edges table.
/* -- set the source information */
UPDATE edges AS e
SET source = v.id, x1 = x, y1 = y
FROM vertices AS v
WHERE source IS NULL AND ST_StartPoint(e.geom) = v.geom;
UPDATE 4
/* -- set the target information */
UPDATE edges AS e
SET target = v.id, x2 = x, y2 = y
FROM vertices AS v
WHERE target IS NULL AND ST_EndPoint(e.geom) = v.geom;
UPDATE 4
The example has results
Routing from
SELECT *
FROM pgr_dijkstra('SELECT id, source, target, cost, reverse_cost FROM edges', 1, 18);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 1 | 18 | 1 | 6 | 1 | 0
2 | 2 | 1 | 18 | 3 | 7 | 1 | 1
3 | 3 | 1 | 18 | 7 | 10 | 1 | 2
4 | 4 | 1 | 18 | 8 | 12 | 1 | 3
5 | 5 | 1 | 18 | 12 | 19 | 0.5 | 4
6 | 6 | 1 | 18 | 18 | -1 | 0 | 4.5
(6 rows)
Touching edges¶
Visually the edges seem to be connected, but internally they are not.
SELECT id, ST_AsText(geom)
FROM edges where id IN (14,17);
id | st_astext
----+----------------------------------------
17 | LINESTRING(0.5 3.5,1.999999999999 3.5)
14 | LINESTRING(2 3,2 4)
(2 rows)
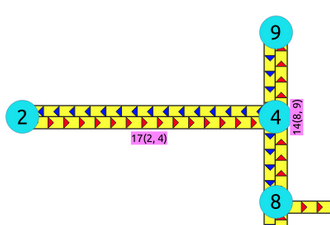
The validity of the information is application dependent.
Maybe there is a small barrier for vehicles but not for pedestrians.
Once analyzed one by one the touchings, for the ones that need a local fix, the edges need to be split.
需要将新边添加到边表中,需要更新新边中的其余属性,需要删除旧边并需要更新路由拓扑。
Fixing a gap¶
In this example the original edge table will be used to store the additional geometries.
An example use without results
Routing from
SELECT *
FROM pgr_dijkstra( 'SELECT id, source, target, cost, reverse_cost FROM edges', 1, 2);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
(0 rows)
Analyze the network for gaps.
WITH
deadends AS (
SELECT id AS vid, (in_edges || out_edges)[1] AS edge, geom AS vgeom
FROM vertices
WHERE array_length(in_edges || out_edges, 1) = 1
)
SELECT id, ST_AsText(geom), vid, ST_AsText(vgeom), ST_Distance(geom, vgeom)
FROM edges, deadends
WHERE id != edge AND ST_Distance(geom, vgeom) < 0.1;
id | st_astext | vid | st_astext | st_distance
----+---------------------+-----+---------------------------+-----------------------
14 | LINESTRING(2 3,2 4) | 4 | POINT(1.999999999999 3.5) | 1.000088900582341e-12
(1 row)
The analysis tell us that the network has a gap.
Prepare tables
Additional columns to control the origin of the segments.
ALTER TABLE edges ADD old_id BIGINT;
ALTER TABLE
Adding new segments.
Calling pgr_separateTouching and adding the new segments to the edges table.
INSERT INTO edges (old_id, geom)
SELECT id, geom
FROM pgr_separateTouching('SELECT id, geom FROM edges');
INSERT 0 2
Update other values
In this example only cost and reverse_cost are updated, where they are
based on the length of the geometry and the directionality is kept using the
sign function.
WITH
costs AS (
SELECT e2.id,
sign(e1.cost) * ST_Length(e2.geom) AS cost,
sign(e1.reverse_cost) * ST_Length(e2.geom) AS reverse_cost
FROM edges e1
JOIN edges e2 ON (e1.id = e2.old_id)
)
UPDATE edges e SET (cost, reverse_cost) = (c.cost, c.reverse_cost)
FROM costs AS c
WHERE e.id = c.id;
UPDATE 2
Update the topology
Insert the new vertices if any.
WITH new_vertex AS (
SELECT ev.*
FROM pgr_extractVertices('SELECT id, geom FROM edges WHERE old_id IS NOT NULL') ev
LEFT JOIN vertices v using(geom)
WHERE v IS NULL
)
INSERT INTO vertices (in_edges, out_edges,x,y,geom)
SELECT in_edges, out_edges,x,y,geom
FROM new_vertex;
INSERT 0 0
Update source and target information on the edges table.
/* -- set the source information */
UPDATE edges AS e
SET source = v.id, x1 = x, y1 = y
FROM vertices AS v
WHERE source IS NULL AND ST_StartPoint(e.geom) = v.geom;
UPDATE 2
/* -- set the target information */
UPDATE edges AS e
SET target = v.id, x2 = x, y2 = y
FROM vertices AS v
WHERE target IS NULL AND ST_EndPoint(e.geom) = v.geom;
UPDATE 2
The example has results
Routing from
SELECT *
FROM pgr_dijkstra('SELECT id, source, target, cost, reverse_cost FROM edges', 1, 2);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 1 | 2 | 1 | 6 | 1 | 0
2 | 2 | 1 | 2 | 3 | 7 | 1 | 1
3 | 3 | 1 | 2 | 7 | 10 | 1 | 2
4 | 4 | 1 | 2 | 8 | 19 | 0.5 | 3
5 | 5 | 1 | 2 | 4 | 17 | 1 | 3.5
6 | 6 | 1 | 2 | 2 | -1 | 0 | 4.5
(6 rows)
连接组件¶
要获取图的连通性:
SELECT * FROM pgr_connectedComponents(
'SELECT id, source, target, cost, reverse_cost FROM edges'
);
seq | component | node
-----+-----------+------
1 | 1 | 1
2 | 1 | 3
3 | 1 | 5
4 | 1 | 6
5 | 1 | 7
6 | 1 | 8
7 | 1 | 9
8 | 1 | 10
9 | 1 | 11
10 | 1 | 12
11 | 1 | 15
12 | 1 | 16
13 | 1 | 17
14 | 2 | 2
15 | 2 | 4
16 | 13 | 13
17 | 13 | 14
(17 rows)
There are three basic ways to connect components:
从顶点到边的起点
从顶点到边的终点
从边上的顶点到最近的顶点
该解决方案需要将边缘分割。
In this example pgr_separateCrossing and pgr_separateTouching will be used.
Get the connectivity
SELECT * FROM pgr_connectedComponents(
'SELECT id, source, target, cost, reverse_cost FROM edges'
);
seq | component | node
-----+-----------+------
1 | 1 | 1
2 | 1 | 3
3 | 1 | 5
4 | 1 | 6
5 | 1 | 7
6 | 1 | 8
7 | 1 | 9
8 | 1 | 10
9 | 1 | 11
10 | 1 | 12
11 | 1 | 15
12 | 1 | 16
13 | 1 | 17
14 | 2 | 2
15 | 2 | 4
16 | 13 | 13
17 | 13 | 14
(17 rows)
Prepare tables
In this example: the edges table will need an additional column and the vertex table will be rebuilt completely.
ALTER TABLE edges ADD old_id BIGINT;
ALTER TABLE
DROP TABLE vertices;
DROP TABLE
Insert new edges
Using pgr_separateCrossing and pgr_separateTouching insert the results into the edges table.
INSERT INTO edges (old_id, geom)
SELECT id, geom FROM pgr_separateCrossing('SELECT * FROM edges')
UNION
SELECT id, geom FROM pgr_separateTouching('SELECT * FROM edges');
INSERT 0 6
创建顶点表
Using pgr_extractVertices create the table.
CREATE TABLE vertices AS
SELECT * FROM pgr_extractVertices('SELECT id, geom FROM edges');
SELECT 18
Update the topology
/* -- set the source information */
UPDATE edges AS e
SET source = v.id, x1 = x, y1 = y
FROM vertices AS v
WHERE ST_StartPoint(e.geom) = v.geom;
UPDATE 24
/* -- set the target information */
UPDATE edges AS e
SET target = v.id, x2 = x, y2 = y
FROM vertices AS v
WHERE ST_EndPoint(e.geom) = v.geom;
UPDATE 24
Update other values
In this example only cost and reverse_cost are updated, where they are
based on the length of the geometry and the directionality is kept using the
sign function.
UPDATE edges e
SET cost = ST_length(e.geom)*sign(e1.cost),
reverse_cost = ST_length(e.geom)*sign(e1.reverse_cost)
FROM edges e1
WHERE e.cost IS NULL AND e1.id = e.old_id;
UPDATE 6
SELECT * FROM pgr_connectedComponents(
'SELECT id, source, target, cost, reverse_cost FROM edges'
);
seq | component | node
-----+-----------+------
1 | 1 | 1
2 | 1 | 2
3 | 1 | 3
4 | 1 | 4
5 | 1 | 5
6 | 1 | 6
7 | 1 | 7
8 | 1 | 8
9 | 1 | 9
10 | 1 | 10
11 | 1 | 11
12 | 1 | 12
13 | 1 | 13
14 | 1 | 14
15 | 1 | 15
16 | 1 | 16
17 | 1 | 17
18 | 1 | 18
(18 rows)
图的收缩¶
可以使用 收缩 - 函数族 来减小图形的大小
何时收缩将取决于图的大小、处理时间、数据的正确性、最终应用程序或任何其他未提及的因素。
确定收缩是否有用的一个相当好的方法是根据死端的数量和/或线性边的数量。
有关如何收缩以及如何使用收缩图的完整方法在 收缩 - 函数族 中进行了描述
死端¶
获取死端:
SELECT id FROM vertices
WHERE array_length(in_edges || out_edges, 1) = 1;
id
----
1
2
5
(3 rows)
死端(Dead End)的形成条件
死端顶点(Dead End Vertex)的拓扑定义。
The vertex is on the limit of the imported graph.
如果导入了更大的图,则该顶点可能不会是死端
节点
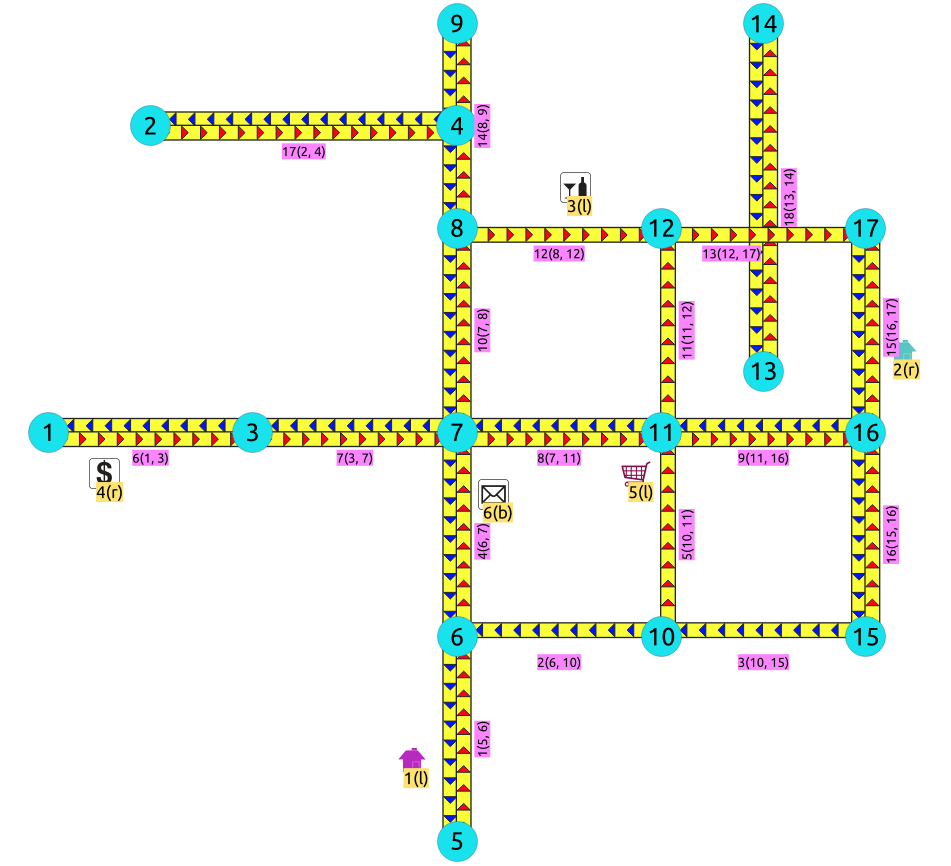
节点
![graph G {
1,2,4,5,9,13,14 [shape=circle;style=filled;color=lightgreen;fontsize=8;width=0.3;fixedsize=true];
3,6,7,8,10,11,12,15,16,17 [shape=circle;style=filled;color=cyan;fontsize=8;width=0.3;fixedsize=true];
5 -- 6 [label="1",fontsize=8]; 6 -- 10 [label="2",fontsize=8];
10 -- 15 [label="3",fontsize=8]; 6 -- 7 [label="4",fontsize=8];
10 -- 11 [label="5",fontsize=8]; 1 -- 3 [label="6",fontsize=8];
3 -- 7 [label="7",fontsize=8]; 7 -- 11 [label="8",fontsize=8];
11 -- 16 [label="9",fontsize=8]; 7 -- 8 [label="10",fontsize=8];
11 -- 12 [label="11",fontsize=8]; 8 -- 12 [label="12",fontsize=8];
12 -- 17 [label="13",fontsize=8]; 8 -- 9 [label="",fontsize=8];
16 -- 17 [label="15",fontsize=8]; 15 -- 16 [label="16",fontsize=8];
2 -- 4 [label="17",fontsize=8]; 13 -- 14 [label="18",fontsize=8];
1 [pos="0,2!"]; 2 [pos="0.5,3.5!"];
3 [pos="1,2!"]; 4 [pos="2,3.5!"];
5 [pos="2,0!"]; 6 [pos="2,1!"];
7 [pos="2,2!"]; 8 [pos="2,3!"];
9 [pos="2,4!"]; 10 [pos="3,1!"];
11 [pos="3,2!"]; 12 [pos="3,3!"];
13 [pos="3.5,2.3!"]; 14 [pos="3.5,4!"];
15 [pos="4,1!"]; 16 [pos="4,2!"];
17 [pos="4,3!"];
}](_images/graphviz-0efc1c6f9c1a1176ac42aaa8de0be1e9186f8539.png)
这个问题的答案将取决于应用情况。
有这么小的路边吗:
这不允许车辆使用该视觉交叉路口?
是否适用于行人,因此行人可以轻松地在小路边行走?
电力和电线的应用是否可以轻松地延伸到小路边顶部?
是否有一个大悬崖,从鹰的角度看,死胡同靠近该路段?
Depending on the answer, modification of the data might be needed.
When there are many dead ends, to speed up processing, the 收缩 - 函数族 functions can be used to contract the graph.
线性边¶
要获得线性边:
SELECT id FROM vertices
WHERE array_length(in_edges || out_edges, 1) = 2;
id
----
3
9
13
15
16
(5 rows)
![graph G {
3,15,17 [shape=circle;style=filled;color=lightgreen;fontsize=8;width=0.3;fixedsize=true];
1,2,4,5,6,7,8,9,10,11,12,13,14,16 [shape=circle;style=filled;color=cyan;fontsize=8;width=0.3;fixedsize=true];
5 -- 6 [label="1",fontsize=8]; 6 -- 10 [label="2",fontsize=8];
10 -- 15 [label="3",fontsize=8]; 6 -- 7 [label="4",fontsize=8];
10 -- 11 [label="5",fontsize=8]; 1 -- 3 [label="6",fontsize=8];
3 -- 7 [label="7",fontsize=8]; 7 -- 11 [label="8",fontsize=8];
11 -- 16 [label="9",fontsize=8]; 7 -- 8 [label="10",fontsize=8];
11 -- 12 [label="11",fontsize=8]; 8 -- 12 [label="12",fontsize=8];
12 -- 17 [label="13",fontsize=8]; 8 -- 9 [label="",fontsize=8];
16 -- 17 [label="15",fontsize=8]; 15 -- 16 [label="16",fontsize=8];
2 -- 4 [label="17",fontsize=8]; 13 -- 14 [label="18",fontsize=8];
1 [pos="0,2!"]; 2 [pos="0.5,3.5!"];
3 [pos="1,2!"]; 4 [pos="2,3.5!"];
5 [pos="2,0!"]; 6 [pos="2,1!"];
7 [pos="2,2!"]; 8 [pos="2,3!"];
9 [pos="2,4!"]; 10 [pos="3,1!"];
11 [pos="3,2!"]; 12 [pos="3,3!"];
13 [pos="3.5,2.3!"]; 14 [pos="3.5,4!"];
15 [pos="4,1!"]; 16 [pos="4,2!"];
17 [pos="4,3!"];
}](_images/graphviz-fcaa0541303f92371c3cf508089a4be8712de558.png)
当这些顶点表示减速带、停止信号,并且应用程序将其纳入考虑时,这些线性顶点是正确的。
When there are many linear vertices, that need not to be taken into account, to speed up the processing, the 收缩 - 函数族 functions can be used to contract the problem.
函数的结构¶
完成上述图准备工作后,就可以使用
pgRouting 函数调用的一般形式是:
pgr_<name>(Inner queries , parameters, [Optional parameters)
其中:
Inner queries :是强制参数,是包含 SQL 查询的
TEXT字符串。parameters:函数需要的附加强制参数。
Optional parameters:是非强制命名参数,省略时具有默认值。
强制参数是位置参数,可选参数是命名参数。
例如,对于这个 pgr_dijkstra` 签名:
pgr_dijkstra(Edges SQL, start vids, end vids, [directed])
-
是第一个参数。
这是强制性的。
这是一个内部查询。
它没有名称,因此 Edges SQL 给出了需要使用哪种内部查询的想法
start vid:
是第二个参数。
这是强制性的。
它没有名称,因此 start vid 给出了第二个参数的值应包含的内容。
end vid
是第三个参数。
这是强制性的。
它没有名称,因此 end vid 给出了第三个参数的值应包含的内容
directed是第四个参数。
是可选的。
它有一个名字。
参数的完整描述可以在每个函数的 Parameters 部分找到。
函数的重载¶
一个函数可能有不同的重载。 最常见的是:
根据过载,参数类型会发生变化。
一: ANY-INTEGER
多:
ARRAY[ANY-INTEGER]
根据函数的不同,重载可能会有所不同。 但参数类型改变的概念保持不变。
一对一¶
当路由来自:
从 一 起始顶点
到 一 结束顶点
一对多¶
当路由来自:
从 一 起始顶点
到 多 结束顶点
多对一¶
当路由来自:
从 多 起始顶点
到 一 结束顶点
多对多¶
当路由来自:
从 多 起始顶点
到 多 结束顶点
组合¶
当路由来自:
从 多个 不同的起始顶点
到 多个 不同的结束顶点
每个元组指定一对起始顶点和结束顶点
用户可以根据需要定义组合。
内部查询¶
有几种有效的内部查询类型,返回的列也取决于函数。哪种类型的内部查询将取决于函数的要求。为了简化类型的种类,使用了 ANY-INTEGER**和**ANY-NUMERICAL。
其中:
- ANY-INTEGER:
SMALLINT, INTEGER, BIGINT
- ANY-NUMERICAL:
SMALLINT, INTEGER, BIGINT, REAL, FLOAT
Edges SQL¶
常规¶
边 SQL
列 |
类型 |
默认 |
描述 |
|---|---|---|---|
|
ANY-INTEGER |
边的标识符。 |
|
|
ANY-INTEGER |
边的第一个端点顶点的标识符。 |
|
|
ANY-INTEGER |
边的第二个端点顶点的标识符。 |
|
|
ANY-NUMERICAL |
边( |
|
|
ANY-NUMERICAL |
-1 |
边(
|
其中:
- ANY-INTEGER:
SMALLINT,INTEGER,BIGINT- ANY-NUMERICAL:
SMALLINT,INTEGER,BIGINT,REAL,FLOAT
一般没有 id¶
边 SQL
列 |
类型 |
默认 |
描述 |
|---|---|---|---|
|
ANY-INTEGER |
边的第一个端点顶点的标识符。 |
|
|
ANY-INTEGER |
边的第二个端点顶点的标识符。 |
|
|
ANY-NUMERICAL |
边( |
|
|
ANY-NUMERICAL |
-1 |
边(
|
其中:
- ANY-INTEGER:
SMALLINT,INTEGER,BIGINT- ANY-NUMERICAL:
SMALLINT,INTEGER,BIGINT,REAL,FLOAT
通常带有(X,Y)¶
边 SQL
参数 |
类型 |
默认 |
描述 |
|---|---|---|---|
|
ANY-INTEGER |
边的标识符。 |
|
|
ANY-INTEGER |
边的第一个端点顶点的标识符。 |
|
|
ANY-INTEGER |
边的第二个端点顶点的标识符。 |
|
|
ANY-NUMERICAL |
边(
|
|
|
ANY-NUMERICAL |
-1 |
边 (
|
|
ANY-NUMERICAL |
|
|
|
ANY-NUMERICAL |
|
|
|
ANY-NUMERICAL |
|
|
|
ANY-NUMERICAL |
|
其中:
- ANY-INTEGER:
SMALLINT,INTEGER,BIGINT- ANY-NUMERICAL:
SMALLINT,INTEGER,BIGINT,REAL,FLOAT
流¶
用于流数据系列 ( Flow - 函数族) 的Edges SQL
边 SQL
列 |
类型 |
默认 |
描述 |
|---|---|---|---|
|
ANY-INTEGER |
边的标识符。 |
|
|
ANY-INTEGER |
边的第一个端点顶点的标识符。 |
|
|
ANY-INTEGER |
边的第二个端点顶点的标识符。 |
|
|
ANY-INTEGER |
边( |
|
|
ANY-INTEGER |
-1 |
边(
|
其中:
- ANY-INTEGER:
SMALLINT,INTEGER,BIGINT- ANY-NUMERICAL:
SMALLINT,INTEGER,BIGINT,REAL,FLOAT
Edges SQL 适用于 Flow - 函数族 的以下函数
列 |
类型 |
默认 |
描述 |
|---|---|---|---|
|
ANY-INTEGER |
边的标识符。 |
|
|
ANY-INTEGER |
边的第一个端点顶点的标识符。 |
|
|
ANY-INTEGER |
边的第二个端点顶点的标识符。 |
|
|
ANY-INTEGER |
边 (
|
|
|
ANY-INTEGER |
-1 |
边 (
|
|
ANY-NUMERICAL |
边 ( |
|
|
ANY-NUMERICAL |
边( |
其中:
- ANY-INTEGER:
SMALLINT,INTEGER,BIGINT- ANY-NUMERICAL:
SMALLINT,INTEGER,BIGINT,REAL,FLOAT
分量 SQL¶
结合签名使用
参数 |
类型 |
描述 |
|---|---|---|
|
ANY-INTEGER |
出发顶点的标识符。 |
|
ANY-INTEGER |
到达顶点的标识符。 |
其中:
- ANY-INTEGER:
SMALLINT,INTEGER,BIGINT
Restrictions SQL¶
列 |
类型 |
描述 |
|---|---|---|
|
|
形成不允许采用的路径的边缘标识符序列。 - 空数组或 |
|
ANY-NUMERICAL |
走禁路的成本。 |
其中:
- ANY-INTEGER:
SMALLINT,INTEGER,BIGINT- ANY-NUMERICAL:
SMALLINT,INTEGER,BIGINT,REAL,FLOAT
Points SQL¶
用于Points SQL
参数 |
类型 |
默认 |
描述 |
|---|---|---|---|
|
ANY-INTEGER |
value |
点的标识符。
|
|
ANY-INTEGER |
距离该点“最近”的边的标识符。 |
|
|
ANY-NUMERICAL |
<0,1> 中的值指示距边缘第一个端点的相对位置。 |
|
|
|
|
[
|
其中:
- ANY-INTEGER:
SMALLINT,INTEGER,BIGINT- ANY-NUMERICAL:
SMALLINT,INTEGER,BIGINT,REAL,FLOAT
参数¶
大多数 pgRouting 函数的主要参数是选择图的边的查询。
参数 |
类型 |
描述 |
|---|---|---|
|
Edges SQL 如下所述。 |
根据函数的族或类别,它将具有附加参数,其中一些是强制性的,一些是可选的。
强制参数是无名的,并且必须按要求的顺序给出。 可选参数是命名参数,并且具有默认值。
Via 函数的参数¶
参数 |
类型 |
默认 |
描述 |
|---|---|---|---|
|
如所述的 SQL 查询。 |
||
via vertices |
|
将要访问的有序顶点标识符数组。 |
|
|
|
|
|
|
|
|
|
|
|
|
|
对于 TRSP 函数¶
列 |
类型 |
描述 |
|---|---|---|
|
如所述的 SQL 查询。 |
|
|
如所述的 SQL 查询。 |
|
|
Combinations SQL 如下所述 |
|
start vid |
ANY-INTEGER |
出发顶点的标识符。 |
start vids |
|
目标顶点的标识符数组。 |
end vid |
ANY-INTEGER |
出发顶点的标识符。 |
end vids |
|
目标顶点的标识符数组。 |
其中:
- ANY-INTEGER:
SMALLINT,INTEGER,BIGINT
结果列¶
根据函数的不同,返回的列有多种。
路径的结果列¶
在返回一个路径解的函数中使用
返回 (seq, path_seq [, start_vid] [, end_vid], node, edge, cost, agg_cost) 的集合
列 |
类型 |
描述 |
|---|---|---|
|
|
从 1 开始的顺序值。 |
|
|
路径中的相对位置。 路径开头的值为 1。 |
|
|
起始顶点的标识符。 当查询中有多个起始向量时返回。 |
|
|
结束顶点的标识符。 当查询中有多个结束顶点时返回。 |
|
|
从 |
|
|
用于从路径序列中的 |
|
|
从使用 |
|
|
从 |
用于以下函数:
返回 (seq, path_seq [, start_pid] [, end_pid], node, edge, cost, agg_cost) 的集合
列 |
类型 |
描述 |
|---|---|---|
|
|
从 1 开始的顺序值。 |
|
|
路径中的相对位置。
|
|
|
路径起始顶点/点的标识符。 |
|
|
路径结束顶点/点的标识符。 |
|
|
从
|
|
|
用于从路径序列中的
|
|
|
从使用
|
|
|
从
|
用于以下函数:
返回 (seq, path_seq, start_vid, end_vid, node, edge, cost, agg_cost)
列 |
类型 |
描述 |
|---|---|---|
|
|
从 1 开始的顺序值。 |
|
|
路径中的相对位置。 路径开头的值为 1。 |
|
|
当前路径起始顶点的标识符。 |
|
|
当前路径结束顶点的标识符。 |
|
|
从 |
|
|
用于从路径序列中的 |
|
|
从使用 |
|
|
从 |
多条路径¶
多路径选择性。¶
这些列取决于函数调用。
(seq, path_id, path_seq [, start_vid] [, end_vid], node, edge, cost, agg_cost) 集合
列 |
类型 |
描述 |
|---|---|---|
|
|
从 1 开始的顺序值。 |
|
|
路径标识符。
|
|
|
路径中的相对位置。 路径开头的值为 1。 |
|
|
起始顶点的标识符。 当查询中有多个起始向量时返回。 |
|
|
结束顶点的标识符。 当查询中有多个结束顶点时返回。 |
|
|
从 |
|
|
用于从路径序列中的 |
|
|
从使用 |
|
|
从 |
多路径非选择性¶
无论调用如何,都会返回所有列。
返回集合``(seq, path_id, path_seq, start_vid, end_vid, node, edge, cost, agg_cost)``
列 |
类型 |
描述 |
|---|---|---|
|
|
从 1 开始的顺序值。 |
|
|
路径标识符。
|
|
|
路径中的相对位置。 路径开头的值为 1。 |
|
|
起始顶点的标识符。 |
|
|
结束顶点的标识符。 |
|
|
从 |
|
|
用于从路径序列中的 |
|
|
从使用 |
|
|
从 |
成本函数结果列¶
用于以下函数
(start_vid, end_vid, agg_cost) 的集合
列 |
类型 |
描述 |
|---|---|---|
|
|
起始顶点的标识符。 |
|
|
结束顶点的标识符。 |
|
|
从 |
Note
当 start_vid 或 end_vid 列具有负值时,标识符用于点。
流量函数的结果列¶
Edges SQL 适用于以下内容
列 |
类型 |
描述 |
|---|---|---|
seq |
|
从 1 开始的顺序值。 |
edge |
|
原始查询中边的标识符 (edges_sql)。 |
start_vid |
|
边的第一个端点顶点的标识符。 |
end_vid |
|
边的第二个端点顶点的标识符。 |
flow |
|
沿 ( |
residual_capacity |
|
( |
Edges SQL 适用于 Flow - 函数族 的以下函数
列 |
类型 |
描述 |
|---|---|---|
seq |
|
从 1 开始的顺序值。 |
edge |
|
原始查询中边的标识符 (edges_sql)。 |
source |
|
边的第一个端点顶点的标识符。 |
target |
|
边的第二个端点顶点的标识符。 |
flow |
|
沿方向 (source, target)流经边缘。 |
residual_capacity |
|
方向 (source, target)上边缘的剩余容量。 |
cost |
|
在方向 (source, target)上通过边缘发送此流的成本。 |
agg_cost |
|
总成本。 |
生成树函数的结果列¶
Edges SQL 适用于以下内容
返回集合 (edge, cost)
列 |
类型 |
描述 |
|---|---|---|
|
|
边的标识符。 |
|
|
穿越边的成本。 |
性能技巧¶
对于路由功能¶
为了获得更快的结果,将查询绑定到路由感兴趣的区域。
在此示例中,使用内部查询 SQL,该 SQL 不包括路由函数中的某些边并且位于结果区域内。
Given this area:
SELECT id, source, target, cost, reverse_cost
FROM edges
WHERE geom && (
SELECT st_buffer(geom, 1) as myarea
FROM edges where id = 6) ORDER BY id;
id | source | target | cost | reverse_cost
----+--------+--------+------+--------------
1 | 5 | 6 | 1 | 1
2 | 6 | 10 | -1 | 1
4 | 6 | 7 | 1 | 1
6 | 1 | 3 | 1 | 1
7 | 3 | 7 | 1 | 1
8 | 7 | 11 | 1 | 1
10 | 7 | 8 | 1 | 1
12 | 8 | 12 | 1 | -1
14 | 8 | 9 | 1 | 1
20 | 8 | 4 | 0.5 | 0.5
(10 rows)
Calculate a route:
SELECT * FROM pgr_dijkstra($$
SELECT id, source, target, cost, reverse_cost
FROM edges
WHERE geom && (
SELECT st_buffer(geom, 1) AS myarea
FROM edges WHERE id = 6)$$,
7, 8);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 7 | 8 | 7 | 10 | 1 | 0
2 | 2 | 7 | 8 | 8 | -1 | 0 | 1
(2 rows)
如何贡献¶
维基
编辑现有的 pgRouting 维基 页面。
或者创建一个新的维基 页面
在 pgRouting 维基 上创建页面
给标题起一个合适的名称
Adding Functionality to pgRouting
查阅`开发者文档 <https://docs.pgrouting.org/doxy/2.4/index.html>`__
索引和表格